2022年山东省平邑九年级中考考前模拟数学试题（含答案）

这是一份2022年山东省平邑九年级中考考前模拟数学试题（含答案），共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

2022年九年级考前模拟数学试题
一、单选题
1．实数的相反数是（     ）
A． B． C． D．
2．观察下列图形，是中心对称图形的是（　　）
A． B． C． D．
3．世界最大的单口径球面射电望远镜被誉为“中国天眼”，在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为0.00519秒．数据0.00519用科学记数法可以表示为（　　）
A．5.19×10﹣3 B．5.19×10﹣4 C．5.19×10﹣5 D．5.19×10﹣6
4．下列计算正确的是（       ）
A．3a+2b=5ab B．(a3)2=a6 C．a6÷a2=a2 D．(a+b)2=a2+b2
5．如图，在平面直角坐标系中，点的坐标为(0，3)，，．将绕点顺时针旋转一定角度后得到，并且点恰好落到线段上，则点的坐标为（       ）

A． B． C． D．
6．将矩形沿折叠，得到如图所示的图形，已知，则的大小是（       ）

A． B． C． D．
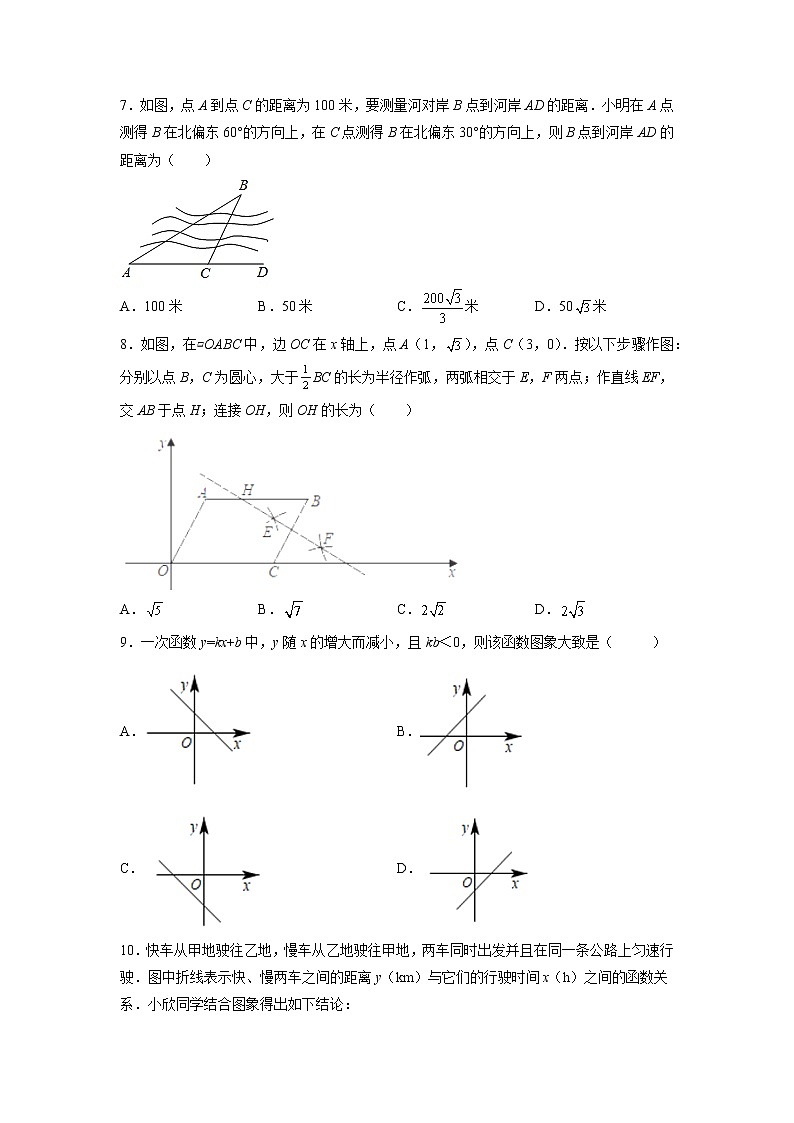
7．如图，点A到点C的距离为100米，要测量河对岸B点到河岸AD的距离．小明在A点测得B在北偏东60°的方向上，在C点测得B在北偏东30°的方向上，则B点到河岸AD的距离为（　　）

A．100米 B．50米 C．米 D．50米
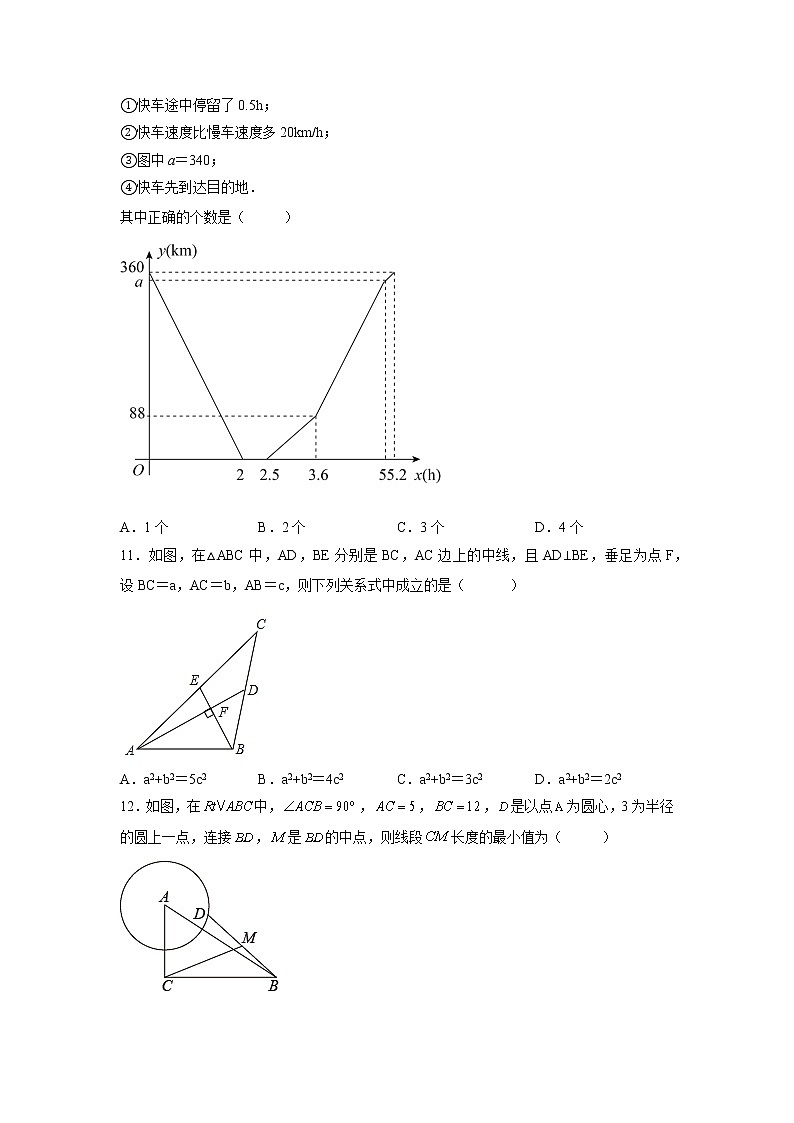
8．如图，在▱OABC中，边OC在x轴上，点A（1，），点C（3，0）．按以下步骤作图：分别以点B，C为圆心，大于BC的长为半径作弧，两弧相交于E，F两点；作直线EF，交AB于点H；连接OH，则OH的长为（　　）

A． B． C． D．
9．一次函数y=kx+b中，y随x的增大而减小，且kb＜0，则该函数图象大致是（       ）
A． B．
C． D．
10．快车从甲地驶往乙地，慢车从乙地驶往甲地，两车同时出发并且在同一条公路上匀速行驶．图中折线表示快、慢两车之间的距离y（km）与它们的行驶时间x（h）之间的函数关系．小欣同学结合图象得出如下结论：
①快车途中停留了0.5h；
②快车速度比慢车速度多20km/h；
③图中a＝340；
④快车先到达目的地．
其中正确的个数是（       ）


A．1个 B．2个 C．3个 D．4个
11．如图，在△ABC中，AD，BE分别是BC，AC边上的中线，且AD⊥BE，垂足为点F，设BC＝a，AC＝b，AB＝c，则下列关系式中成立的是（        ）

A．a2+b2＝5c2 B．a2+b2＝4c2 C．a2+b2＝3c2 D．a2+b2＝2c2
12．如图，在中，，，，是以点为圆心，3为半径的圆上一点，连接，是的中点，则线段长度的最小值为（       ）


A．3 B．4 C．5 D．6
第II卷（非选择题）
请点击修改第II卷的文字说明
二、填空题
13．若一次函数的图象经过第一、二、四象限，则化简________．
14．新冠疫情期间，小李同学连续两周居家健康检测，如图是小李记录的体温情况折线统计图，记第一周体温的方差为，第二周体温的方差为，试判断两者之间的大小关系______．（用“”“”“”填空）

15．图1是一个闭合时的夹子，图2是该夹子的主视示意图，夹子两边为AC，BD（点A与点B重合），点O是夹子转轴位置，OE⊥AC于点E，OF⊥BD于点F，OE=OF=1cm，AC=BD=6cm， CE=DF， CE:AE=2:3.按图示方式用手指按夹子，夹子两边绕点O转动．
(1)当E，F两点的距离最大值时，以点A，B，C，D为顶点的四边形的周长是_____   cm．
(2)当夹子的开口最大（点C与点D重合）时，A，B两点的距离为_____cm．

16．如图，函数(k为常数，k＞0)的图象与过原点的O的直线相交于A，B两点，点M是第一象限内双曲线上的动点（点M在点A的左侧），直线AM分别交x轴，y轴于C，D两点，连接BM分别交x轴，y轴于点E，F．现有以下四个结论：①△ODM与△OCA的面积相等；②若BM⊥AM于点M，则∠MBA＝30°；③若M点的横坐标为1，△OAM为等边三角形，则；④若，则MD＝2MA．其中正确的结论的序号是_______．

三、解答题
17．计算与化简
（1）计算：；
（2）先化简，再求值：，其中a为的小数部分.
18．4张相同的卡片上分别写有数字0、1、、3，将卡片的背面朝上，洗匀后从中任意抽取1张．将卡片上的数字记录下来；再从余下的3张卡片中任意抽取1张，同样将卡片上的数字记录下来．
（1）第一次抽取的卡片上数字是负数的概率为______；
（2）小敏设计了如下游戏规则：当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时，甲获胜：否则，乙获胜．小敏设计的游戏规则公平吗？为什么？（请用画树状图或列表等方法说明理由）．
19．如图，已知是的直径，与相切于C，过点B作，交延长线于点E．

（1）求证：是的平分线；
（2）若，的半径，求的长．
20．戴口罩可以有效降低感染新型冠状病毒的风险．某学校在本学期开学初为九年级学生购买A、B两种口罩，经过市场调查， A的单价比B的单价少2元，花费450元购买A口罩和花费750元购买B口罩的个数相等．
(1)求A、B两种口罩的单价；
(2)若学校需购买两种口罩共500个，总费不超过2100元，求该校本次购买A种口罩最少有多少个?
21．如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象相交于点，与y轴相交于点B．

(1)求点A的坐标及反比例函数的表达式；
(2)点P是反比例函数的图象上一点，连接PA，PB，若的面积为4，求点P的坐标；
(3)在（2）的条件下，取位于A点下方的点P，将线段PA绕点P逆时针旋转90°得到线段PC，连接BC，点M是反比例函数的图象上一点，连接MB，若，求满足条件的点M的坐标．
22．如图，抛物线经过点，点，且．

(1)求抛物线的解析式及其对称轴；
(2)如图，连接，过点作的平行线交抛物线于点，为线段上一动点，连接交抛物线于点，连接交于点，连接，的面积是否有最大值，若有，求出最大值，若无，请说明理由．
(3)如图，以为直角顶点，为直角边边向右作等腰直角，将沿射线线平移得到，连接、，的周长是否有最小值，若有，求的周长的最小值，若无，请说明理由．
23．如图1，在四边形ABCD中，，点E在边BC上，且，，作交线段AE于点F，连接BF．
（1）求证：；
（2）如图2，若，，，求BE的长；
（3）如图3，若BF的延长线经过AD的中点M，求的值．






参考答案：
1．B
【解析】实数的相反数是，
故选：B．
2．C
【解析】A．不是中心对称图形，不符合题意；
B．不是中心对称图形，不符合题意；
C．是中心对称图形，符合题意；
D．不是中心对称图形，不符合题意；
故选C．
3．A
【解析】0.00519＝5.19×10﹣3
故选：A．
4．B
【解析】A、3a+2b≠5ab，无法计算，故此选项错误；
B、(a3)2=a6，故此选项正确；
C、a6÷a2=a4≠a2，故此选项错误；
D、（a+b）2＝a2+2ab+b2≠a2+b2，故此选项错误．
故选：B．
5．D
【解析】过作⊥AO于C点，如图，
∵B(0,3)，
∴OB=3，
∵∠AOB=90°，∠B=30°，
∴∠BAO=60°，
∴在Rt△AOB中，AO=BO×tan∠B=3×tan30°=，
根据旋转的性质可知，
∴△是等边三角形，
∴，
∴在Rt△中，，，
∴，
∵在第二次象限，
∴的坐标为：，
故选：D．

6．B
【解析】由题意可得△ADE≌△ADE ，
∴∠AED = ∠AED，
∵∠CED =60°，
∴∠AED=(180°-60°)=60°，
∴∠AEC =∠AED+ ∠CED =60°+60°=120°
∵矩形 ABCD，
∴AB // CD，
∴∠EAB =180°- ∠AEC =180°-120°=60°．
.故选： B ．
7．D
【解析】过B作BM⊥AD于M，如图：
由题意得：∠BAD＝90°﹣60°＝30°，∠BCD＝90°﹣30°＝60°，
∴∠ABC＝∠BCD﹣∠BAD＝30°，
∴∠BAD＝∠ABC，
∴BC＝AC＝100米，
∵BM⊥AD，
∴∠BMC＝90°，
在Rt△BCM中，sin∠BCM＝，
∴BM＝BC×sin∠BCM＝100×＝50，
即B点到河岸AD的距离为50米，
故选：D．

8．B
【解析】连接HC，过A点作AM⊥x轴于M，如图，

∵OM＝1，，OC＝3，
∴，
∴，
∴∠AOM＝60°，
∵四边形ABCD为平行四边形，
∴∠B＝∠AOM＝60°，BC＝OA＝2，
由作法得EF垂直平分BC，
∴HC＝HB，
∴△HBC为等边三角形，
∴BH＝2，
∴AH＝1，
∴H点的坐标为（2，），
∴．
故选：B．
9．A
【解析】∵一次函数y=kx+b，y随着x的增大而减小，
∴k＜0，
又∵kb＜0，
∴b＞0，
∴图象与y轴的交点在x轴上方，图象经过第一、二、四象限
故选：A．
10．B
【解析】根据题意得，
两车的速度和为：，
相遇后快车停留了，故 ①结论错误；
慢车的速度为：，
则快车的速度为：，
所以快车的速度比慢车多，故②结论正确；
，所以图中，故③结论正确；
快车到达终点的时间为：，
慢车到达终点的时间为：，
因为，所以慢车先到达目的地，故④结论错误，
故选B．
11．A
【解析】设EF＝x，DF＝y，
∵AD，BE分别是BC，AC边上的中线，
∴点F为△ABC的重心，AF＝AC＝b，BD＝a，
∴AF＝2DF＝2y，BF＝2EF＝2x，
∵AD⊥BE，∴∠AFB＝∠AFE＝∠BFD＝90°，
在Rt△AFB中，4x2+4y2＝c2，①
在Rt△AEF中，4x2+y2＝b2，②
在Rt△BFD中，x2+4y2＝a2，③
②+③得5x2+5y2＝（a2+b2），∴4x2+4y2＝（a2+b2），④
①﹣④得c2﹣（a2+b2）＝0，即a2+b2＝5c2．
故选：A．
12．C
【解析】作AB的中点E，连接EM、CE、AD，则有AD=3，


∵∠ACB=90°，
即在中，，
∵E是斜边AB上的中点，
∴，
∵M是BD的中点，E是AB的中点，
∴，
∴在中，，即；
当C、M、E三点共线时有或者；
即，
∴CM最小值为5，
故选：C．
13．
【解析】∵若一次函数y=ax+b的图象经过第一、二、四象限，
∴a＜0，b＞0，
∴b-a＞0，
∴ ，
故答案为-b．
14．
【解析】根据折线统计图很容易看出小丽第一周居家体温在36.6℃～36.8℃之间，第二周居家体温在36.4℃～37.2℃之间，
∵小丽第一周居家体温数值波动小于其第二周居家体温数值波动，
∴S12＜S22．故答案为：＜．
15．     16    
【解析】（1）当E、O、F三点共线时，E、F两点间的距离最大，此时四边形ABCD是矩形，
∴AB=CD=EF=2cm，
∴以点A，B，C，D为顶点的四边形的周长为2+6+2+6=16cm．
（2）当夹子的开口最大（点C与D重合）时，连接OC并延长交AB于点H，

∴，AH=BH，
∵AC=BD=6cm，CE∶AE=2∶3，
∴，
在Rt△OEF中，，
∵，，
∴AB=2AH=．
故答案为16，．
16．①③④
【解析】①设点A（m，），M（n，），
则直线AC的解析式为y=-x++，
∴C（m+n，0），D（0，），
∴，
∴△ODM与△OCA的面积相等，故①正确；
∵反比例函数与正比例函数关于原点对称，
∴O是AB的中点，
∵BM⊥AM，
∴OM=OA，
∴k=mn，
∴A（m，n），M（n，m），
∴，
∴AM不一定等于OM，
∴∠BAM不一定是60°，
∴∠MBA不一定是30°．故②错误，
∵M点的横坐标为1，
∴可以假设M（1，k），
∵△OAM为等边三角形，
∴OA=OM=AM，
1+k2=m2+，
∵m＞0，k＞0，
∴m=k，
∵OM=AM，
∴（1-m）2+(k−)2=1+k2，
∴k2-4k+1=0，
∴k=2±，
∵m＞1，
∴k=2+，故③正确，
如图，作MK∥OD交OA于K．

∵OF∥MK，
∴，
∴，
∵OA=OB，
∴，
∴，
∵KM∥OD，
∴，
∴DM=2AM，故④正确．
故答案为①③④．
17．（1）5；（2）．
【解析】（1）
＝2﹣1+4﹣4×
＝2﹣1+4﹣2+2
＝5；
（2）原式＝


∵a为的小数部分，
∴a＝﹣1，
∴原式＝．
18．（1）；（2）公平，见解析
【解析】（1）共有4种等可能的结果，其中数字是负数情况占1种
P（数字是负数）=；
（2）用树状图或表格列出所有等可能的结果：


∵共有12种等可能的结果，两个数的差为非负数的情况有6种，
∴（结果为非负数），
（结果为负数）．
∴游戏规则公平．
19．（1）见解析；（2）
【解析】（1）∵切与C，
∴，
∵．
∴，
∴，
∴．
∵，
∴，
∴，
∴是的平分线；
（2）在中，
∵，，
∴．
∵，
∴，
∴，
∴．
20．(1)A、B两种型号口罩的单价分别为3元、5元；
(2)该校本次购买A种口罩最少有200个．
【解析】(1)设A种口罩的单价为x元，则B种口罩的单价为（x+2）元，
依题意得：，
解得：x=3，
经检验：x=3是原方程的根，且符合题意，
∴x+2=5．
答：A、B两种型号口罩的单价分别为3元、5元；
(2)设购买A种口罩m个，则购买B种口罩（500-m）个，
依题意得：3m+5（500-m）≤2100，
解得：m≥200．
答：该校本次购买A种口罩最少有200个．
21．(1)（-1，6），
(2)或（-3，2）
(3)（-2，3）或（-6，1）
【解析】(1)将点代入，
得，
解得，，
点的坐标为，
点A代入得，
；
反比例函数；
(2)设点P的坐标为，分情况讨论：
当点P在点A的上方时，如图，过点A作PM//y轴交直线AB于点M，则，

，
，
解得，，（不合题意，舍去）
故点P的坐标为；
当点P在点A的上方时，如图，作的外接矩形PEFG，

，
点E的坐标为，点F的坐标为，点G的坐标为；
，BE＝，FB＝2，AF＝1，，PG＝，
，
，
，

，的面积为4，
，
解得，（不合题意，舍去），
点P的坐标为；
综上，点P的坐标为或（-3，2）
(3)如图，过点P作RS//x轴，过点C，点A作于R，于S，

线段是由绕点逆时针旋转90°得到，
，，
，
，

，
，
，
，
点C到x轴的距离为4，点C到y轴的距离为7，
点C的坐标为（-7，4），
取BC的中点H，过点H作交PC于点N，作直线BN交双曲线于点M，则点M即为所求．
点的坐标为（-3．5，2），NC＝NB，
，

设直线PC的解析式为：
，
，解得，
直线PC的解析式为：，
把代入直线PC得，，
点N的坐标为
设直线BN的解析式为：，
，解得 ，
直线BN的解析式为：，
解方程组，得，
M点的坐标为（-2，3），（-6，1）
22．(1)，对称轴为
(2)有，
(3)有，
【解析】(1)∵OB=OC，C(0,3)，
∴点B(3,0)，即抛物线与x轴交于A(−1,0)，B(3,0)两点，
∴抛物线的表达式为：；
∵C(0,3)，
∴，解得a=-1；
∴ 抛物线的表达式为：，且函数的对称轴为：x=1；
(2)过P作轴，交AH于点Q，如图：

∵C(0,3)，B(3,0)，
∴直线BC解析式为y=−x+3，
∵，
∴设直线AH解析式为，
再将A(−1,0)代入得：0=1+m，解得m=−1，
直线AH解析式为；
由得，，
∴H(4,-5)，
∵，
∴与同底等高，
∴与面积相等，
则有：，
设，根据轴，则有：，
则有：，
∴，
∴代入相应的数值，化简得：，
则有：,
配方得：，
可知当时，有最大值，且最大值为，
(3)连接CE，过F作交y轴于T，如图：

∵沿射线线OD平移得到，
∴，即轴，
∴四边形是平行四边形，
∴CT=EF=OC=3，CE=TF，
∴，
∵等腰直角，，，
∴OC=OB，∠DOC=∠DOB=45°，
又∵OE=OE，
∴，
∴，
∴，
∴，
要使l最小，则有最小，
当T、F、B三点共线时，最小值即是的长度，
而，，
∴，即最小值是，
∴的周长的最小值为．
23．（1）见解析；（2）6；（3）
【解析】（1）证明：，
；
，
，，
，
，，
，，
，，
四边形AFCD是平行四边形


在与中．
，


（2），
，
在中，，
，
，
又，，
，
在与中．
，
；
；
，
；
，
；
，
，
或（舍）；
（3）延长BM、ED交于点G．


与均为等腰三角形，，
，
，
设，，，
则，，
，
，
；
在与中，
，
；
．
；
，
，
，
，
，
，
，
，
（舍），，
．