

所属成套资源:2022年全国各省市初三数学中考真题试卷(含答案)
2022年山东省滨州市初中毕业(学业)考试中考真题数学试卷(含详解)
展开
这是一份2022年山东省滨州市初中毕业(学业)考试中考真题数学试卷(含详解),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年山东省滨州市中考数学试卷
一、选择题:本大题共12个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑.每小题涂对得3分,满分36分.
1.(3分)某市冬季中的一天,中午12时的气温是﹣3℃,经过6小时气温下降了7℃,那么当天18时的气温是( )
A.10℃ B.﹣10℃ C.4℃ D.﹣4℃
2.(3分)在物理学中,导体中的电流I跟导体两端的电压U、导体的电阻R之间有以下关系:I=,去分母得IR=U,那么其变形的依据是( )
A.等式的性质1 B.等式的性质2
C.分式的基本性质 D.不等式的性质2
3.(3分)如图,在弯形管道ABCD中,若AB∥CD,拐角∠ABC=122°,则∠BCD的大小为( )
A.58° B.68° C.78° D.122°
4.(3分)下列计算结果,正确的是( )
A.(a2)3=a5 B.=3 C.=2 D.cos30°=
5.(3分)把不等式组中每个不等式的解集在一条数轴上表示出来,正确的为( )
A.
B.
C.
D.
6.(3分)一元二次方程2x2﹣5x+6=0的根的情况为( )
A.无实数根 B.有两个不等的实数根
C.有两个相等的实数根 D.不能判定
7.(3分)如图,在⊙O中,弦AB、CD相交于点P.若∠A=48°,∠APD=80°,则∠B的大小为( )
A.32° B.42° C.52° D.62°
8.(3分)下列命题,其中是真命题的是( )
A.对角线互相垂直的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形
D.对角线互相垂直的矩形是正方形
9.(3分)在同一平面直角坐标系中,函数y=kx+1与y=﹣(k为常数且k≠0)的图象大致是( )
A. B.
C. D.
10.(3分)今年我国小麦大丰收,农业专家在某种植片区随机抽取了10株小麦,测得其麦穗长(单位:cm)分别为8,8,6,7,9,9,7,8,10,8,那么这一组数据的方差为( )
A.1.5 B.1.4 C.1.3 D.1.2
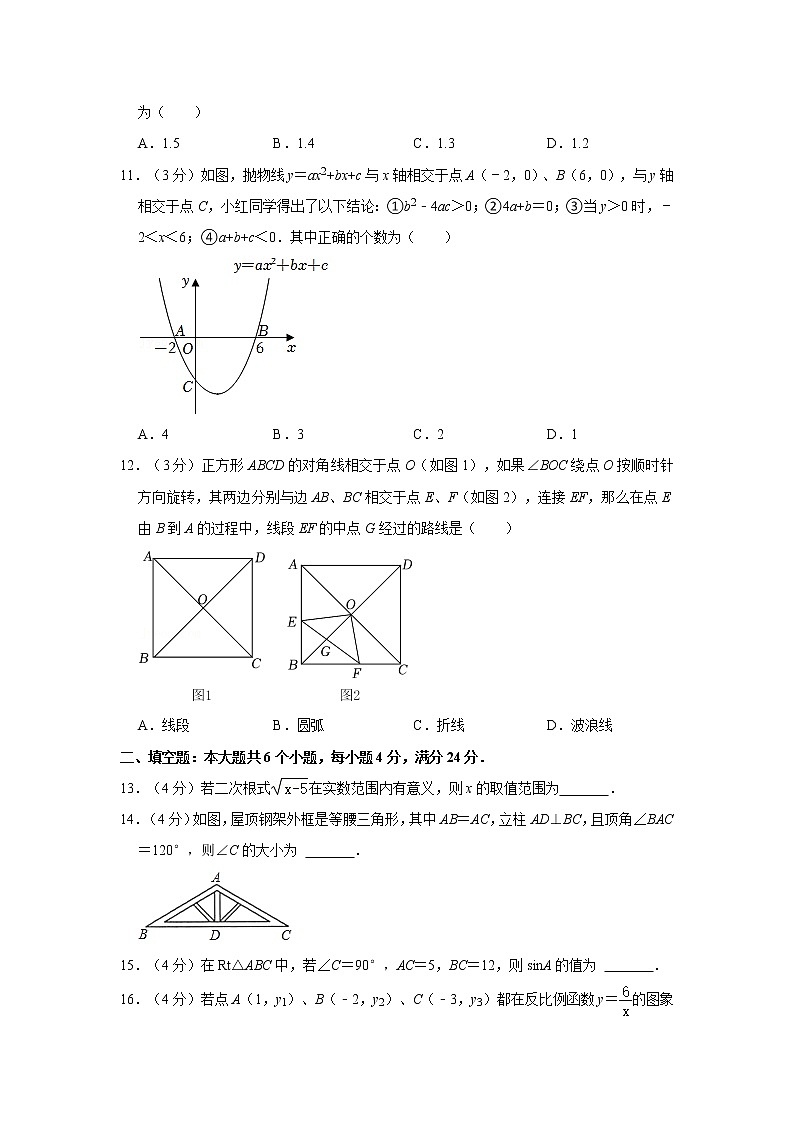
11.(3分)如图,抛物线y=ax2+bx+c与x轴相交于点A(﹣2,0)、B(6,0),与y轴相交于点C,小红同学得出了以下结论:①b2﹣4ac>0;②4a+b=0;③当y>0时,﹣2<x<6;④a+b+c<0.其中正确的个数为( )
A.4 B.3 C.2 D.1
12.(3分)正方形ABCD的对角线相交于点O(如图1),如果∠BOC绕点O按顺时针方向旋转,其两边分别与边AB、BC相交于点E、F(如图2),连接EF,那么在点E由B到A的过程中,线段EF的中点G经过的路线是( )
A.线段 B.圆弧 C.折线 D.波浪线
二、填空题:本大题共6个小题,每小题4分,满分24分.
13.(4分)若二次根式在实数范围内有意义,则x的取值范围为 .
14.(4分)如图,屋顶钢架外框是等腰三角形,其中AB=AC,立柱AD⊥BC,且顶角∠BAC=120°,则∠C的大小为 .
15.(4分)在Rt△ABC中,若∠C=90°,AC=5,BC=12,则sinA的值为 .
16.(4分)若点A(1,y1)、B(﹣2,y2)、C(﹣3,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系为 .
17.(4分)若m+n=10,mn=5,则m2+n2的值为 .
18.(4分)如图,在矩形ABCD中,AB=5,AD=10.若点E是边AD上的一个动点,过点E作EF⊥AC且分别交对角线AC、直线BC于点O、F,则在点E移动的过程中,AF+FE+EC的最小值为 .
三、解答题:本大题共6个小题,满分60分.解答时请写出必要的演推过程.
19.(8分)先化简,再求值:(a+1﹣)÷,其中a=tan45°+()﹣1﹣π0.
20.(9分)某校为满足学生课外活动的需求,准备开设五类运动项目,分别为A:篮球,B:足球,C:乒乓球,D:羽毛球,E:跳绳.为了解学生的报名情况,现随机抽取八年级部分学生进行调查,并根据调查结果绘制了如下两幅不完整的统计图.
请根据以上图文信息回答下列问题:
(1)此次调查共抽取了多少名学生?
(2)请将此条形统计图补充完整;
(3)在此扇形统计图中,项目D所对应的扇形圆心角的大小为 ;
(4)学生小聪和小明各自从以上五类运动项目中任选一项参加活动,请利用画树状图或列表的方法求他俩选择相同项目的概率.
21.(9分)如图,已知AC为⊙O的直径,直线PA与⊙O相切于点A,直线PD经过⊙O上的点B且∠CBD=∠CAB,连接OP交AB于点M.
求证:(1)PD是⊙O的切线;
(2)AM2=OM•PM.
22.(10分)某种商品每件的进价为10元,若每件按20元的价格销售,则每月能卖出360件;若每件按30元的价格销售,则每月能卖出60件.假定每月的销售件数y是销售价格x(单位:元)的一次函数.
(1)求y关于x的一次函数解析式;
(2)当销售价格定为多少元时,每月获得的利润最大?并求此最大利润.
23.(10分)如图,菱形ABCD的边长为10,∠ABC=60°,对角线AC、BD相交于点O,点E在对角线BD上,连接AE,作∠AEF=120°且边EF与直线DC相交于点F.
(1)求菱形ABCD的面积;
(2)求证AE=EF.
24.(14分)如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接AC、BC.
(1)求线段AC的长;
(2)若点P为该抛物线对称轴上的一个动点,当PA=PC时,求点P的坐标;
(3)若点M为该抛物线上的一个动点,当△BCM为直角三角形时,求点M的坐标.
2022年山东省滨州市中考数学试卷
参考答案与试题解析
一、选择题:本大题共12个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑.每小题涂对得3分,满分36分.
1.【解答】解:﹣3﹣7=﹣10(℃),
故选:B.
2.【解答】解:将等式I=,去分母得IR=U,实质上是在等式的两边同时乘R,用到的是等式的基本性质2.
故选:B.
3.【解答】解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=122°,
∴∠BCD=180°﹣122°=58°,
故选:A.
4.【解答】解:A. (a2)=a6,所以A选项不符合题意;
B. ==2,所以B选项不符合题意;
C. =2,所以C选项符合题意;
D.cos30°=,所以D选项不符合题意;
故选:C.
5.【解答】解:解不等式x﹣3<2x,得x>﹣3,
解不等式,得x≤5,
故原不等式组的解集是﹣3<x≤5,
其解集在数轴上表示如下:
故选:C.
6.【解答】解:∵Δ=(﹣5)2﹣4×2×6=25﹣48=﹣23<0,
∴2x2﹣5x+6=0无实数根,
故选:A.
7.【解答】解:∵∠A=∠D,∠A=48°,
∴∠D=48°,
∵∠APD=80°,∠APD=∠B+∠D,
∴∠B=∠APD﹣∠D=80°﹣48°=32°,
故选:A.
8.【解答】解:A、对角线互相垂直的四边形是平行四边形,是假命题,本选项不符合题意;
B、有一个角是直角的四边形是矩形,是假命题,本选项不符合题意;
C、对角线互相平分的四边形是菱形,是假命题,本选项不符合题意;
D、对角线互相垂直的矩形是正方形,是真命题,本选项符合题意.
故选:D.
9.【解答】解:当k>0时,则﹣k<0,一次函数y=kx+1图象经过第一、二、三象限,反比例函数图象在第二、四象限,所以A选项正确,C选项错误;
当k<0时,一次函数y=kx+1图象经过第一、二,四象限,所以B、D选项错误.
故选:A.
10.【解答】解:这一组数据的平均数为×(8+8+6+7+9+9+7+8+10+8)=8,
故这一组数据的方差为×[4×(8﹣8)2+(6﹣8)2+2×(7﹣8)2+2×(9﹣8)2+(10﹣8)2]=1.2,
故选:D.
11.【解答】解:由图象可得,
该抛物线与x轴有两个交点,则b2﹣4ac>0,故①正确;
∵抛物线y=ax2+bx+c与x轴相交于点A(﹣2,0)、B(6,0),
∴该抛物线的对称轴是直线x==2,
∴﹣=2,
∴b+4a=0,故②正确;
由图象可得,当y>0时,x<﹣2或x>6,故③错误;
当x=1时,y=a+b+c<0,故④正确;
故选:B.
12.【解答】解:建立如图平面直角坐标系,设正方形ABCD的边长为1,
∵四边形ABCD是正方形,
∴OAE=∠OBF=45°,OA=OB,
∵∠AOB=∠EOF=90°,
∴∠AOE=∠BOF,
∴△AOE≌△BOF(ASA),
∴AE=BF,
设AE=BF=a,则F(a,0),E(0,1﹣a),
∵EG=FG,
∴G(a,﹣a),
∴点G在直线y=﹣x+上运动,
∴点G的运动轨迹是线段,
故选:A.
二、填空题:本大题共6个小题,每小题4分,满分24分.
13.【解答】解:要使二次根式在实数范围内有意义,必须x﹣5≥0,
解得:x≥5,
故答案为:x≥5.
14.【解答】解:∵AB=AC且∠BAC=120°,
∴∠B=∠C=(180°﹣∠BAC)=×60°=30°.
故答案为:30°.
15.【解答】解:如图所示:∵∠C=90°,AC=5,BC=12,
∴AB==13,
∴sinA=.
故答案为:.
16.【解答】解:∵反比例函数y=,
∴该函数图象在第一、三象限,在每个象限内,y随x的增大而减小,
∵点A(1,y1)、B(﹣2,y2)、C(﹣3,y3)都在反比例函数y=的图象上,
∴y2<y3<0<y1,
即y2<y3<y1,
故答案为:y2<y3<y1.
17.【解答】解:∵m+n=10,mn=5,
∴m2+n2=(m+n)2﹣2mn=102﹣2×5=100﹣10=90.
故答案为:90.
18.【解答】解:如图,过点E作EH⊥BC于点H.
∵四边形ABCD是矩形,
∴∠B=∠BAD=∠BHE=90°,
∴四边形ABHE是矩形,
∴EH=AB=5,
∵BC=AD=10,
∴AC===5,
∵EF⊥AC,
∴∠COF=90°,
∴∠EFH+∠ACB=90°,
∵∠BAC+∠ACB=90°,
∴∠EFH=∠BAC,
∴△EHF∽△CBA,
∴==,
∴==,
∴FH=,EF=,
设BF=x,则DE=10﹣x﹣=﹣x,
∵EF是定值,
∴AF+CE的值最小时,AF+EF+CE的值最小,
∵AF+CE=+,
∴欲求AF+CE的最小值相当于在x轴上找一点P(x,0),使得P到A(0,5),B(,5)的距离和最小,如图1中,
作点A关于x轴的对称点A′,连接BA′交xz轴于点P,连接AP,此时PA+PB的值最小,最小值为线段A′B的长,
∵A′(0,﹣5),B(,5),
∴A′B==,
∴AF+CE的最小值为,
∴AF+EF+CE的最小值为+.
故答案为:+.
三、解答题:本大题共6个小题,满分60分.解答时请写出必要的演推过程.
19.【解答】解:原式=
=•
=•
=,
∵a=tan45°+()﹣1﹣π0
=1+2﹣1
=2,
∴当a=2时,原式==0.
20.【解答】解:(1)10÷10%=100(名),
所以此次调查共抽取了100名学生;
(2)C项目的人数为:100﹣20﹣30﹣15﹣10=25(名),
条形统计图补充为:
(3)在此扇形统计图中,项目D所对应的扇形圆心角为:360°×=54°;
故答案为:54°;
(4)画树状图为:
共有25种等可能的结果,其中相同项目的结果数为5,
所以他俩选择相同项目的概率==.
21.【解答】证明:(1)连接OB,如图所示,
∵OB=OC,
∴∠OCB=∠OBC,
∵AC是⊙O的直径,
∴∠CBA=90°,
∴∠CAB+∠OCB=90°,
∵∠CBD=∠CAB,
∴∠CBD+∠OCB=90°,
∴∠OBD=90°,
∴PD是⊙O的切线;
(2)由(1)知PD是⊙O的切线,直线PA与⊙O相切,
∴PO垂直平分AB,
∴∠AMP=∠ANO=90°,
∴∠APM+∠PAM=90°,
∵∠OAP=90°,
∴∠PAM+∠OAM=90°,
∴∠APM=∠OAM,
∴△OAM∽△APM,
∴,
∴AM2=OM•PM.
22.【解答】解:(1)设y=kx+b,把x=20,y=360,和x=30,y=60代入,可得,
解得:,
∴y=﹣30x+960(10≤x≤32);
(2)设每月所获的利润为W元,
∴W=(﹣30x+960)(x﹣10)
=﹣30(x﹣32)(x﹣10)
=﹣30(x2﹣42x+320)
=﹣30(x﹣21)2+3630.
∴当x=21时,W有最大值,最大值为3630.
23.【解答】(1)解:作AG⊥BC交BC于点G,如图所示,
∵四边形ABCD是菱形,边长为10,∠ABC=60°,
∴BC=10,AG=AB•sin60°=10×=5,
∴菱形ABCD的面积是:BC•AG=10×5=50,
即菱形ABCD的面积是50;
(2)证明:连接EC,
∵四边形ABCD是菱形,∠ABC=60°,
∴EO垂直平分AC,∠BCD=120°,
∴EA=EC,∠DCA=60°,
∴∠EAC=∠ECA,∠ACF=120°,
∵∠AEF=120°,
∴∠EAC+∠EFC=360°﹣∠AEF﹣∠ACF=360°﹣120°﹣120°=120°,
∵∠ECA+∠ECF=120°,
∴∠EFC=∠ECF,
∴EC=EF,
∴AE=EF.
24.【解答】解:(1)针对于抛物线y=x2﹣2x﹣3,
令x=0,则y=﹣3,
∴C(0,﹣3);
令y=0,则x2﹣2x﹣3=0,
∴x=3或x=﹣1,
∵点A在点B的左侧,
∴A(﹣1,0),B(3,0),
∴AC==;
(2)∵抛物线y=x2﹣2x﹣3的对称轴为直线x=﹣=1,
∵点P为该抛物线对称轴上,
∴设P(1,p),
∴PA==,PC==,
∵PA=PC,
∴=,
∴p=﹣1,
∴P(1,﹣1);
(3)由(1)知,B(3,0),C(0,﹣3),
∴OB=OC=3,
设M(m,m2﹣2m﹣3),
∵△BCM为直角三角形,
∴①当∠BCM=90°时,
如图1,过点M作MH⊥y轴于H,则HM=m,
∵OB=OC,
∴∠OCB=∠OBC=45°,
∴∠HCM=90°﹣∠OCB=45°,
∴∠HMC=45°=∠HCM,
∴CH=MH,
∵CH=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,
∴﹣m2+2m=m,
∴m=0(不符合题意,舍去)或m=1,
∴M(1,﹣4);
②当∠CBM=90°时,
过点M作M'H'⊥x轴,
同①的方法得,M'(﹣2,3);
③当∠BMC=90°时,如图2,
过点M作MD⊥y轴于D,过点B作BE⊥DM,交DM的延长线于E,
∴∠CDM=∠E=90°,
∴∠DCM+∠DMC=90°,
∵∠DMC+∠EMB=90°,
∴∠DCM=∠EMB,
∴△CDM∽△MEB,
∴,
∵M(m,m2﹣2m﹣3),B(3,0),C(0,﹣3),
∴DM=m,CD=m2﹣2m﹣3+3=m2﹣2m,ME=3﹣m,BE=﹣(m2﹣2m﹣3)=﹣m2+2m+3,
∴,
∴m=0(舍去)或m=3(点B的横坐标,不符合题意,舍去)或m=(不符合题意,舍去)或m=,
∴M(,﹣),
即满足条件的M的坐标为(1,﹣4)或(﹣2,3)或(,﹣).
声明:试题解析著作权属网所有,未经书面同意,不得复制发布日期:2022/6/16 12:45:24;用户:胡俊波;邮箱:orFmNt1R7QLg1Kha-p-byzLzngWw@weixin.jyeoo.com;学号:28379410
相关试卷
这是一份中考数学真题:2021年陕西省初中毕业学业考试,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份中考数学真题:2018年陕西省初中毕业学业考试,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份中考数学真题:2016年陕西省初中毕业学业考试,共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









