2022年贵州省铜仁市碧江区中考数学模拟试卷 (word版含答案)

这是一份2022年贵州省铜仁市碧江区中考数学模拟试卷 (word版含答案)，共18页。试卷主要包含了5 毫米黑色墨水签字，01×109B，5°，【答案】A，【答案】D，【答案】B等内容，欢迎下载使用。

生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、
姓名是否一致．
2．选择题每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改
动，用橡皮擦干净后，再选涂其他答案标号．非选择题答案用 0.5 毫米黑色墨水签字
笔在答题卡上相应位置书写作答，在试题卷上答题无效．
3．作图可先使用 2B 铅笔画出，确定后必须用 0.5 毫米黑色墨水签字笔描黑．
一、选择题（共15小题，共45分）
当x=-1时，代数式3x+1的值是( )
A. -1B. -2C. 4D. -4
“厉行勤俭节约，反对铺张浪费”势在必行，最新统计数据显示中国每年浪费食物总量折合粮食大约是3010000000人一年的口粮，用科学记数法表示3010000000为( )
A. 3.01×109B. 0.301×109C. 3.1×108D. 301×107
下列各运算中，计算正确的是( )
A. a12÷a3=a4B. (3a2)3=9a6
C. (a-b)2=a2-ab+b2D. 2a⋅3a=6a2
如图是由四个相同的小正方体堆成的物体，它的正视图是( )
A. B.
C. D.
下列长度的三条线段，能组成三角形的是( )
A. 3，4，9B. 5，6，11C. 12，4，6D. 3，4，5
已知一组数据2，3，4，x，1，4，3有唯一的众数4，则这组数据的平均数、中位数分别是( )
A. 4，4B. 3，4C. 4，3D. 3，3
抛物线y=2x2向上平移3个单位，再向右平移2个单位，得到的抛物线是( )
A. y=2(x+2)2-3B. y=2(x+2)2+3
C. y=2(x-2)2-3D. y=2(x-2)2+3
如图，AB//CD，∠A=45°，∠C=∠E，则∠C的度数是( )
A. 30°
B. 22.5°
C. 45°
D. 25°
如图，在平面直角坐标系中，点A是反函数y=kx(k<0,x<0)图象上的点，过点A与x轴垂直的直线交x轴于点B，连结AO，若△ABO的面积为3，则k的值为( )
A. 3
B. -3
C. 6
D. -6
不等式组2x-4≤013xA. B. C. D.
在平面直角坐标系中，点A(6,3)，以原点O为位似中心，在第一象限内把线段OA缩小为原来的13得到线段OC，则点C的坐标为( )
A. (2,1)B. (2,0)C. (3,3)D. (3,1)
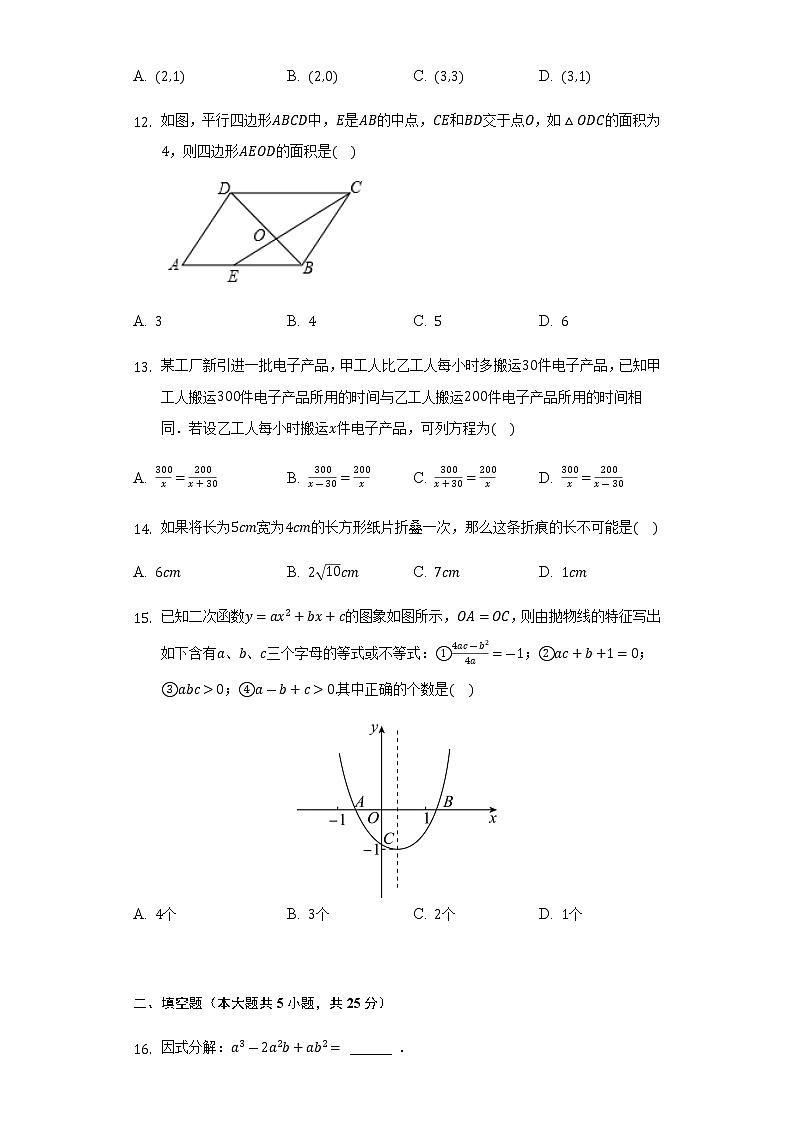
如图，平行四边形ABCD中，E是AB的中点，CE和BD交于点O，如△ODC的面积为4，则四边形AEOD的面积是( )
A. 3B. 4C. 5D. 6
某工厂新引进一批电子产品，甲工人比乙工人每小时多搬运30件电子产品，已知甲工人搬运300件电子产品所用的时间与乙工人搬运200件电子产品所用的时间相同．若设乙工人每小时搬运x件电子产品，可列方程为( )
A. 300x=200x+30B. 300x-30=200xC. 300x+30=200xD. 300x=200x-30
如果将长为5cm宽为4cm的长方形纸片折叠一次，那么这条折痕的长不可能是( )
A. 6cmB. 210cmC. 7cmD. 1cm
已知二次函数y=ax2+bx+c的图象如图所示，OA=OC，则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式：①4ac-b24a=-1；②ac+b+1=0；③abc>0；④a-b+c>0.其中正确的个数是( )
A. 4个B. 3个C. 2个D. 1个
二、填空题（本大题共5小题，共25分）
因式分解：a3-2a2b+ab2= ______ ．
如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，DE是AB的垂直平分线，则∠B的度数是______．
已知关于x的一元二次方程x2-x+m-1=0有两个不相等的实数根，则实数m的取值范围是______．
如图，AB是⊙O的直径，C、D为半圆的三等分点，CE⊥AB于点E，∠ACE的度数为______．
计算：13-22=______．
三、计算题（本大题共2小题，共16分）
计算：2-1+|-5|-sin30°+(π-1)0．
先化简，再求值：(m+2m+1m)÷m+1m2，其中m是方程x2+x-1=0的根．
四、解答题（本大题共5小题，共64分）
为了解某校九年级男生1000米跑的水平，从中随机抽取部分男生进行测试，并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图，请你依图解答下列问题：
(1)a=____，b=____，c=____；
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为____度；
(3)学校决定从A等次的甲、乙、丙、丁四名男生中，随机选取两名男生参加全市中学生1000米跑比赛，请用列表法或画树状图法，求甲、乙两名男生同时被选中的概率．
如图，在▱ABCD中，M，N分别是AD，BC的中点，∠AND=90°，连接CM交DN于点O．
(1)求证：△ABN≌△CDM；
(2)连接MN，求证四边形MNCD是菱形．
某水果销售商发现一种高档水果市场需求量较大，经过市场调查发现月销售量y(箱)与销售单价为x(元/箱)之间的函数关系式为y=-x+800，而这种水果的进价z(元/箱)与进货量y(箱)之间的函数关系式为z=-15y+400(假定：进货量=销售量)，已知每月为此支付员工工资和场地租金等费用总计20000元．
(1)求月获利w(元)与x之间的函数关系式；
(2)当销售单价x为何值时，月获利最大？并求出这个最大值．
如图，已知AB为⊙O的直径，AB⊥AC，BC交⊙O于D，E是AC的中点，ED与AB的延长线相交于点F．
(1)求证：DE为⊙O的切线．
(2)若BF=2，tan∠BDF=12，求⊙O的半径．
已知直线y=-12x+2与x轴、y轴分别交于点A、C，抛物线y=-12x2+bx+c过点A、C，且与x轴交于另一点B，在第一象限的抛物线上任取一点D，分别连接CD、AD，作DE⊥AC于点E．
(1)求抛物线的表达式；
(2)求△ACD面积的最大值；
(3)若△CED与△COB相似，求点D的坐标．
答案和解析
1.【答案】B
【解析】解：把x=-1代入3x+1=-3+1=-2，
故选：B．
把x的值代入解答即可．
此题考查了代数式求值，熟练掌握运算法则是解本题的关键．
2.【答案】A
【解析】解：3010000000=3.01×109．
故选：A．
用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|<10，n为整数，据此判断即可．
此题主要考查了用科学记数法表示较大的数，一般形式为a×10n，其中1≤|a|<10，确定a与n的值是解题的关键．
3.【答案】D
【解析】解：A、原式=a9，不符合题意；
B、原式=27a6，不符合题意；
C、原式=a2-2ab+b2，不符合题意；
D、原式=6a2，符合题意．
故选：D．
各项计算得到结果，即可作出判断．
此题考查了整式的有关运算，熟练掌握运算法则是解本题的关键．
4.【答案】A
【解析】解：从正面看可得从左往右2列正方形的个数依次为2，1，
故选：A．
5.【答案】D
【解析】解：根据三角形任意两边的和大于第三边，得
A中，3+4=7<9，不能组成三角形；
B中，5+6=11，不能组成三角形；
C中，6+4=10<12，不能够组成三角形；
D中，4+3>5，能组成三角形．
故选：D．
6.【答案】D
解：∵这组数据有唯一的众数4，
∴x=4，
将数据从小到大排列为：1，2，3，3，4，4，4，
则平均数=(1+2+3+3+4+4+4)÷7=3，
中位数为：3．
故选：D．
7.【答案】D
【解析】解：抛物线y=2x2向上平移3个单位，再向右平移2个单位，得到的抛物线是y=2(x-2)2+3，
故选：D．
8.【答案】B
【解析】解：∵AB//CD，∠A=45°
∴∠DFE=∠A=45°，
∵∠DFE=∠E+∠C，∠C=∠E
∴∠C=12∠DFE=22.5°
故选：B．
9.【答案】D
【解析】解：∵三角形AOB的面积为3，
∴12|k|=3，
∴|k|=6，
∵k<0，
∴k=-6，
故选：D．
本题考查了反比例函数系数k的几何意义，根据已知条件得到三角形ABO的面积=AB⋅OB，由于三角形ABC的面积=AB⋅OB=3，得到|k|=6，即可得到结论．
10.【答案】C
【解析】解：解不等式2x-4≤0得：x≤2，
解不等式13x1，
不等式组的解集为1不等式组的解集在数轴上表示如下：
故选：C．
求出不等组的解集，将解集在数轴上表示出来即可．
11.【答案】A
解：以原点 O 为位似中心，在第一象限内将其缩小为原来的 13 ，
则点 A 的对应点 C 的坐标为 (6×13,3×13) ，即 (2,1) ，
故选： A ．
12.【答案】C
【解析】解：∵四边形ABCD为平行四边形，
∴CD//BE，CD=AB，
∴△COD∽△EOB，
∴S△CODS△EOB=(CDBE)2．
∵E是AB的中点，
∴AB=2BE，
∴CD=2BE，
∴4S△EOB=22=4，ODOB=2，
∴S△EOB=1，BD=BO+OD=32OD，
∴S△BCD=32S△COD=6．
∵四边形ABCD为平行四边形，
∴S△ABD=S△BCD=6，
∴S四边形AEOD=S△ABD-S△EOB=6-1=5．
故选：C．
根据平行四边形的性质可得出CD//BE、CD=AB，进而可得出△COD∽△EOB，根据
13.【答案】C
【解析】解：设乙工人每小时搬运x件电子产品，则甲每小时搬运(x+30)件电子产品，
依题意得：300x+30=200x
故选：C．
设乙工人每小时搬运x件电子产品，则甲每小时搬运(x+30)件电子产品，根据300÷甲的工效=200÷乙的工效，列出方程．
14.【答案】C
【解析】解：易知最长折痕为矩形对角线的长，根据勾股定理对角线长为：52+42=35≈6.71，
故折痕长不可能为7cm．
故选：C．
根据勾股定理计算出最长折痕即可作出判断．
15.【答案】A
【解析】解：①4ac-b24a=-1，抛物线顶点纵坐标为-1，正确；
②ac+b+1=0，设C(0,c)，则OC=|c|，
∵OA=OC=|c|，∴A(c,0)代入抛物线得ac2+bc+c=0，又c≠0，
∴ac+b+1=0，故正确；
③abc>0，从图象中易知a>0，b<0，c<0，故正确；
④a-b+c>0，当x=-1时y=a-b+c，由图象知(-1,a-b+c)在第二象限，
∴a-b+c>0，故正确．
故选：A．
此题可根据二次函数的性质，结合其图象可知：a>0，-116.【答案】a(a-b)2
解：原式 =a(a2-2ab+b2)
=a(a-b)2 ．
故答案为： a(a-b)2 ．
17.【答案】30°
【解析】解：∵DE是AB的垂直平分线，
∴AD=BD，
∴∠DAB=∠B，
∵AD是∠CAB的平分线，
∴∠CAD=∠DAB，
∵在△ABC中，∠C=90°，
∴3∠B=90°，
∴∠B=30°
故答案为：30°
由在△ABC中，∠C=90°，AD是∠CAB的平分线，DE是AB的垂直平分线，易得∠B=∠DAB=∠CAD，继而求得∠B的度数．
此题考查了线段垂直平分线的性质以及直角三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
18.【答案】m<54
【解答】
解： ∵ 关于 x 的一元二次方程 x2-x+m-1=0 有两个不相等的实数根，
∴△=(-1)2-4×1×(m-1)=5-4m>0 ，
∴m<54 ．
故答案为 m<54 ．
19.【答案】30°
【解析】解：如图，连接OC．
∵AB是直径，AC=CD=BD，
∴∠AOC=∠COD=∠DOB=60°，
∵OA=OC，
∴△AOC是等边三角形，
∴∠A=60°，
∵CE⊥OA，
∴∠AEC=90°，
∴∠ACE=90°-60°=30°．
故答案为30°
20.【答案】-3+225
【解析】解：原式=3+22(3-22)(3+22)
=3+223-8
=-3+225．
故答案为-3+225．
直接分母有理化即可．
本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合并即可．
21.【答案】解：2-1+|-5|-sin30°+(π-1)0．
=12+5-12+1
=6
【解析】先利用负指数，绝对值，特殊角的三角函数，零次幂化简，最后合并即可得出结论．
此题主要考查了负指数，绝对值，特殊角的三角函数，零次幂，熟记性质是解本题的关键．
22.【答案】解：原式=(m2m+2m+1m)⋅m2m+1
=(m+1)2m⋅m2m+1
=m(m+1)
=m2+m，
∵m是方程x2+x-1=0的根，
∴m2+m=1，
则原式=1．
23.【答案】(1)2、45、20；
(2)72；
(3) 画树状图，如图所示：
共有12个可能的结果，选中的两名同学恰好是甲、乙的结果有2个，
故P(选中的两名同学恰好是甲、乙)=212=16．
【解析】
解： (1) 本次调查的总人数为 12÷30%=40 人，
∴a=40×5%=2 ， b=1840×100=45 ， c=840×100=20 ，
故答案为： 2 、 45 、 20 ；
(2) 扇形统计图中表示 C 等次的扇形所对的圆心角的度数为 360°×20%=72° ，
故答案为： 72 ；
(3) 见答案．
【分析】
(1) 根据 A 等次人数及其百分比求得总人数，总人数乘以 D 等次百分比可得 a 的值，再用 B 、 C 等次人数除以总人数可得 b 、 c 的值；
(2) 用 360° 乘以 C 等次百分比可得；
(3) 画出树状图，由概率公式即可得出答案．
此题主要考查了列表法与树状图法，以及扇形统计图、条形统计图的应用，要熟练掌握．
24.【答案】解：
(1)证明：∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，∠B=∠CDM，
∵M、N分别是AD，BC的中点，
∴BN=DM，
∵在△ABN和△CDM中，
AB=CD∠B=∠CDMBN=DM，
∴△ABN≌△CDM(SAS)；
(2)证明：
∵M是AD的中点，∠AND=90°，
∴NM=AM=MD，
∵BN=NC=AM=DM，
∴NC=MN=DM，
∵NCDM，
∴四边形CDMN是平行四边形，
又∵MN=DM，
∴四边形CDMN是菱形．
【解析】(1)由四边形ABCD是平行四边形，可得AB=CD，AD=BC，∠B=∠CDM，又由M、N分别是AD，BC的中点，即可利用SAS证得△ABN≌△CDM；
(2)利用直角三角形形的性质结合菱形的判定方法证明即可．
此题主要考查了平行四边形的性质以及全等三角形的判定与性质、菱形的判定等知识，正确应用直角三角形的性质是解题关键．
25.【答案】解：(1)由题意可得：月获利
w=(x-z)y-20000
=[x-(-15y+400)](-x+800)-20000
=(x-15x-240)(-x+800)
=-45x2+880x-212000；
(2)w=-45x2+880x-212000
=-45(x-550)2+30000，
当销售单价为550元时，月获利最大，最大值为30000元．
26.【答案】(1)证明：连AD，OD，如图所示：
∵AB为⊙O的直径，
∴∠ADB=∠ADC=90°，
∵E是AC的中点，
∴EA=ED，
∴∠EDA=∠EAD，
∵OD=OA，
∴∠ODA=∠OAD，
∴∠EDO=∠EAO，
∵AB⊥AC，
∴∠EAO=90°，
∴∠EDO=90°，
∴DE为⊙O的切线；
(2)解：∵DE为⊙O的切线，
∴∠ODF=∠FDB+∠ODB=∠FAD+∠OBD=90°，
∵OD=OB，
∴∠ODB=∠OBD，
∴∠FDB=∠FAD，
∵tan∠BDF=12，
∴BDAD=12
又∵∠F为公共角，
∴△FDB∽△FAD，
∴BDAD=DFAF=BFDF，
∵BF=2
∴DFAF=2DF
∴DF=4，AF=8
∴AB=8-2=6
∴⊙O的半径是3．
27.【答案】解：(1)∵直线y=-12x+2与x轴、y轴分别交于点A、C，
∴A(4,0)，C(0,2)，OA=4，OC=2，
将A(4,0)，C(0,2)分别代入y=-12x2+bx+c中，
0=-8+4b+c2=c
解得b=32c=2，
∴y=-12x2+32x+2；
(2)如图1，过点D作DG⊥x轴于点G，交AC于点F，
设D(t,-12t2+32t+2)，其中0∴DF=-12t2+32t+2-(-12t+2)=-12t2+2t
S△ACD=S△CDF+S△ADF
=12DF⋅OG+12DF⋅AG
=12DF⋅(OG+AG)
=12DF⋅OA
=12×4×(-12t2+2t)
=-(t-2)2+4．
∴当t=2时，S△ACD最大=4．
(3)设y=0，则-12t2+32t+2=0，
解得x1=4，x2=-1，
∴B(-1,0)，OB=1
∵tan∠OCB=OBOC=12，tan∠OAC=OCOA=24=12
∴∠OCB=∠OAC
∴∠OCA=∠OBC；
①当∠DCE=∠BCO时，∠DCE=∠OAC，
∴CD//OA，点D的纵坐标与点C纵坐标相等，
令y=2，则-12t2+32t+2=2，
解得x1=0，x2=3，
∴D1(3,2)；
②如图2，当∠DCE=∠CBO时，∠DCE=∠OCA，
将△OCA沿AC翻折得△MCA，点O的对称点为点M，
过点M作MH⊥y轴于点H，AN⊥MH于点N，
则CM=CO=2，AM=AO=4，
设HM=m，MN=HN-HM=OA-HM=4-m，
由∠AMC=∠AOC=∠ANM=∠MHC=90°易证△CHM∽△MNA，且相似比CMAM=12，
∴AN=2MH=2m，CH=12MN=2-12m，
在Rt△CMH中，由勾股定理得：m2+(2-12m)2=22，
解得m1=0，m2=85
∴MH=85，OH=165，M(85,165).
设直线CM的表达式为y=kx+n，则2=n165=85k+n，
解得k=34n=2，
∴y=34x+2，
由y=34x+2y=-12x2+32x+2
解得x1=0y1=2，x2=32y2=258
∴D2(32,258)
综上所述，点D的坐标为D1(3,2)、D2(32,258).