2020-2021学年福建省厦门市高二（下）期末数学试卷

这是一份2020-2021学年福建省厦门市高二（下）期末数学试卷，共21页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

2020-2021学年福建省厦门市高二（下）期末数学试卷
一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的。
1．（5分）复数在复平面内对应点的坐标为，则　　
A．3 B．4 C．5 D．6
2．（5分）5人排成一行，其中甲、乙两人相邻的不同排法共有　　
A．24种 B．48种 C．72种 D．120种
3．（5分）的展开式中的系数为　　
A．10 B． C．5 D．
4．（5分）某铁球在时，半径为．当温度在很小的范围内变化时，由于热胀冷缩，铁球的半径会发生变化，且当温度为时铁球的半径为，其中为常数，则在时，铁球体积对温度的瞬时变化率为　　（参考公式：
A．0 B． C． D．
5．（5分）长时间玩手机可能影响视力．据调查，某校学生大约有的人近视，而该校大约有的学生每天玩手机超过1小时，这些人的近视率约为．现从每天玩手机不超过1小时的学生中任意调查一名学生，则他近视的概率约为　　
A．0.125 B．0.25 C．0.375 D．0.4
6．（5分）正四面体中，，分别是，的中点，则直线和夹角的余弦值为　　
A． B． C． D．
7．（5分）如图，一个质点在随机外力的作用下，从原点出发，每次等可能地向左或向右移动一个单位．若质点移动6次，则回到原点的概率为　　

A．0 B． C． D．
8．（5分）已知函数，，若，则的最小值为　　
A． B． C． D．1
二、多选题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多个选项符合题目要求，全部选对的得5分，选对但不全的得2分，有选错的得0分.
9．（5分）随机变量，则　　
A． B．
C． D．
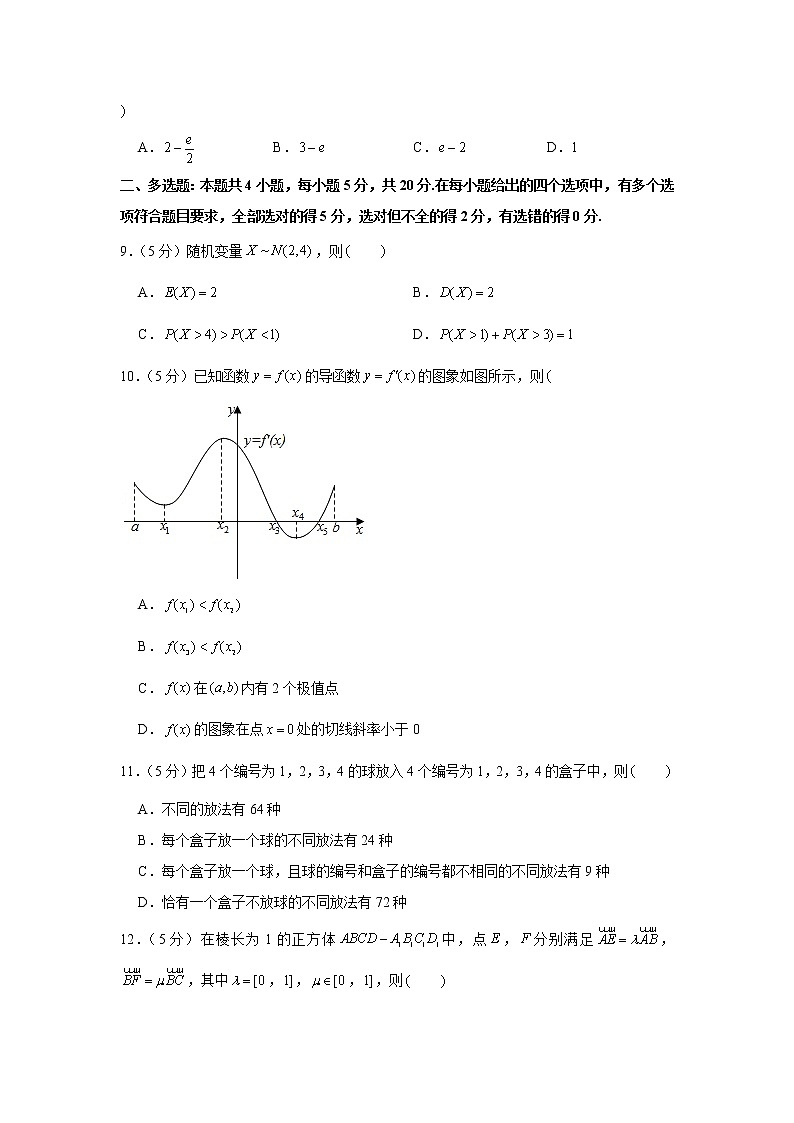
10．（5分）已知函数的导函数的图象如图所示，则

A．
B．
C．在内有2个极值点
D．的图象在点处的切线斜率小于0
11．（5分）把4个编号为1，2，3，4的球放入4个编号为1，2，3，4的盒子中，则　　
A．不同的放法有64种
B．每个盒子放一个球的不同放法有24种
C．每个盒子放一个球，且球的编号和盒子的编号都不相同的不同放法有9种
D．恰有一个盒子不放球的不同放法有72种
12．（5分）在棱长为1的正方体中，点，分别满足，，其中，，，，则　　
A．当时，三棱锥的体积为定值
B．当时，点，到平面的距离相等
C．当时，存在使得平面
D．当时，
三、填空题：本题共4小题，每小题5分，共20分.
13．（5分）若，则　　．
14．（5分）已知，0，，，1，，，0，，若点，1，在平面内，则　　．
15．（5分）由0，1，2，3，4，5组成没有重复数字的三位数，其中偶数有 　　个．（用数字作答）
16．（5分）函数，当时，零点的个数是 　　；若存在实数，使得对于任意，都有，则实数的取值范围是 　　．
四、解答题：本题共6小题，共70分.解答应写出文字说明证明过程或演算步骤.
17．（10分）已知函数在处有极值．
（1）求的解析式；
（2）求在，上的最值．
18．（12分）在国家政策扶持下，近几年我国新能源汽车产业迅速发展．某公司为了解职工购买新能源汽车的意愿，随机调查了30名职工，得到的部分数据如表所示：

愿意
不愿意
合计
男性
15


女性

7
10
合计


30
（1）请将上述列联表补充完整，并判断能否有的把握认为“该公司职工购买新能源汽车的意愿与性别有关”；
（2）为进一步了解职工不愿意购买新能源汽车的原因，从不愿意购买新能源汽车的被调查职工中随机抽取3人进行问卷调查，求至少抽到2名女职工的概率．
附：，其中．

0.100
0.050
0.010
0.001

2.706
3.841
6.635
10.828
19．（12分）如图，在三棱锥中，是正三角形，，是的中点．
（1）证明：；
（2）若，，求二面角的余弦值．

20．（12分）为了解某地区未成年男性身高与体重的关系，对该地区12组不同身高（单位：的未成年男性体重的平均值（单位：，2，，数据作了初步处理，得到下面的散点图和一些统计量的值．







115
24.358
2.958
14300
6300
286
表中，2，，，．
（1）根据散点图判断和哪一个适宜作为该地区未成年男性体重的平均值与身高的回归方程类型？（给出判断即可，不必说明理由）．
（2）根据（1）的判断结果及表中数据，建立关于的回归方程；
（3）如果体重高于相同身高的未成年男性平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么该地区的一位未成年男性身高为，体重为，他的体重是否正常？
附：对于一组数据，，，，，，，其回归直线的斜率和截距的最小二乘估计分别为，，．
21．（12分）一个袋子中有10个大小相同的球，其中有4个白球，6个黄球，从中随机地摸4个球作为样本，用表示样本中黄球的个数，表示样本中黄球的比例．
（1）若有放回摸球，求的分布列及数学期望；
（2）（ⅰ）分别就有放回摸球和不放回摸球，求与总体中黄球的比例之差的绝对值不超过0.2的概率．
（ⅱ）比较（ⅰ）中所求概率的大小，说明其实际含义．
22．（12分）已知函数．
（1）讨论的单调性；
（2）若，求的取值范围．

2020-2021学年福建省厦门市高二（下）期末数学试卷
参考答案与试题解析
一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的。
1．（5分）复数在复平面内对应点的坐标为，则　　
A．3 B．4 C．5 D．6
【解答】解：复数在复平面内对应点的坐标为，则，
所以，
所以．
故选：．
2．（5分）5人排成一行，其中甲、乙两人相邻的不同排法共有　　
A．24种 B．48种 C．72种 D．120种
【解答】解：根据题意，分2步进行分析：
①将甲乙看成一个整体，有种顺序，
②将甲乙整体与其他三人全排列，有种排法，
则有种不同的排法；
故选：．
3．（5分）的展开式中的系数为　　
A．10 B． C．5 D．
【解答】解：的展开式的通项为
令得，
所以展开式中的系数：．
故选：．
4．（5分）某铁球在时，半径为．当温度在很小的范围内变化时，由于热胀冷缩，铁球的半径会发生变化，且当温度为时铁球的半径为，其中为常数，则在时，铁球体积对温度的瞬时变化率为　　（参考公式：
A．0 B． C． D．
【解答】解：根据题意，当温度为时铁球的半径为，其体积，
其导数，
则，即在时，铁球体积对温度的瞬时变化率为，
故选：．
5．（5分）长时间玩手机可能影响视力．据调查，某校学生大约有的人近视，而该校大约有的学生每天玩手机超过1小时，这些人的近视率约为．现从每天玩手机不超过1小时的学生中任意调查一名学生，则他近视的概率约为　　
A．0.125 B．0.25 C．0.375 D．0.4
【解答】解：设该校共有名同学，则约有的学生近视，的学生每天玩手机超过1小时且玩手机超过1小时的学生中有的学生近视．
所以有的学生每天玩手机不超过1小时且其中有的学生近视．
所以从每天玩手机不超过1小时的学生中任意调查一名学生，则他近视的概率约为．
故选：．
6．（5分）正四面体中，，分别是，的中点，则直线和夹角的余弦值为　　
A． B． C． D．
【解答】解连接，取中点，连接，，
设正四面体中棱长为2，
，分别是，的中点，
，是直线和夹角，
，，
，
直线和夹角的余弦值为：
．
故选：．

7．（5分）如图，一个质点在随机外力的作用下，从原点出发，每次等可能地向左或向右移动一个单位．若质点移动6次，则回到原点的概率为　　

A．0 B． C． D．
【解答】解：质点每次移动向左或向右，
设事件为“向右”，则为“向左”，
故，
设表示6次移动中向左移动的次数，
则，
质点回到原点的情况是质点向右和向左各移动3次，
故质点回到原点的概率为．
故选：．
8．（5分）已知函数，，若，则的最小值为　　
A． B． C． D．1
【解答】解：解法一，，
，
，
直线的斜率，
当直线与函数的切线平行时，取得最小值，
设切点为，
令（a），则，则，
（e），即切点为，
函数在切点处的切线方程为，即，令，解得，
令，解得，
．
解法二，
，
，
，
设，，
求导可得，，
当时，函数单调递减，
当时，函数单调递增，
．
的最小值为．
故选：．
二、多选题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多个选项符合题目要求，全部选对的得5分，选对但不全的得2分，有选错的得0分.
9．（5分）随机变量，则　　
A． B．
C． D．
【解答】解：随机变量，
正态分布曲线的对称轴为，即，故选项正确，
标准差为2，则，故选项错误，
由正态分布的对称性可得，，故选项错误，
，
．故选项正确．
故选：．
10．（5分）已知函数的导函数的图象如图所示，则

A．
B．
C．在内有2个极值点
D．的图象在点处的切线斜率小于0
【解答】解：由导函数的图象可知，函数在区间，，， 上均单调递增，故，选项正确，选项错误，
导函数的图象在区间上有两个零点，故原函数有2个极值点，选项正确；
’ ，故的图象在点处的切线斜率大于0，选项错误．
故选：．
11．（5分）把4个编号为1，2，3，4的球放入4个编号为1，2，3，4的盒子中，则　　
A．不同的放法有64种
B．每个盒子放一个球的不同放法有24种
C．每个盒子放一个球，且球的编号和盒子的编号都不相同的不同放法有9种
D．恰有一个盒子不放球的不同放法有72种
【解答】解：根据题意，依次分析选项：
对于，把4个不同的球放入4个不同的盒子中，每个小球有4种放法，则4个小球有中放法，错误；
对于，若每个盒子放一个球，有种放法，正确；
对于，1号球可以放入2、3、4号盒子，有3种放法，剩下3个球有3种放法，则球的编号和盒子的编号都不相同的不同放法有种，正确；
对于，四个不同的小球放入编号为1，2，3，4的四个盒子中，恰有一个空盒，说明恰有一个盒子中有2个小球，
从4个小球中选两个作为一个元素，同另外两个元素在三个位置全排列，故共有种不同的放法，错误；
故选：．
12．（5分）在棱长为1的正方体中，点，分别满足，，其中，，，，则　　
A．当时，三棱锥的体积为定值
B．当时，点，到平面的距离相等
C．当时，存在使得平面
D．当时，
【解答】解：对于，当时，三棱锥的体积等于，因为面，所以到面的距离为定值，可得三棱锥的体积为定值，故正确；
对于，当时，为线段的中点，则点，到平面的距离相等，故正确；
对于，当时，不可能有，则不存在使得平面，故错；
对于，以为原点，、、所在直线分别为轴、轴、轴建立空间直角坐标系，
则，0，、，1，，设，则，，，，1，，
从而，1，，，，，
，，故正确；
故选：．

三、填空题：本题共4小题，每小题5分，共20分.
13．（5分）若，则　2　．
【解答】解：，．
故答案为：2．
14．（5分）已知，0，，，1，，，0，，若点，1，在平面内，则　　．
【解答】解：因为，0，，，1，，，0，，
所以，1，，，0，，
又点，1，在平面内，
所以，其中、；
由，，，
所以，
解得．
故答案为：．
15．（5分）由0，1，2，3，4，5组成没有重复数字的三位数，其中偶数有 　52　个．（用数字作答）
【解答】解：根据题意，若三位数是偶数，则其个位数字必须是2、4或0，
则分2种情况讨论：
1、三位数的个位数字是2或4时，
个位数字有2种情况，0不能在百位，则百位有4种选法，十位数字也有4种选法，
则此时有种情况，
2、三位数的个位数字是0时，
在1、2、3、4、5中任取2个数，安排在百位和十位，有种情况，
则一共可以组成个三位偶数；
故答案为：52．
16．（5分）函数，当时，零点的个数是 　1　；若存在实数，使得对于任意，都有，则实数的取值范围是 　　．
【解答】解：当时，时，单调递增，，故是原函数的零点，当时，．
故只有一个零点0．
再令，，则，
显然当时，，故，
当时，，故此时，故当时，恒有，且当时，取等号；
又，当时，，当时，，故在上单调递减，在上单调递增，且时，取得最小值，
而在上单调递增，同一坐标系内做出与的图像：做出直线，与交于
，易知，当时，方可保证取到最小值，此时时，，时，的下界大于．
故答案为：1，．

四、解答题：本题共6小题，共70分.解答应写出文字说明证明过程或演算步骤.
17．（10分）已知函数在处有极值．
（1）求的解析式；
（2）求在，上的最值．
【解答】解：（1）函数，
则，
因为在处有极值，
所以，即，
解得，，
经检验，，符合题意，
所以；
（2）因为
所以，解得或，
当时，，则单调递增，
当时，，则单调递减，
当时，，则单调递增，
又，，（2），（3），
所以当或时，取得最大值2，
当时，取得最小值．
18．（12分）在国家政策扶持下，近几年我国新能源汽车产业迅速发展．某公司为了解职工购买新能源汽车的意愿，随机调查了30名职工，得到的部分数据如表所示：

愿意
不愿意
合计
男性
15


女性

7
10
合计


30
（1）请将上述列联表补充完整，并判断能否有的把握认为“该公司职工购买新能源汽车的意愿与性别有关”；
（2）为进一步了解职工不愿意购买新能源汽车的原因，从不愿意购买新能源汽车的被调查职工中随机抽取3人进行问卷调查，求至少抽到2名女职工的概率．
附：，其中．

0.100
0.050
0.010
0.001

2.706
3.841
6.635
10.828
【解答】解：（1）根据题意补充列联表为：

愿意
不愿意
合计
男性
15
5
20
女性
3
7
10
合计
18
12
30
由表中数据，计算，
所以没有的把握认为“该公司职工购买新能源汽车的意愿与性别有关”；
（2）不愿意购买新能源汽车的被调查职工中男职工5人，女职工7人，
从这12人中随机抽取3人，至少抽到2名女职工的概率为．
19．（12分）如图，在三棱锥中，是正三角形，，是的中点．
（1）证明：；
（2）若，，求二面角的余弦值．

【解答】解：（1）证明：设的中点为，连，，因为是正三角形，所以，
又因为是的中点，所以，因为，所以，
又因为，
所以平面，
因为平面，所以．
（2）连接，因为，
在中，，
在正中，，因为，所以，所以，又因为，且
，、平面，所以平面，
所以，，两两相互垂直．如图，以为原点，，，所在直线为轴，轴，轴建立空间直角坐标系，则，，，，0，，，0，，，，，所以，1，，，0，，，0，，，，．
设平面的法向量为，，，则，
所以平面的一个法向量为，，．
设平面的法向量为，，，则，
所以平面的一个法向量为，，，
则．
所以二面角的余弦值为．

20．（12分）为了解某地区未成年男性身高与体重的关系，对该地区12组不同身高（单位：的未成年男性体重的平均值（单位：，2，，数据作了初步处理，得到下面的散点图和一些统计量的值．







115
24.358
2.958
14300
6300
286
表中，2，，，．
（1）根据散点图判断和哪一个适宜作为该地区未成年男性体重的平均值与身高的回归方程类型？（给出判断即可，不必说明理由）．
（2）根据（1）的判断结果及表中数据，建立关于的回归方程；
（3）如果体重高于相同身高的未成年男性平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么该地区的一位未成年男性身高为，体重为，他的体重是否正常？
附：对于一组数据，，，，，，，其回归直线的斜率和截距的最小二乘估计分别为，，．
【解答】解：（1）根据散点图，选择模型更适宜作为该地区未成年男性体重的平均值与身高的回归方程类型；
（2）对两边同时取对数，可得，即，
所以，
则，
所以；
（3）由，可得，
令，则，
又，
所以该男生偏胖．
21．（12分）一个袋子中有10个大小相同的球，其中有4个白球，6个黄球，从中随机地摸4个球作为样本，用表示样本中黄球的个数，表示样本中黄球的比例．
（1）若有放回摸球，求的分布列及数学期望；
（2）（ⅰ）分别就有放回摸球和不放回摸球，求与总体中黄球的比例之差的绝对值不超过0.2的概率．
（ⅱ）比较（ⅰ）中所求概率的大小，说明其实际含义．
【解答】解：（1）有放回摸球，每次摸到黄球的概率为，且每次试验之间的结果是独立的，
服从二项分布，即，
的所有可能值为0，1，2，3，4，
，，
，，
，
故的分布列为

0
1
2
3
4






．
（2）样本中黄球的比例为，
由题意，解得，即取2，3，
有放回摸球时，概率，
不放回摸球时，概率．
由可知，，所以在误差不超过0.2的限制下，用样本中黄球比例估计总体黄球比例，采用不放回估计的结果更可靠些．
22．（12分）已知函数．
（1）讨论的单调性；
（2）若，求的取值范围．
【解答】解：（1）函数的定义域为，
，
当时，在上单调递增；
当时，，所以在上恒成立，
所以在上单调递增；
当时，令，解得，
当时，，在上单调递增；
当时，，在上单调递减．
综上所述，当时，在上单调递增；当时，在上单调递增，在上单调递减．
（2），
令，定义域为，因为，
当时，，
令，则在上恒成立，
所以在上单调递增，又，
由零点存在定理可知存在唯一，，使得，
所以当时，；当，时，，
所以在上单调递减，在，上单调递增，
其中，即，



所以在上恒成立．
综上所述，的取值范围为，．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/6/14 16:55:47；用户：13159259195；邮箱：13159259195；学号：39016604