

2020-2021学年河北省石家庄市高二(下)期末数学试卷
展开2020-2021学年河北省石家庄市高二(下)期末数学试卷
一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)复数的实部与虚部之和为
A. B. C. D.
2.(5分)已知函数,是的导函数,则(2)
A.24 B.26 C.32 D.28
3.(5分)函数在,上的平均变化率为
A. B. C.1 D.
4.(5分)展开式中的第3项为
A. B. C.216 D.
5.(5分)某学校高三年级总共有800名学生,学校对高三年级的学生进行一次体能测试.这次体能测试满分为100分,已知测试结果服从正态分布.若在,内取值的概率为0.2,则估计该学校高三年级体能测试成绩在80分以上的人数为
A.160 B.200 C.240 D.320
6.(5分)从1,2,3,4,5,6,7,8中不放回地依次取2个数,事件为“第一次取到的数是偶数”,事件为“第二次取到的数是偶数”,则
A. B. C. D.
7.(5分)已知复数,,且在复平面内对应的点在第一,三象限的角平分线上,则
A. B. C. D.
8.(5分)某学校安排甲、乙,丙、丁、戊五位同学参加数学、物理、化学竞赛,要求每位同学仅报一科,每科至少有一位同学参加,且甲不参加数学竞赛,则不同的安排方法有
A.86种 B.100种 C.112种 D.134种
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.(5分)已知复数,则
A.
B.
C.在复平面内对应的点在第四象限
D.
10.(5分)已知,,则下列结论正确的有
A.若,则 B.若,则
C. D.若,则
11.(5分)下面四个结论中正确的有
A.展开式中各项的二项式系数之和为16
B.用4个0和3个1可以组成35个不同的七位数
C.的展开式中不存在有理项
D.方程有36组正整数解
12.(5分)已知函数,若函数恰有4个零点,则的取值可以是
A. B.3 C.4 D.
三.填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.(5分)若随机变量的分布列为.
0 | 1 | 2 | |
0.3 |
则 .
14.(5分)写出一个恰有1个极值点,且其图象经过坐标原点的函数 .
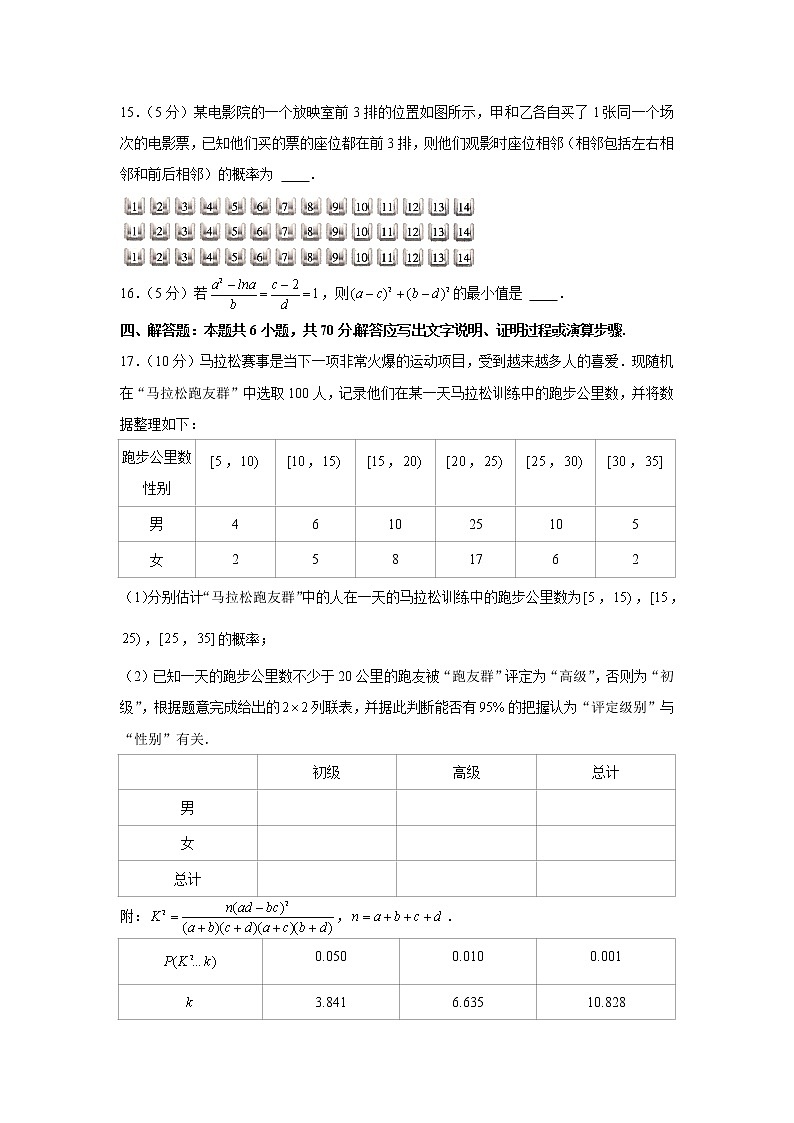
15.(5分)某电影院的一个放映室前3排的位置如图所示,甲和乙各自买了1张同一个场次的电影票,已知他们买的票的座位都在前3排,则他们观影时座位相邻(相邻包括左右相邻和前后相邻)的概率为 .
16.(5分)若,则的最小值是 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)马拉松赛事是当下一项非常火爆的运动项目,受到越来越多人的喜爱.现随机在“马拉松跑友群”中选取100人,记录他们在某一天马拉松训练中的跑步公里数,并将数据整理如下:
跑步公里数 性别 | , | , | , | , | , | , |
男 | 4 | 6 | 10 | 25 | 10 | 5 |
女 | 2 | 5 | 8 | 17 | 6 | 2 |
(1)分别估计“马拉松跑友群”中的人在一天的马拉松训练中的跑步公里数为,,,,,的概率;
(2)已知一天的跑步公里数不少于20公里的跑友被“跑友群”评定为“高级”,否则为“初级”,根据题意完成给出的列联表,并据此判断能否有的把握认为“评定级别”与“性别”有关.
| 初级 | 高级 | 总计 |
男 |
|
|
|
女 |
|
|
|
总计 |
|
|
|
附:,.
0.050 | 0.010 | 0.001 | |
3.841 | 6.635 | 10.828 |
18.(12分)已知函数的导函数是,且(1).
(1)求的解析式;
(2)求经过点且与曲线相切的直线方程.
19.(12分)已知.
(1)求的值;
(2)求的值;
(3)求的值.
20.(12分)某小型企业在开春后前半年的利润情况如表所示:
| 第1个月 | 第2个月 | 第3个月 | 第4个月 | 第5个月 | 第6个月 |
利润(单位:万元) | 4 | 5 | 7 | 14 | 26 | 55 |
设第个月的利润为万元.
(1)根据表中数据,求关于的回归方程(系数精确到;
(2)由(1)中的回归方程预测该企业第7个月的利润是多少万元?(结果精确到整数部分,如98.1万元万元)
(3)已知关于的线性相关系数为0.8834.从相关系数的角度看,与的拟合关系式更
适合用还是,说明你的理由.
参考数据:,,取.
附:样本,,2,,的相关系数,
线性回归方程中的系数,.
21.(12分)在一个不透明的盒中,装有大小、质地相同的两个小球,其中1个是黑色,1个是白色,甲、乙进行取球游戏,两人随机地从盒中各取一球,两球都取出之后再一起放回盒中,这称为一次取球,约定每次取到白球者得1分,取到黑球者得0分,一人比另一人多3分或取满9次时游戏结束,并且只有当一人比另一人多3分时,得分高者才能获得游戏奖品.已知前3次取球后,甲得2分,乙得1分.
(1)求甲获得游戏奖品的概率;
(2)设表示游戏结束时所进行的取球次数,求的分布列及数学期望.
22.(12分)已知函数.
(1)求在,上的单调区间;
(2)设函数,若,,,,求的取值范围.
2020-2021学年河北省石家庄市高二(下)期末数学试卷
参考答案与试题解析
一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)复数的实部与虚部之和为
A. B. C. D.
【解答】解:,
故的实部与虚部之和为.
故选:.
2.(5分)已知函数,是的导函数,则(2)
A.24 B.26 C.32 D.28
【解答】解:,
,
(2).
故选:.
3.(5分)函数在,上的平均变化率为
A. B. C.1 D.
【解答】解:根据题意,在,上的平均变化率,
故选:.
4.(5分)展开式中的第3项为
A. B. C.216 D.
【解答】解:展开式中的第3项为,
故选:.
5.(5分)某学校高三年级总共有800名学生,学校对高三年级的学生进行一次体能测试.这次体能测试满分为100分,已知测试结果服从正态分布.若在,内取值的概率为0.2,则估计该学校高三年级体能测试成绩在80分以上的人数为
A.160 B.200 C.240 D.320
【解答】解:因为测试结果服从正态分布,
所以,
则,
即该学校高三年级体能测试成绩在80分以上的人数估计为.
故选:.
6.(5分)从1,2,3,4,5,6,7,8中不放回地依次取2个数,事件为“第一次取到的数是偶数”,事件为“第二次取到的数是偶数”,则
A. B. C. D.
【解答】解:
.
故选:.
7.(5分)已知复数,,且在复平面内对应的点在第一,三象限的角平分线上,则
A. B. C. D.
【解答】解:
,
在复平面内对应的点在第一、三象限的角平分线上,
,,
.
故选:.
8.(5分)某学校安排甲、乙,丙、丁、戊五位同学参加数学、物理、化学竞赛,要求每位同学仅报一科,每科至少有一位同学参加,且甲不参加数学竞赛,则不同的安排方法有
A.86种 B.100种 C.112种 D.134种
【解答】解:根据题意,分3种情况讨论:
若只有1人参加数学竞赛,有种安排方法;
若恰有2人参加数学竞赛,有种安排方法;
若有3人参加数学竞赛,有种安排方法.
所以共有种安排方法.
故选:.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.(5分)已知复数,则
A.
B.
C.在复平面内对应的点在第四象限
D.
【解答】解:,
在复平面内对应的点在第四象限,
,.
结合选项可知正确,
故选:.
10.(5分)已知,,则下列结论正确的有
A.若,则 B.若,则
C. D.若,则
【解答】解:,,
若,则,,故选项错误,选项正确,
,,故选项正确,
,,
化简整理可得,解得,故选项正确.
故选:.
11.(5分)下面四个结论中正确的有
A.展开式中各项的二项式系数之和为16
B.用4个0和3个1可以组成35个不同的七位数
C.的展开式中不存在有理项
D.方程有36组正整数解
【解答】解:展开式中各项的二项式系数之和为,故正确.
用4个0和3个1可以组成个不同的七位数,故错误.
因为,
所以展开式中的第5项为常数项,故错误.
方程正整数解的组数等价于问题:10瓶相同的矿泉水分给3个人,每人至少分得1瓶,共有
多少种不同的分法?
所以此问题可以用隔板法解决,将10瓶相同的矿泉水排成一排,中间有9个空,
选取两个空插入两块隔板,则不同分法数为,故正确.
故选:.
12.(5分)已知函数,若函数恰有4个零点,则的取值可以是
A. B.3 C.4 D.
【解答】解:因为的零点为,
所以由,
得或,即或.
因为,
所以在上单调递增,在上单调递减,
则的极大值为,极小值为,
因为,
所以,
结合的图象可得,解得.
故选:.
三.填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.(5分)若随机变量的分布列为.
0 | 1 | 2 | |
0.3 |
则 0.25 .
【解答】解:,
.
故答案为:0.25.
14.(5分)写出一个恰有1个极值点,且其图象经过坐标原点的函数 (答案不唯一) .
【解答】解:令(答案不唯一),
则,且恰有1个极值点,
故答案为:(答案不唯一).
15.(5分)某电影院的一个放映室前3排的位置如图所示,甲和乙各自买了1张同一个场次的电影票,已知他们买的票的座位都在前3排,则他们观影时座位相邻(相邻包括左右相邻和前后相邻)的概率为 .
【解答】解:若他们的座位左右相邻,则有种可能;若他们的座位前后相邻,则有种可能.
所以他们观影时座位相邻的概率.
故答案为:.
16.(5分)若,则的最小值是 2 .
【解答】解:由,
得,,
则问题转化为曲线上的点与直线上的点之间的距离平方的最小值,
利用切线以及平行线间的距离公式计算即可,
令,设曲线上一点,,
在点处的切线斜率为,
依题意,得,解得,或(舍去),
所以,
函数图象在点处的切线方程为,又,
所以切线方程为,
直线方程为,
由平行线间的距离公式,得,
所以的最小值为2.
故答案为:2.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)马拉松赛事是当下一项非常火爆的运动项目,受到越来越多人的喜爱.现随机在“马拉松跑友群”中选取100人,记录他们在某一天马拉松训练中的跑步公里数,并将数据整理如下:
跑步公里数 性别 | , | , | , | , | , | , |
男 | 4 | 6 | 10 | 25 | 10 | 5 |
女 | 2 | 5 | 8 | 17 | 6 | 2 |
(1)分别估计“马拉松跑友群”中的人在一天的马拉松训练中的跑步公里数为,,,,,的概率;
(2)已知一天的跑步公里数不少于20公里的跑友被“跑友群”评定为“高级”,否则为“初级”,根据题意完成给出的列联表,并据此判断能否有的把握认为“评定级别”与“性别”有关.
| 初级 | 高级 | 总计 |
男 |
|
|
|
女 |
|
|
|
总计 |
|
|
|
附:,.
0.050 | 0.010 | 0.001 | |
3.841 | 6.635 | 10.828 |
【解答】解:(1)由频数分布表可知,估计“马拉松跑友群”中的人在一天的马拉松训练中的跑步公里数为,的概率为,
跑步公里数为,的概率为,跑步公里数为,的概率为;
(2)列联表如下:
| 初级 | 高级 | 总计 |
男 | 20 | 40 | 60 |
女 | 15 | 25 | 40 |
总计 | 35 | 65 | 100 |
因为,
所以没有的把握认为“评定级别”与“性别”有关.
18.(12分)已知函数的导函数是,且(1).
(1)求的解析式;
(2)求经过点且与曲线相切的直线方程.
【解答】解:(1)由(1),得(1)(1),
,解得,
;
(2)设该切线的切点坐标为,
,
该切线方程为.
将代入方程,整理得,解得
当时,切线方程为;
当时,切线方程为.
综上,经过点且与曲线相切的直线方程为或.
19.(12分)已知.
(1)求的值;
(2)求的值;
(3)求的值.
【解答】解:(1)因为,
所以,
所以
(2)令,得.
令,得,
又,
所以,,.
(3)由题可知,,
,,
所以.
20.(12分)某小型企业在开春后前半年的利润情况如表所示:
| 第1个月 | 第2个月 | 第3个月 | 第4个月 | 第5个月 | 第6个月 |
利润(单位:万元) | 4 | 5 | 7 | 14 | 26 | 55 |
设第个月的利润为万元.
(1)根据表中数据,求关于的回归方程(系数精确到;
(2)由(1)中的回归方程预测该企业第7个月的利润是多少万元?(结果精确到整数部分,如98.1万元万元)
(3)已知关于的线性相关系数为0.8834.从相关系数的角度看,与的拟合关系式更
适合用还是,说明你的理由.
参考数据:,,取.
附:样本,,2,,的相关系数,
线性回归方程中的系数,.
【解答】解:(1)关于的回归方程,
设,,
则,
所以,
故关于的回归方程为.
(2)当时,,
故可预测第7个月的利润约为114万元.
(3)由(1)知,关于的线性相关系数
,
因为,
所以与的拟合关系式更适合用.
21.(12分)在一个不透明的盒中,装有大小、质地相同的两个小球,其中1个是黑色,1个是白色,甲、乙进行取球游戏,两人随机地从盒中各取一球,两球都取出之后再一起放回盒中,这称为一次取球,约定每次取到白球者得1分,取到黑球者得0分,一人比另一人多3分或取满9次时游戏结束,并且只有当一人比另一人多3分时,得分高者才能获得游戏奖品.已知前3次取球后,甲得2分,乙得1分.
(1)求甲获得游戏奖品的概率;
(2)设表示游戏结束时所进行的取球次数,求的分布列及数学期望.
【解答】解:(1)设甲获得游戏奖品为事件,
所以甲获得游戏奖品的概率为;
(2)可能的取值为:5,7,9;,,,
的分布列为
5 | 7 | 9 | |
的数学期望.
22.(12分)已知函数.
(1)求在,上的单调区间;
(2)设函数,若,,,,求的取值范围.
【解答】解:(1),
当,时,,函数在,上的零点为,
当时,;
当时,;
当时,;
当时,.
故在,上的单调递增区间为
单调递减区间为.
(2)由(1)知,在,上的最大值为.
当时,
设函数,
则
当时,;
当时,.
故
设函数,
因为,
所以.
所以当时,,
因为,,,,
所以,
故,即的取值范围是.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2022/6/14 16:47:56;用户:13159259195;邮箱:13159259195;学号:39016604
2022-2023学年河北省石家庄市高二(上)期末数学试卷: 这是一份2022-2023学年河北省石家庄市高二(上)期末数学试卷,共21页。试卷主要包含了单选题,多项选择题,填空题,解答题等内容,欢迎下载使用。
河北省石家庄市2020-2021学年高二下学期期末联考 数学试题: 这是一份河北省石家庄市2020-2021学年高二下学期期末联考 数学试题,共13页。试卷主要包含了 已知复数,则, 已知,则下列结论正确的有等内容,欢迎下载使用。
2022-2023学年河北省石家庄市高二(下)期末数学试卷(含解析): 这是一份2022-2023学年河北省石家庄市高二(下)期末数学试卷(含解析),共20页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












