








初中数学人教版七年级上册1.2.4 绝对值教学ppt课件
展开1. 课前预热2. 导入新课3. 绝对值的概念4. 典例解析5. 当堂小测6. 课堂小结7. 课后练习
教学重点:理解绝对值概念,借助数轴理解几何意义
教学难点:掌握一个数的绝对值求法和性质,利用绝对值解决实际问题,进一步了解数形结合思想
教学目标:理解绝对值概念,借助数轴理解几何意义,掌握一个数的绝对值求法和性质,利用绝对值解决实际问题,进一步了解数形结合思想
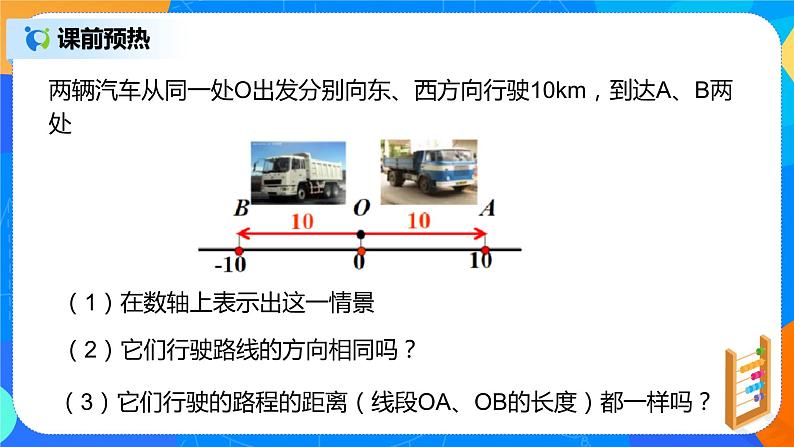
两辆汽车从同一处O出发分别向东、西方向行驶10km,到达A、B两处
(2)它们行驶路线的方向相同吗?
(3)它们行驶的路程的距离(线段OA、OB的长度)都一样吗?
(1)在数轴上表示出这一情景
解:路程一样,到原点的距离相等(不管方向),OA=OB
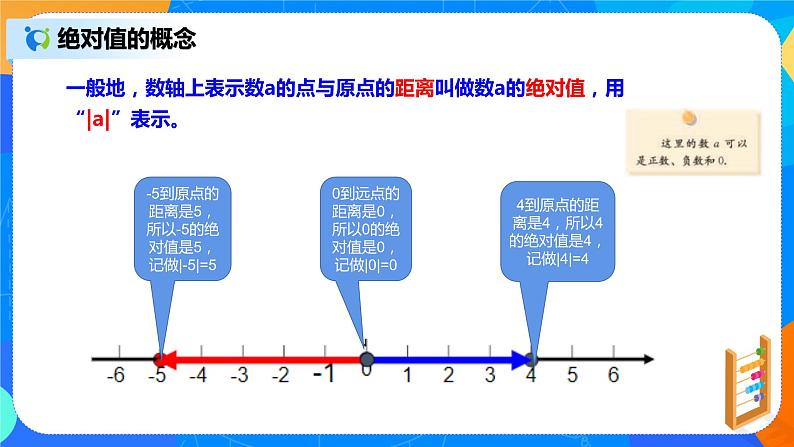
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,用“|a|”表示。
-5到原点的距离是5,所以-5的绝对值是5,记做|-5|=5
0到远点的距离是0,所以0的绝对值是0,记做|0|=0
4到原点的距离是4,所以4的绝对值是4,记做|4|=4
想一想:一个正数的绝对值是什么?一个负数的绝对值是什么?0的绝对值是什么?
|-3.9|=3.9,
例2.若|a﹣1|=a﹣1,则 a 的取值范围是()A. a≥1B. a≤1C. a<1D. a>1
解:观察发现绝对值等于a-1本身,所以可知绝对值里面 不是一个负数即非负数,所以a-1≥0,所以a≥1
归纳:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.
即:(1)如果a>0,那么|a|=_____
(2)如果a=0,那么|a|=____
(3)如果a<0,那么|a|=_____
思考:相反数和绝对值有什么联系?
|-5|= |+5|=
互为相反数的两个数的绝对值相等
绝对值相等,符号相反的两个数互为相反数
绝对值相等的两个数可能相等或也可能互为相反数!
解:(1)-(-5)=5 -|-5|=-5 所以-(-5)>-|-5|
(2)-(+3)=-3 所以-(+3)<0
(4)-|-3.14|=-3.14 |-π|>|-3.14|(即-π在负半轴离原点更远)所以-π<-|-3.14|
归纳:1.比较之前先化简,负数小于正数,负数小于0.
2.同号比较 同正号:绝对值大的正数越大。
同负号:绝对值大的负数越小。
含有字母的绝对值的化简
例4.把下列各式去掉绝对值的符号.(1)|a-4|(a≥4);(2)|5-b|(b>5).
解:(1)因为a-4≥0 所以|a-4|=a-4
(2)5-b<0 所以|5-b|=-(5-b)-5+b
注意:绝对值里面不是一个数或字母时要把绝对值符号里面看成一个整体,求整体的相反数注意带括号!
例5.已知有理数 a,b,c 在数轴上对应的点的位置如图所示:化简:|a-b|+|c-b|+|2b-c|
解:因为a<b,所以a-b<0,所以|a-b|=-(a-b) 同理c<b,所以c-b<,所以|c-b|=-(c-b) 因为b>c,所以2b-c>0,所以|2b-c|=2b-c 所以原式=-(a-b)-(c-b)+2b-c =-a+b-c+b+2b-c =-a+4b-2c
解:因为|a|≥0,正数+正数≠0,所以原式只能理解成|0|+|0|=0 所以a+1=0,2-b=0,所以a=-1,b=2
例7:(1)设x为一个有理数,若|x|=x,则x必定是( )A.负数 B.正数 C.非负数 D.零
(2)如果一个数的绝对值等于它的相反数,那么这个数一定是( )A.正数 B.负数 C.正数或零 D.负数或零
一个数的绝对值等于它本身,则这个数为非负数,即|a|=a(a≥0)一个数的绝对值等于它的相反数,则这个数为非正数,即|a|=-a(a≤0)
解:原式子理解成绝对值等于本身,正数和0满足。
解:容易想到负数绝对值,注意0的相反数还是0.
例8:正式足球比赛对所用足球的质量有严格的规定,下面是 6 个足球的质量检测结果,用正数记超过规定质量的克数,用负数记不足规定质量的克数.检测结果(单位:克):-25,+10,-20,+30,+15,-40.裁判员应该选择哪个足球用于这场比赛呢?请说明理由.
解:|-25|=25,|+10|=10,|-20|=20,|+30|=30,|+15|=15,|-40|=40. +10的绝对值最小,误差最小最接近标准质量所以应该选择克数为+10的那一个
1.如果数轴上的点 A 到原点的距离是 6,则点 A 表示的数为_____. 如果|x-2|=1,那么 x=_________; 如果|x|>3,那么 x的范围是 _________.
3.若|x﹣5|=5﹣x,下列不等式成立的是()A. x﹣5>0B. x﹣5<0C. x﹣5≥0D. x﹣5≤0
4.满足|x|=-x 的数有()A.1 个B.2 个C.3 个D.无数个
5.如图,数轴上的三点A,B,C分别表示有理数a,b,c,化简|a﹣b|﹣|a+c|+|b﹣c|.
解:看数轴可知a<b,所以a-b<0,所以|a-b|=-(a-b) a<0,c>0,|a|>|c|,所以a+c<0,所以|a+c|=-(a+c) b<c,所以b-c<0,所以|b-c|=-(b-c) 所以原式=-(a-b)-[-(a+c)]+[-(b-c)] =-a+b+(a+c)-(b-c) =-a+b+a+c-b+c =2c
6. 一只可爱的小虫从点O出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,小虫爬行的各段路程(单位:cm)依次记为:+5,-3,+10,-8,-6,+12,-10,在爬行过程中,如果小虫每爬行1cm就奖励2粒芝麻,那么小虫一共可以得到多少粒芝麻?
解:依题意得|+5|+|-3|+|+10|+|-8|+|-6|+|+12|+|-10| =5+3+10+8+6+12+10 =54(cm) 54×2=108(粒) 所以小虫一共可以得到108粒芝麻。
1.如图,数 O是原点,A、B、C三点所表示的数分别为 a、b、c.根据图中各点的位置, 下列各数的绝对值的比较何者正确?()A.|b|<|c|B.|b|>|c|C.|a|<|b|D.|a|>|c|
2.a、b 为有理数,且 a>0、b<0,|b|>a,则 a、b、-a、-b 的大小顺序是() A.b<-a<a<-bB.-a<b<a<-bC.-b<a<-a<bD.-a<a<-b<b
3.下列推理:①若 a=b,则|a|=|b|;②若|a|=|b|,则 a=b;③若 a≠b, 则|a|≠|b|;④若|a|≠|b|,则 a≠b.其中正确的个数为()A.4 个B.3 个C.2 个D.1 个
4.式子|2x-1|+2 取最小值时,x 等于_______.
6.数 a 在数轴上的位置如图所示,则|a-2|=_______.
解:因为a处于分母的位置所以不能为0
7.正式的足球比赛对所用足球的质量都有严格的规定,标准质量为 400 克.下面是 5 个足球的质量检测结果(超过规定质量的克数记为正数,不足规定质量的克数记为负数):-25,+10,-20,+30,+15.(1)写出每个足球的质量;(2)请指出哪个足球的质量好一些,并用绝对值的知识进行说明.
解:(1)5个足球的质量分别是:375克,410克,380克,430克,415克
(2)|-25|=25,|+10|=10,|-20|=20,|+30|=30,|+15|=15|+10|绝对值的数最小,即误差最小最接近标准质量所以420克的足球质量好一些。
初中数学人教版七年级上册1.2.4 绝对值说课ppt课件: 这是一份初中数学人教版七年级上册1.2.4 绝对值说课ppt课件,共12页。PPT课件主要包含了学前温故,新课早知等内容,欢迎下载使用。
七年级上册1.2.4 绝对值教学演示ppt课件: 这是一份七年级上册1.2.4 绝对值教学演示ppt课件,共30页。PPT课件主要包含了做一做,想一想,课堂升华,试一试等内容,欢迎下载使用。
初中数学人教版七年级上册1.2.4 绝对值课前预习ppt课件: 这是一份初中数学人教版七年级上册1.2.4 绝对值课前预习ppt课件,共11页。PPT课件主要包含了绝对值的意义的学习,有理数的大小比较,例题1,绝对值的非负性,例题2,即a1b2,又c0d-1,绝对值的拓展应用,例题3,-a+2b-c等内容,欢迎下载使用。














