2022年江苏省盐城市亭湖区、盐都区、阜宁县、大丰区中考数学二模试卷（含解析）

这是一份2022年江苏省盐城市亭湖区、盐都区、阜宁县、大丰区中考数学二模试卷（含解析），共26页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
2022年江苏省盐城市亭湖区、盐都区、阜宁县、大丰区中考数学二模试卷

题号
一
二
三
四
总分
得分






一、选择题（本大题共8小题，共24分）
1. 实数−2022是2022的(    )
A. 绝对值 B. 相反数 C. 倒数 D. 以上都不正确
2. “疫情就是命令，防控就是责任”，面对疫情，各地积极普及科学防控知识．下面是科学防控知识图片，其中图案是轴对称图形的是(    )
A. B. C. D.
3. 下列各式计算正确的是(    )
A. 2a2+3a2=5a4 B. (−2ab)3=−6ab3
C. (3a+b)(3a−b)=9a2−b2 D. a3⋅(−2a)=−2a3
4. “柳条初弄绿，已觉春风驻”.每到春天，人们在欣赏柳绿桃红的同时，也被飞舞的柳絮所烦恼，据了解柳絮纤维的直径约为0.00105cm，则0.00105用科学记数法可表示为(    )
A. −1.05×103 B. 1.05×10−3 C. 1.05×10−4 D. 105×10−5
5. 如图，由几个相同的小正方体搭成一个几何体，从上面观察该图形，得到的平面图形是(    )
A.
B.
C.
D.
6. 甲、乙、丙、丁四人各进行了6次跳远测试，他们的平均成绩相同，方差分别是S甲2=0.65，S乙2=0.55，S丙2=0.50，S丁2=0.45，则跳远成绩最稳定的是(    )
A. 甲 B. 乙 C. 丙 D. 丁
7. “劳动创造世界”，劳动教育已纳入国家人才培养全过程．某学农基地加大投入，建设新型农场，该农场一种作物的亩产量两年内从400千克增加到484千克．设平均每年增产的百分率为x，则可列方程为(    )
A. 400(1+2x)=484 B. 400(1+x)2=484
C. 400(1+x)=484 D. 400(1+x2)=484
8. 一天早上，小万沿花园匀速按顺时针方向散步，已知小万从花园的点A处开始散步，将小万看作动点B，花园的中心为O.设在散步过程中，小万，点O，点A所形成的夹角(∠AOB)的度数为y°(此处y≤180)，y随时间x变化的图象如图，则花园的形状可能是(    )
A. B. C. D.

二、填空题（本大题共8小题，共24分）
9. 若代数式xx−2有意义，则实数x的取值范围是______．
10. 分解因式：x2−4y2=______．
11. 关于x的一元二次方程kx2+2x−1=0没有实数根，则k的取值范围是______．
12. 如图，在已知的△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于12BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠A=50°，则∠ACB=______．

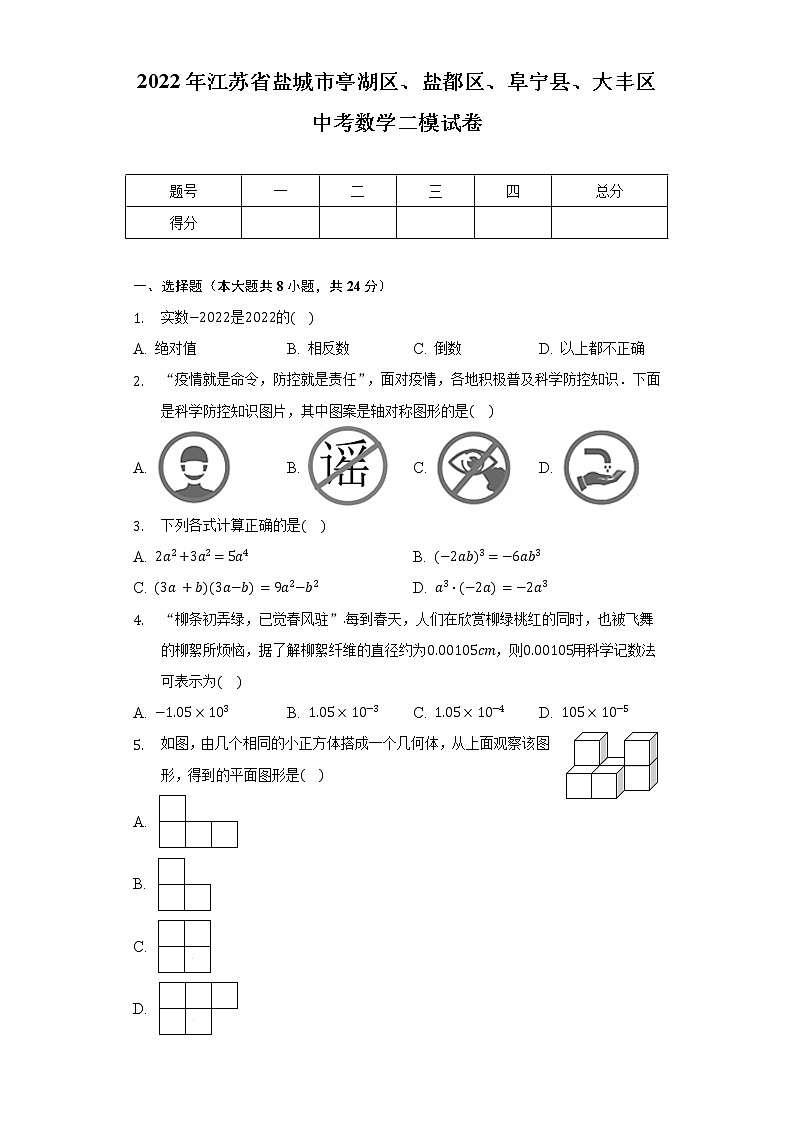
13. 一个不透明的袋子里装有黑白两种颜色的球共40个，这些球除颜色外都相同．小贤从袋子中随机摸一个球，记下颜色后放回，不断重复，并绘制了如图所示的统计图，则这个袋中黑球的个数最有可能是______．

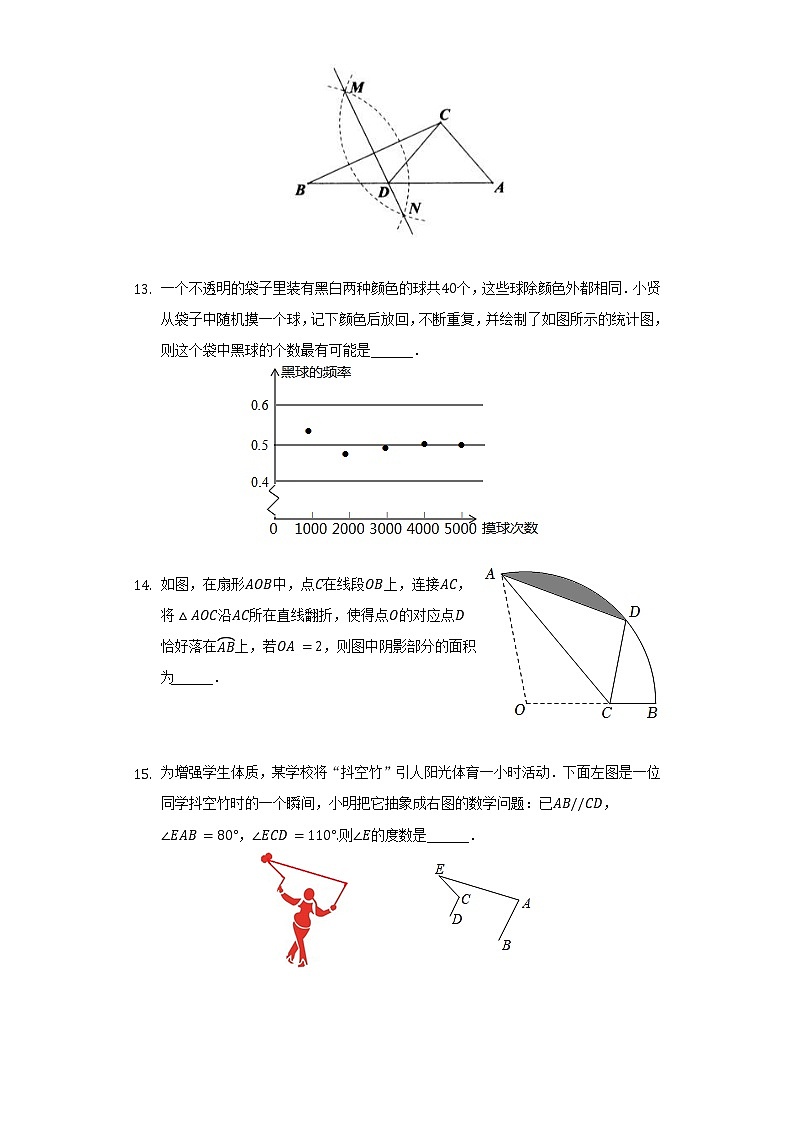
14. 如图，在扇形AOB中，点C在线段OB上，连接AC，将△AOC沿AC所在直线翻折，使得点O的对应点D恰好落在AB上，若OA=2，则图中阴影部分的面积为______．



15. 为增强学生体质，某学校将“抖空竹”引人阳光体育一小时活动．下面左图是一位同学抖空竹时的一个瞬间，小明把它抽象成右图的数学问题：已AB//CD，∠EAB=80°，∠ECD=110°.则∠E的度数是______．

16. 如图，在矩形ABCD中，AB=8，AD=6，点P为矩形ABCD内一点，满足∠APB=90°，连接C、P两点，并延长CP交直线AB于点E.若点P是线段CE的中点，则BE=______．

三、计算题（本大题共1小题，共6分）
17. 计算：38+|−6|−22．

四、解答题（本大题共10小题，共96分）
18. 化简(1−1x−1)÷x2−4x+4x2−1．
19. 如图，AD是△ABC的中线，tanB=13，cosC=22，AC=2.求：
(1)BC的长；
(2)sin∠ADC的值．
20. 小红的爸爸积极参加社区抗疫志愿服务工作．根据社区的安排，志愿者被随机分到A组(体温检测)、B组(便民代购)、C组(环境消杀)．
(1)小红的爸爸被分到B组的概率是______；
(2)某中学王老师也参加了该社区的志愿者队伍，他和小红爸爸被分到同一组的概率是多少？(请用画树状图或列表的方法写出分析过程)
21. 已知A(−4,m+10)、B(n,−4)两点是一次函数y=kx+b和反比例函数y=mx图象的交点．
(1)求一次函数和反比例函数的解析式；
(2)连接OA、OB，求△AOB的面积．

22. 如图，在平行四边形ABCD中，点O是BC的中点，连接DO并延长，交AB延长线于点E，连接BD，EC．

(1)求证：四边形BECD是平行四边形；
(2)若∠A=50°，则当∠ADE=______°时，四边形BECD是菱形．
23. 甲、乙、丙三个家电厂家在广告中都声称，他们的某种电子产品在正常情况下的使用寿命都是8年，经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查，统计结果如下：(单位：年)
甲厂：4，5，5，5，5，7，9，12，13，15
乙厂：6，6，8，8，8，9，10，12，14，15
丙厂：4，4，4，6，7，9，13，15，16，16
请回答下面问题：
(1)填空：

平均数
众数
中位数
甲厂
______
______
6
乙厂
9.6
______
8.5
丙厂
9.4
4
______
(2)这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数？
(3)你是顾客，你买三家中哪一家的电子产品？为什么？
24. 某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种玩具．据了解，8只“冰墩墩”和10只“雪容融”的进价共计2000元；10只“冰墩墩”和20只“雪容融”的进价共计3100元．
(1)求“冰墩墩”和“雪容融”两种玩具每只进价分别是多少元；
(2)若“冰墩墩”和“雪容融”两种玩具每只售价分别是200元、100元．该专卖店计划恰好用3500元购进“冰墩墩”和“雪容融”两种玩具(两种均买)，请帮助专卖店设计采购方案，使得总利润最大．
25. 如图，AB是⊙O的直径，点C在⊙O上，∠ABC的平分线与AC相交于点D，与⊙O过点A的切线相交于点E．
(1)∠ACB=______°，理由是：______；
(2)猜想△EAD的形状，并证明你的猜想；
(3)若AB=8，AD=6，求BD．



26. 若二次函数y=ax2+bx+a+2的图象经过点A(1,0)，其中a、b为常数．
(1)用含有字母a的代数式表示抛物线顶点的横坐标；
(2)点B(−12,1)、C(2,1)为坐标平面内的两点，连接B、C两点．
①若抛物线的顶点在线段BC上，求a的值；
②若抛物线与线段BC有且只有一个公共点，求a的取值范围．

27. 以下为一个合作学习小组在一次数学研讨中的过程记录，请阅读后完成下方的问题1～4．
试题分析
(Ⅰ)如图1，在Rt△ABC中，∠BAC=90°，AB=AC，D是△ABC外一点，且AD=AC.求∠BDC的度数．
小明：我发现试题中有三个等腰三角形，设∠ADB=α，易知∠CAD=90°−2α，又因为AD=AC，得∠ADC=45°+α，即可算出∠BDC的度数．
小丽：我发现AB=AC=AD.则点B、C、D到点A的距离相等，所以点B、C、D在以点A为圆心、线段AB长为半径的圆上……
猜想证明
(Ⅱ)如图1，在Rt△ABC中，∠BAC=90°，AB=AC，点D、A在BC同侧．
猜想：若∠BDC=______°，则点D在以点A为圆心、线段AB长为半径的圆上．
对于这个猜想的证明，小华有自己的想法：
以点A为圆心，AB长为半径画圆．根据点与圆的位置关系，知道点D可能在⊙A内，或点D在⊙A上，或点D在⊙A外．故只要证明点D不在⊙A内，也不在⊙A外，就可以确定点D一定在⊙A上．
(Ⅲ)进一步猜想：
如图2，在△ABC中，∠BAC=β，AB=AC，点D、A在BC同侧．若∠BDC=______°，则点D在以点A为圆心、线段AB长为半径的圆上．
(Ⅳ)对(Ⅲ)中的猜想进行证明．
问题1.完成(Ⅰ)中的求解过程；
问题2.补全猜想证明中的两个猜想：(Ⅱ) ______；(Ⅲ) ______；
问题3.证明上面(Ⅲ)中的猜想；
问题4.如图3为某大型舞台实景投影侧面示意图，∠BOC=90°，点A处为投影机，投影角∠BAC=45°，折线B−O−C为影像接收区．若影像接收区最大时(即OB+OC最大)，投射效果最好，请直接写出影像接收区最大时OB的长______．
答案和解析

1.【答案】B
【解析】解：−2022和2022互为相反数，
故选：B．
根据绝对值，相反数，倒数的定义判断即可．
本题考查了实数的性质，绝对值，相反数，倒数，掌握只有符号不同的两个数互为相反数是解题的关键．

2.【答案】A
【解析】解：选项A能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是做轴对称图形；
选项B、C、D均不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是做轴对称图形；
故选：A．
结合轴对称图形的概念进行求解即可．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．
本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．

3.【答案】C
【解析】
【分析】
此题考查了平方差公式，合并同类项，幂的乘方与积的乘方，以及单项式乘以单项式，熟练掌握 公式及法则是解本题的关键．
各项利用合并同类项法则，幂的乘方与积的乘方，平方差公式，以及单项式乘以单项式法则判断即可．
【解答】
解： A 、原式 =5a2 ，不符合题意；
B 、原式 =−8a3b3 ，不符合题意；
C 、原式 =9a2−b2 ，符合题意；
D 、原式 =−2a4 ，不符合题意，
故选 C ．   
4.【答案】B
【解析】解：0.00105=1.05×10−3．
故选：B．
绝对值小于1的负数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数n由原数左边起第一个不为零的数字前面的0的个数所决定．
此题主要考查了用科学记数法表示较小的数，一般形式为a×10−n，其中1≤|a|