2020-2021学年广东省广州市白云区、海珠区高一（下）期末数学试卷

这是一份2020-2021学年广东省广州市白云区、海珠区高一（下）期末数学试卷，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
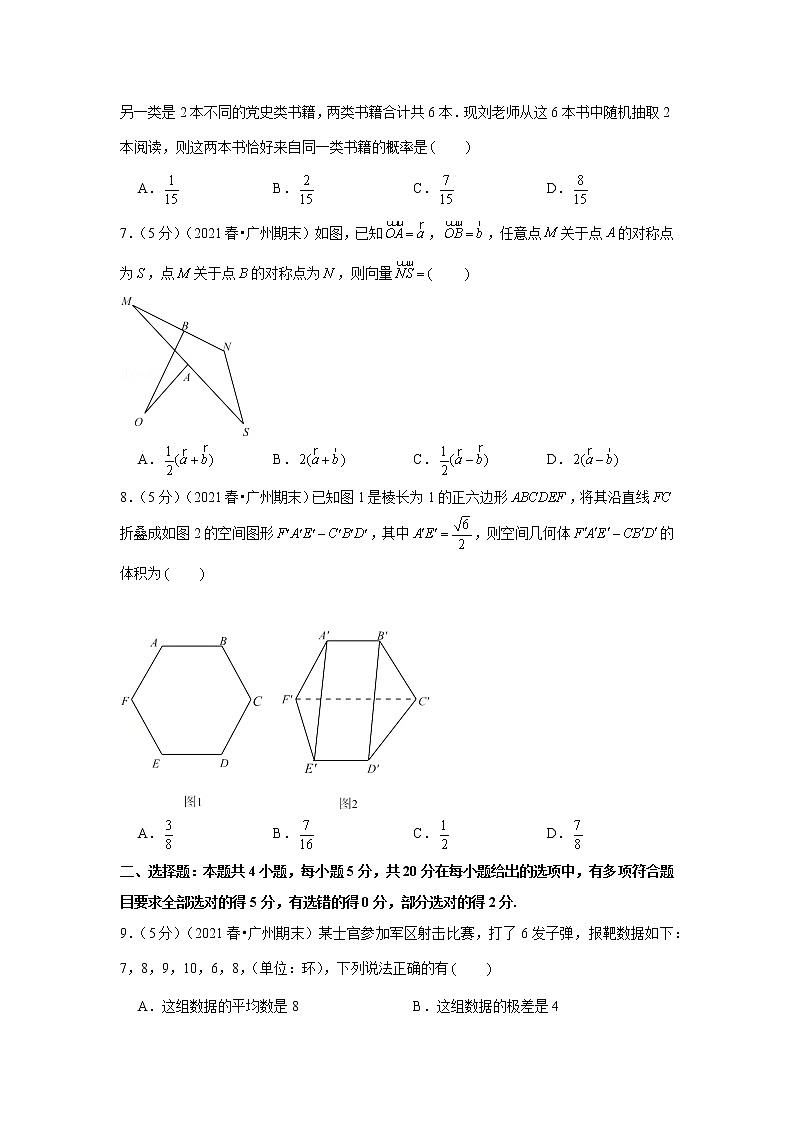
2020-2021学年广东省广州市白云区、海珠区高一（下）期末数学试卷一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）（2021春•广州期末）若复数为虚数单位），则　　A． B．1 C．5 D．2．（5分）（2021春•广州期末）已知向量，，且，则　　A． B．9 C． D．43．（5分）（2021春•广州期末）高一年级有男生510人，女生490人，小明按男女比例进行分层随机抽样，总样本量为100．则在男生中抽取的样本量为　　A．48 B．51 C．50 D．494．（5分）（2021春•广州期末）如图，△是水平放置的的斜二测直观图，△为等腰直角三角形，其中与重合，，则的面积是　　A．9 B． C．18 D．5．（5分）（2021春•广州期末）已知，，与的夹角为，则　　A． B．72 C．84 D．6．（5分）（2021春•广州期末）某学校开展“学党史，颂党恩，跟党走“学习活动，刘老师去购书中心购买了一批书籍作为阅读学习之用，其中一类是4本不同的红色经典小说类书籍，另一类是2本不同的党史类书籍，两类书籍合计共6本．现刘老师从这6本书中随机抽取2本阅读，则这两本书恰好来自同一类书籍的概率是　　A． B． C． D．7．（5分）（2021春•广州期末）如图，已知，，任意点关于点的对称点为，点关于点的对称点为，则向量　　A． B． C． D．8．（5分）（2021春•广州期末）已知图1是棱长为1的正六边形，将其沿直线折叠成如图2的空间图形，其中，则空间几何体的体积为　　 A． B． C． D．二、选择题：本题共4小题，每小题5分，共20分在每小题给出的选项中，有多项符合题目要求全部选对的得5分，有选错的得0分，部分选对的得2分.9．（5分）（2021春•广州期末）某士官参加军区射击比赛，打了6发子弹，报靶数据如下：7，8，9，10，6，8，（单位：环），下列说法正确的有　　A．这组数据的平均数是8 B．这组数据的极差是4 C．这组数据的中位数是8.5 D．这组数据的方差是210．（5分）（2021春•广州期末）已知复数为虚数单位），下列说法正确的有　　A．当时，复平面内表示复数的点位于第二象限 B．当时，为纯虚数 C．最大值为 D．的共轭复数为11．（5分）（2021春•广州期末）某班级到一工厂参加社会实践劳动，加工出如图所示的圆台，在轴截面中，，且，下列说法正确的有　　A．该圆台轴截面面积为 B．该圆台的体积为 C．该圆台的母线与下底面所成的角为 D．沿着该圆台表面，从点到中点的最短距离为12．（5分）（2021春•广州期末）在中，角，，所对的边分别为，，，点为所在平面内点，满足，下列说法正确的有　　A．若，则点为的重心 B．若，则点为的外心 C．若，，，则点为的内心 D．若，，，则点为的垂心三、填空题：本题共4小题，每小题5分，共20分.13．（5分）（2021春•广州期末）有10种不同的零食，每100克可食部分包含的能量（单位：如下：100，120，125，165，430，190，175，234，425，310这10种零食每100克可食部分的能量的第60百分位数为 　　．14．（5分）（2021春•广州期末）天气预报元旦假期甲地的降雨概率是0.2，乙地的降雨概率是0.3，假定在这段时间内两地是否降雨相互之间没有影响，则在这段时间内甲，乙两地只有一个地方降雨的概率是 　　．15．（5分）（2021春•广州期末）如图，在三棱锥中，，，则二面角的余弦值为 　　．16．（5分）（2021春•广州期末）如图，是边长为1的正三角形，，分别为线段，上一点，满足，，与的交点为，则线段的长度为 　　．四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.17．（10分）（2021春•广州期末）现有两个红球（记为，，两个白球（记为，，采用不放回简单随机抽样从中任意抽取两球．（1）写出试验的样本空间；（2）求恰好抽到一个红球一个白球的概率．18．（12分）（2021春•广州期末）已知角是的内角，若，，．（1）若，求角的值；（2）设，当取最大值时，求在上的投影向量（用坐标表示）．19．（12分）（2021春•广州期末）如图，直三棱柱中，是的中点．（1）求证：直线平面；（2）若，求异面直线与所成角的大小．20．（12分）（2021春•广州期末）2021年五一假期，各高速公路车流量大，交管部门在某高速公路区间测速路段随机抽取40辆汽车进行车速调查，将这40辆汽车在该区间测速路段的平均车速分成六段，，，，，，，，，，，，得到如图的频率分布直方图．（1）根据频率分布直方图估计出这40辆汽车的平均车速的中位数；（2）现从平均车速在区间，的车辆中任意抽取2辆汽车，求抽取的2辆汽车的平均车速都在区间，上的概率；（3）出于安全考虑，测速系统对平均车速在区间，的汽车以实时短信形式对车主进行安全提醒，确保行车安全．假设每辆在此区间测速路段行驶的汽车平均车速相互不受影响，以此次调查的样本频率估计总体概率，求连续2辆汽车都收到短信提醒的概率？21．（12分）（2021春•广州期末）如图，垂直于所在的平面，为的直径，，，，，点为线段上一动点．（1）证明：平面平面；（2）当点移动到点时，求与平面所成角的正弦值．22．（12分）（2021秋•阳江期末）为响应国家“乡村振兴”号召，农民王大伯拟将自家一块直角三角形地按如图规划成3个功能区：区域为荔枝林和放养走地鸡，区域规划为“民宿”供游客住宿及餐饮，区域规划为小型鱼塘养鱼供休闲垂钓．为安全起见，在鱼塘周围筑起护栏．已知，，，（1）若时，求护栏的长度的周长）；（2）若鱼塘的面积是“民宿” 的面积的倍，求；（3）当为何值时，鱼塘的面积最小，最小面积是多少？
2020-2021学年广东省广州市白云区、海珠区高一（下）期末数学试卷参考答案与试题解析一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）（2021春•广州期末）若复数为虚数单位），则　　A． B．1 C．5 D．【解答】解：，，故选：．2．（5分）（2021春•广州期末）已知向量，，且，则　　A． B．9 C． D．4【解答】解：，，解得．故选：．3．（5分）（2021春•广州期末）高一年级有男生510人，女生490人，小明按男女比例进行分层随机抽样，总样本量为100．则在男生中抽取的样本量为　　A．48 B．51 C．50 D．49【解答】解：高一年级共有人，所以男生抽取的人数为人．故选：．4．（5分）（2021春•广州期末）如图，△是水平放置的的斜二测直观图，△为等腰直角三角形，其中与重合，，则的面积是　　A．9 B． C．18 D．【解答】解：在斜二测直观图中，由△为等腰直角三角形，，可得，还原原图形如图：则，，则．故选：．5．（5分）（2021春•广州期末）已知，，与的夹角为，则　　A． B．72 C．84 D．【解答】解：，，与的夹角为，，则．故选：．6．（5分）（2021春•广州期末）某学校开展“学党史，颂党恩，跟党走“学习活动，刘老师去购书中心购买了一批书籍作为阅读学习之用，其中一类是4本不同的红色经典小说类书籍，另一类是2本不同的党史类书籍，两类书籍合计共6本．现刘老师从这6本书中随机抽取2本阅读，则这两本书恰好来自同一类书籍的概率是　　A． B． C． D．【解答】解：从6本书中随机抽取2本，共有种取法，若两本书来自同一类书籍则有种取法，所以两本书恰好来自同一类书籍的概率是．故选：．7．（5分）（2021春•广州期末）如图，已知，，任意点关于点的对称点为，点关于点的对称点为，则向量　　A． B． C． D．【解答】解：，，任意点关于点的对称点为，点关于点的对称点为，是的中位线，．故选：．8．（5分）（2021春•广州期末）已知图1是棱长为1的正六边形，将其沿直线折叠成如图2的空间图形，其中，则空间几何体的体积为　　 A． B． C． D．【解答】解：如图， 过作，垂足为，连接，则，过作，垂足为，连接，则，可得平面平面，即三棱柱为直三棱柱．，，可得，，同理求得，，又，，空间几何体的体积为．故选：．二、选择题：本题共4小题，每小题5分，共20分在每小题给出的选项中，有多项符合题目要求全部选对的得5分，有选错的得0分，部分选对的得2分.9．（5分）（2021春•广州期末）某士官参加军区射击比赛，打了6发子弹，报靶数据如下：7，8，9，10，6，8，（单位：环），下列说法正确的有　　A．这组数据的平均数是8 B．这组数据的极差是4 C．这组数据的中位数是8.5 D．这组数据的方差是2【解答】解：对于，这组数据的平均数是，故正确；对于，这组数据的极差是，故正确；对于，这组数据从小到大为6，7，8，8，9，10，这组数据的中位数是8，故错误；对于，这组数据的方差是，故错误．故选：．10．（5分）（2021春•广州期末）已知复数为虚数单位），下列说法正确的有　　A．当时，复平面内表示复数的点位于第二象限 B．当时，为纯虚数 C．最大值为 D．的共轭复数为【解答】解：对于，当时，，复平面内表示复数的点位于第四象限，故错误；对于，当时，，为纯虚数，故正确；对于，，最大值为，故正确；对于，的共轭复数为，故错误．故选：．11．（5分）（2021春•广州期末）某班级到一工厂参加社会实践劳动，加工出如图所示的圆台，在轴截面中，，且，下列说法正确的有　　A．该圆台轴截面面积为 B．该圆台的体积为 C．该圆台的母线与下底面所成的角为 D．沿着该圆台表面，从点到中点的最短距离为【解答】解：由，且，可得，高，则圆台轴截面面积为，故正确；圆台的体积为，故正确；圆台的母线与下底面所成的角为，其正弦值为，所以，故错误；由圆台补成圆锥，可得大圆锥的母线长为，底面半径为，侧面展开图的圆心角为，设的中点为，连接，可得，，，则，所以沿着该圆台表面，从点到中点的最短距离为，故正确．故选：．12．（5分）（2021春•广州期末）在中，角，，所对的边分别为，，，点为所在平面内点，满足，下列说法正确的有　　A．若，则点为的重心 B．若，则点为的外心 C．若，，，则点为的内心 D．若，，，则点为的垂心【解答】解：若则，．取中点，连接， ．在的中线上，同理可得在其它两边的中线上，是的重心．若，，，则有，延长交于，则，， ，设，则，与共线，与，不共线，，，，为的平分线，同理可证其它的两条也是角平分线．是的内心．故选：．三、填空题：本题共4小题，每小题5分，共20分.13．（5分）（2021春•广州期末）有10种不同的零食，每100克可食部分包含的能量（单位：如下：100，120，125，165，430，190，175，234，425，310这10种零食每100克可食部分的能量的第60百分位数为 　212　．【解答】解：根据题意，将10个数据从小到大排列：100，120，125，165，175，190，234，310，425，430；，则该组数据的第60百分位数为，故答案为：212．14．（5分）（2021春•广州期末）天气预报元旦假期甲地的降雨概率是0.2，乙地的降雨概率是0.3，假定在这段时间内两地是否降雨相互之间没有影响，则在这段时间内甲，乙两地只有一个地方降雨的概率是 　0.38　．【解答】解：根据题意，设事件表示甲地下雨，事件表示乙地下雨，（A），（B），甲，乙两地只有一个地方降雨的概率；故答案为：0.38．15．（5分）（2021春•广州期末）如图，在三棱锥中，，，则二面角的余弦值为 　　．【解答】解：取的中点，连接、，因为，所以，，所以即为二面角的平面角，因为，，所以，而，在中，由余弦定理可得，故答案为：．16．（5分）（2021春•广州期末）如图，是边长为1的正三角形，，分别为线段，上一点，满足，，与的交点为，则线段的长度为 　　．【解答】解：以为原点，为轴，建立如图所示的平面直角坐标系，则，，，，，，，，所以直线的方程为，即，直线的方程为，即，联立，解得，即，，所以．故答案为：．四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.17．（10分）（2021春•广州期末）现有两个红球（记为，，两个白球（记为，，采用不放回简单随机抽样从中任意抽取两球．（1）写出试验的样本空间；（2）求恰好抽到一个红球一个白球的概率．【解答】解：（1）两个红球（记为，，两个白球（记为，，采用不放回简单随机抽样从中任意抽取两球，则试验的样本空间，，，，，，，，，，，．（2）试验的样本空间，，，，，，，，，，，，包含6个样本点，其中恰好抽到一个红球一个白球包含4个样本点，恰好抽到一个红球一个白球的概率．18．（12分）（2021春•广州期末）已知角是的内角，若，，．（1）若，求角的值；（2）设，当取最大值时，求在上的投影向量（用坐标表示）．【解答】解：（1）角是的内角，，又，，且，，即，，，，则，即；（2），，要使取得最大值，则，即．，，，在上的投影向量为，，．19．（12分）（2021春•广州期末）如图，直三棱柱中，是的中点．（1）求证：直线平面；（2）若，求异面直线与所成角的大小．【解答】解：（1）证明：连接，交于点，连接，直三棱柱中，是矩形，是中点，是的中点，，平面，平面，直线平面；（2）解法一：，是的中点，，直三棱柱中，平面，平面，，，平面，平面，，异面直线与所成角的大小为．解法二：，是的中点，，以为原点，为轴，为轴，过作平面的垂线为轴，建立空间直角坐标系，设，，，则，0，，，0，，，，，，0，，，0，，，，，，，异面直线与所成角的大小为．20．（12分）（2021春•广州期末）2021年五一假期，各高速公路车流量大，交管部门在某高速公路区间测速路段随机抽取40辆汽车进行车速调查，将这40辆汽车在该区间测速路段的平均车速分成六段，，，，，，，，，，，，得到如图的频率分布直方图．（1）根据频率分布直方图估计出这40辆汽车的平均车速的中位数；（2）现从平均车速在区间，的车辆中任意抽取2辆汽车，求抽取的2辆汽车的平均车速都在区间，上的概率；（3）出于安全考虑，测速系统对平均车速在区间，的汽车以实时短信形式对车主进行安全提醒，确保行车安全．假设每辆在此区间测速路段行驶的汽车平均车速相互不受影响，以此次调查的样本频率估计总体概率，求连续2辆汽车都收到短信提醒的概率？【解答】解：（1）设平均车速的中位数的估值为，则故平均车速的中位数为107.5．（2）车速在，内的有，车速在，的有，故抽取的2辆汽车的平均车速都在区间，上的概率．（3）设事件为“汽车收到短信提醒”，则，汽车的速度不受影响，连续两辆汽车都收到短信体现的概率．21．（12分）（2021春•广州期末）如图，垂直于所在的平面，为的直径，，，，，点为线段上一动点．（1）证明：平面平面；（2）当点移动到点时，求与平面所成角的正弦值．【解答】（1）证明：因为垂直于所在的平面，即平面，平面，所以，又为的直径，所以，因为，所以平面，又平面，所以，因为，，所以平面，又平面，所以平面平面．（2）解：因为，，所以，又，所以，由，可得，如图，过点作交于点，则，可得，又，所以，所以，，设点到平面的距离为，由，可得，解得，所以当点移动到点时，与平面所成角的正弦值为．22．（12分）（2021秋•阳江期末）为响应国家“乡村振兴”号召，农民王大伯拟将自家一块直角三角形地按如图规划成3个功能区：区域为荔枝林和放养走地鸡，区域规划为“民宿”供游客住宿及餐饮，区域规划为小型鱼塘养鱼供休闲垂钓．为安全起见，在鱼塘周围筑起护栏．已知，，，（1）若时，求护栏的长度的周长）；（2）若鱼塘的面积是“民宿” 的面积的倍，求；（3）当为何值时，鱼塘的面积最小，最小面积是多少？【解答】解：（1），，，，，，，在中，由余弦定理可得，则，，，，，，护栏的长度的周长）为；（2）设，因为鱼塘的面积是“民宿” 的面积的倍，所以，即，在中，由，得，从而，即，由，得，所以，即，（3）设，由（2）知，又在中，由，得，所以，所以当且仅当，即时，的面积取最小值为．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/6/13 19:28:26；用户：13159259195；邮箱：13159259195；学号：39016604