

湖北省黄冈市2020-2021学年高一下学期期末考试调研考试数学试卷及参考答案
展开2020-2021学年湖北省黄冈市高一(下)期末数学试卷
一、单项选择题(共8小题,每小题5分,共40分).
1.已知i为虚数单位,复数z满足z(3+i)=2﹣i,则下列说法正确的是( )
A.复数z的模为
B.复数z的共轭复数为
C.复数z的虚部为
D.复数z在复平面内对应的点在第二象限
2.在△ABC中,a=15,b=10,A=45°,则cosB=( )
A. B.﹣ C. D.﹣
3.不同的直线m和n,不同的平面α,β,γ,下列条件中能推出α∥β的是( )
A.α∩γ=n,β∩γ=m,n∥m B.α⊥γ,β⊥γ
C.n∥m,n⊥α,m⊥β D.n∥α,m∥β,n∥m
4.若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积是球体积两倍时,该圆锥的高为( )
A.2 B.4 C. D.
5.一个正方体有一个面为红色,两个面为绿色,三个面为黄色,另一个正方体有两个面为红色,两个面为绿色,两个面为黄色,同时掷这两个正方体,两个正方体朝上的面颜色不同的概率为( )
A. B. C. D.
6.如图,正三棱锥A﹣BCD中,∠BAD=20°,侧棱长为2,过点C的平面与侧棱AB、AD相交于B1、D1,则△CB1D1的周长的最小值为( )
A. B. C.4 D.2
7.如图所示,△ABC中,AB=3,AC=2,∠BAC=60°,D是BC的中点,,则=( )
A. B. C. D.
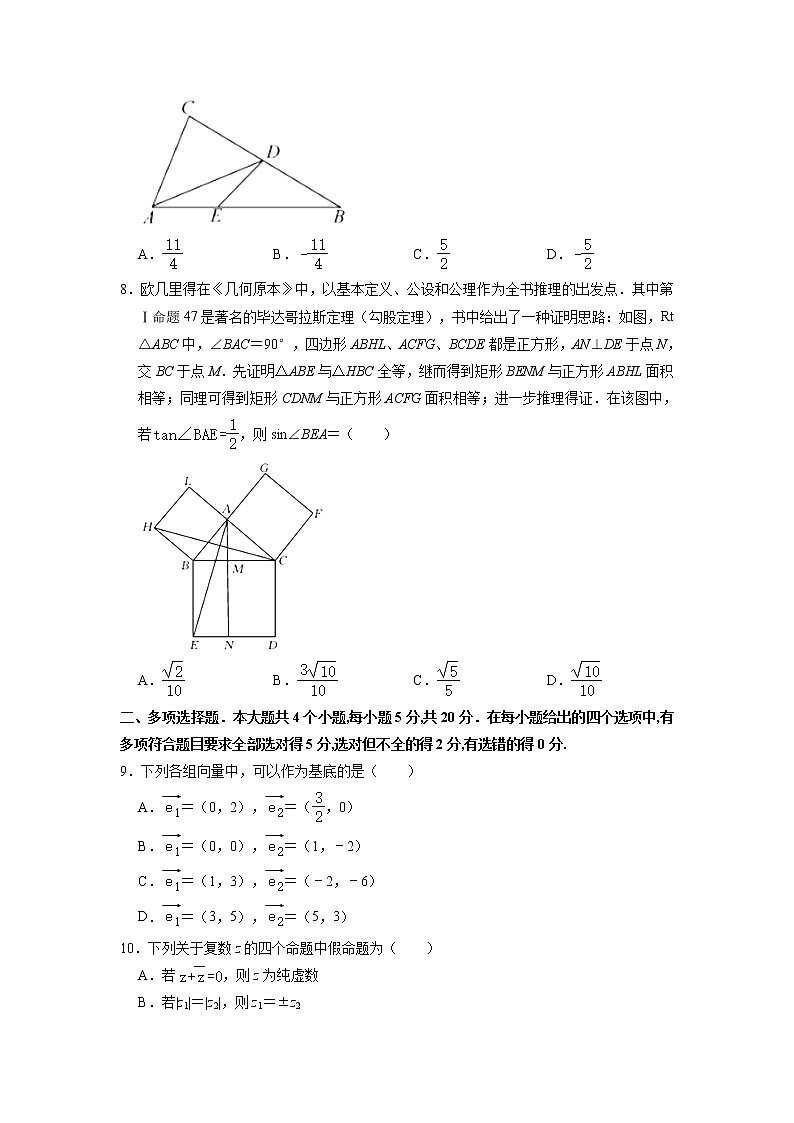
8.欧几里得在《几何原本》中,以基本定义、公设和公理作为全书推理的出发点.其中第Ⅰ命题47是著名的毕达哥拉斯定理(勾股定理),书中给出了一种证明思路:如图,Rt△ABC中,∠BAC=90°,四边形ABHL、ACFG、BCDE都是正方形,AN⊥DE于点N,交BC于点M.先证明△ABE与△HBC全等,继而得到矩形BENM与正方形ABHL面积相等;同理可得到矩形CDNM与正方形ACFG面积相等;进一步推理得证.在该图中,若,则sin∠BEA=( )
A. B. C. D.
二、多项选择题.本大题共4个小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求全部选对得5分,选对但不全的得2分,有选错的得0分.
9.下列各组向量中,可以作为基底的是( )
A.=(0,2),=(,0)
B.=(0,0),=(1,﹣2)
C.=(1,3),=(﹣2,﹣6)
D.=(3,5),=(5,3)
10.下列关于复数z的四个命题中假命题为( )
A.若,则z为纯虚数
B.若|z1|=|z2|,则z1=±z2
C.若|z﹣i|=1,则|z|的最大值为2
D.若z3﹣1=0,则z=1
11.如图在三棱柱ABC﹣A1B1C1中,CC1⊥底面ABC,AC⊥CB,点D是AB上的动点,则下列结论正确的是( )
A.BC⊥AC1
B.当D为AB的中点时,平面CDB1⊥平面AA1B1B
C.当D为AB中点时,AC1∥平面CDB1
D.三棱锥A1﹣CDB1的体积是定值
12.在△ABC中,内角A,B,C所对的边分别为a,b,c,则下列说法中正确的是( )
A.c=acosB+bcosA
B.若acosA=bcosB,则△ABC为等腰三角形
C.若a2tanB=b2tanA,则a=b
D.若a3+b3=c3,则△ABC为锐角三角形
三、填空题(本题共4个小题,每题5分,共20分)
13.一个口袋中装有2个红球,3个绿球,采用不放回的方式从中依次取出2个球,则第一次取到绿球第二次取到红球的概率为 .
14.在△ABC中,D是BC的中点,AB=1,AC=2,AD=,则△ABC的面积为 .
15.如图,正方体ABCD﹣A1B1C1D1中,O是AC的中点,直线B1O与平面ACD1所成角的正弦值为 .
16.如图等腰梯形ABCD中,AB∥CD,,O是梯形ABCD的外接圆的圆心,M是边BC上的中点,则的值为 .
三、解答题:本大题共6个小题,共70分,解答应写出文字说明,证明过程或验算步骤.
17.复数z满足|z|=,z2为纯虚数,若复数z在复平面内所对应的点在第一象限.
(1)求复数z;
(2)复数z,,z2所对应的向量为,,,已知(λ+)⊥(λ+),求λ的值.
18.△ABC的内角A,B,C的对边分别为a,b,c,已知,
(1)求角A;
(2)若a=,△ABC的面积为,求△ABC的周长.
19.黄冈市一中学高一年级统计学生本学期20次数学周测成绩(满分150),抽取了甲乙两位同学的20次成绩记录如下:
甲:92,96,99,103,104,105,113,114,117,117,121,123,124,126,129,132,134,136,142,141
乙:102,105,113,114,116,117,125,125,127,128,128,131,131,135,136,138,139,142,145,150
(1)根据以上记录数据求甲乙两位同学成绩的中位数,并据此判断甲乙两位同学的成绩谁更好?
(2)将同学乙的成绩分成[100,110),[120,130)[130,140)[140,150),完成下列频率分布表,并画出频率分布直方图;
(3)现从甲乙两位同学的不低于140分的成绩中任意取出2个成绩,求取出的2个成绩不是同一个人的且没有满分的概率.
分组
频数
频率
[100,110)
[110,120)
[120,130)
[130,140)
[140,150]
合计
20
1
20.如图,已知在四棱锥P﹣ABCD中,底面ABCD是梯形,BC∥AD且BC=2AD,平面PAC⊥平面ABCD,PA=PC,PA⊥AB.
(1)证明:AB⊥PC;
(2)若PA⊥PC,PB=2PC=4,求四棱锥P﹣ABCD的体积.
21.如图,四边形ABCD中,∠BAC=90°,∠ABC=60°,AD⊥CD,设∠ACD=θ.
(1)若△ABC面积是△ACD面积的4倍,求sin2θ;
(2)若tan∠ADB=,求tanθ.
22.如图①梯形ABCD中AD∥BC,AB=,BC=1,,BE⊥AD且BE=1,将梯形沿BE折叠得到图②,使平面ABE⊥平面BCDE,CE与BD相交于O,点P在AB上,且AP=2PB,R是CD的中点,过O,P,R三点的平面交AC于Q.
(1)证明:Q是的中点;
(2)证明:AD⊥平面BEQ;
(3)M是AB上一点,已知二面角M﹣EC﹣B为45°,求的值.
参考答案
一、单项选择题(共8小题,每小题5分,共40分).
1.已知i为虚数单位,复数z满足z(3+i)=2﹣i,则下列说法正确的是( )
A.复数z的模为
B.复数z的共轭复数为
C.复数z的虚部为
D.复数z在复平面内对应的点在第二象限
【分析】直接利用复数的运算,复数的共轭运算,复数的模,复数表示的几何意义的应用判断A、B、C、D的结论.
解:复数z满足z(3+i)=2﹣i,整理得:,
对于A:,故A正确;
对于B:复数z的共轭复数为,故B错误;
对于C:复数z的虚部为,故C错误;
对于D:复数z在复平面内对应的点在第四象限,故D错误.
故选:A.
2.在△ABC中,a=15,b=10,A=45°,则cosB=( )
A. B.﹣ C. D.﹣
【分析】根据正弦定理可得:sinB==,由a=15>b=10,由大边对大角可得:0<B<A=45°,故可求cosB的值.
解:根据正弦定理可得:sinB===,
∵a=15>b=10,
∴由大边对大角可得:0<B<A=45°,
∴cosB==.
故选:C.
3.不同的直线m和n,不同的平面α,β,γ,下列条件中能推出α∥β的是( )
A.α∩γ=n,β∩γ=m,n∥m B.α⊥γ,β⊥γ
C.n∥m,n⊥α,m⊥β D.n∥α,m∥β,n∥m
【分析】利用平面平行的判定定理,对四个选项分别进行判断,能够得到正确答案.
解:由不同的直线m和n,不同的平面α,β,γ,知:
若α∩γ=n,β∩γ=m,n∥m,则α与β相交或平行,故A不正确;
若α⊥γ,β⊥γ,则α与β相交或平行,故B不正确;
若n∥m,n⊥α,m⊥β,则由平面平行的判定定理知α∥β,故C正确;
若n∥α,m∥β,n∥m,则α与β相交或平行,故D不正确.
故选:C.
4.若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积是球体积两倍时,该圆锥的高为( )
A.2 B.4 C. D.
【分析】利用体积公式求出圆锥底面圆半径r与高h的关系,再通过球与圆锥相切,利用等面积法列出r与h的另一组关系,通过解方程组求解.
解:如图,圆锥的轴截面为等腰△SAB,且内切圆为球的大圆.设圆锥底面圆周的半径为r,高为h,球的半径为R,R=1.
则由条件有,整理得r2h=8①
在△SAB中,,所以②,
联立①②,解得.
故选:B.
5.一个正方体有一个面为红色,两个面为绿色,三个面为黄色,另一个正方体有两个面为红色,两个面为绿色,两个面为黄色,同时掷这两个正方体,两个正方体朝上的面颜色不同的概率为( )
A. B. C. D.
【分析】根据已知条件,结合古典概型的概率公式,可得两个正方体朝上的面颜色相同的概率,再求其对立事件的概率,即可求解.
解:第一个正方体出现红色,绿色,黄色的概率分别为,第二个正方体出现红色,绿色,黄色的概率分别为,
∵两个正方体朝上的面颜色相同的概率为,
∴两个正方体朝上的面颜色不同的概率为1﹣=.
故选:C.
6.如图,正三棱锥A﹣BCD中,∠BAD=20°,侧棱长为2,过点C的平面与侧棱AB、AD相交于B1、D1,则△CB1D1的周长的最小值为( )
A. B. C.4 D.2
【分析】首先,展开三棱锥,然后,两点间的连接线CC'即是截面周长的最小值,然后,求解其距离即可.
解:把正三棱锥A﹣BCD的侧面展开,
两点间的连接线CC'即是截面周长的最小值.
正三棱锥A﹣BCD中,∠BAD=20°,所以,∠CAC′=60°,AC=2,
∴CC′=2,
∴截面周长最小值是CC′=2.
故选:D.
7.如图所示,△ABC中,AB=3,AC=2,∠BAC=60°,D是BC的中点,,则=( )
A. B. C. D.
【分析】根据已知条件代入化简,通过向量的数量积的定义求解即可.
解:∵△ABC中,AB=3,AC=2,∠BAC=60°,D是BC的中点,,
∴=()•(﹣)=()•(﹣())=()•(﹣﹣)=﹣﹣﹣=﹣×32﹣×22﹣×3×2×=﹣.
故选:B.
8.欧几里得在《几何原本》中,以基本定义、公设和公理作为全书推理的出发点.其中第Ⅰ命题47是著名的毕达哥拉斯定理(勾股定理),书中给出了一种证明思路:如图,Rt△ABC中,∠BAC=90°,四边形ABHL、ACFG、BCDE都是正方形,AN⊥DE于点N,交BC于点M.先证明△ABE与△HBC全等,继而得到矩形BENM与正方形ABHL面积相等;同理可得到矩形CDNM与正方形ACFG面积相等;进一步推理得证.在该图中,若,则sin∠BEA=( )
A. B. C. D.
【分析】设AB=k,AC=m,BC=n,由勾股定理可得k2+m2=n2,由同角的基本关系式求得sin∠BAE,cos∠BAE,在△ABE中,求得AE,分别运用余弦定理和正弦定理,计算可得所求值.
解:设AB=k,AC=m,BC=n,可得k2+m2=n2,
∵BH∥CL,
∴∠BHC=∠HCL,
又△ABE≅△HBC,
可得∠BHC=∠BAE,
∴∠HCL=∠BAE,
∴,
即,
∴m=k,
∴,
在△ABE中,,得,
在△ABE中,,
即,可得.
故选:D.
二、多项选择题.本大题共4个小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求全部选对得5分,选对但不全的得2分,有选错的得0分.
9.下列各组向量中,可以作为基底的是( )
A.=(0,2),=(,0)
B.=(0,0),=(1,﹣2)
C.=(1,3),=(﹣2,﹣6)
D.=(3,5),=(5,3)
【分析】利用基底的定义,判断两个向量是否共线,即可得到结果.
解:∵0×,∴ 与不共线,∴A正确,
∵0×(﹣2)=0×1,∴ 与共线,∴B错误,
∵1×(﹣6)=3×(﹣2),∴ 与共线,∴C错误,
∵3×3≠5×5,∴ 与不共线,∴D正确,
故选:AD.
10.下列关于复数z的四个命题中假命题为( )
A.若,则z为纯虚数
B.若|z1|=|z2|,则z1=±z2
C.若|z﹣i|=1,则|z|的最大值为2
D.若z3﹣1=0,则z=1
【分析】选项A:设z=a+bi,(a,b为实数),然后求出共轭复数,进而可以判断;选项B:举出反例即可判断,选项C:根据复数的几何意义即可判断,选项D:举出反例即可判断.
解:选项A:设z=a+bi,(a,b为实数),因为,所以z+=2a=0,则a=0,所以z=bi,因为b可能为0,故A错误,
选项B:当z1=1+i,z2=1﹣i时,|z1|=|z2|,故B错误,
选项C:当|z﹣i|=1时,复数z对应的点在以(0,1)为圆心,1为半径的圆上,故|z|的最大值为1+1=2,故C正确,
选项D:当z=﹣时,z3=1,故D错误,
故选:ABD.
11.如图在三棱柱ABC﹣A1B1C1中,CC1⊥底面ABC,AC⊥CB,点D是AB上的动点,则下列结论正确的是( )
A.BC⊥AC1
B.当D为AB的中点时,平面CDB1⊥平面AA1B1B
C.当D为AB中点时,AC1∥平面CDB1
D.三棱锥A1﹣CDB1的体积是定值
【分析】对于A,推导出BC⊥CC1,AC⊥CB,从而BC⊥平面ACC1A1,进而BC⊥AC1;
对于B,当CD⊥AB时,存在点D,使得平面CDB1⊥平面AA1B1B,此时D不一定为中点;
对于C,设BC1∩B1C=O,连结OD,D是AB中点时,OD∥AC1,得AC1∥平面CDB1;
对于D,△A1B1C的面积是定值,由AB∥A1B1,知AB∥平面A1B1C,D到平面A1B1C的距离是定值,进而三棱锥A1﹣CDB1的体积是定值.
解:对于A,∵在三棱柱ABC﹣A1B1C1中,CC1⊥底面ABC,
∴BC⊥CC1,又AC⊥CB,CC1∩CA=C,CC1⊂平面ACC1A1,CB⊂平面ACC1A1,∴BC⊥平面ACC1A1,又AC1⊂平面ACC1A1,∴BC⊥AC1,故A正确;
对于B,∵在三棱柱ABC﹣A1B1C1中,CC1⊥底面ABC,
∴AA1⊥CD,∴当CD⊥AB时,由AA1,AB是平面AA1B1B中的相交线,得到CD⊥平面AA1B1B,平面CDB1⊥平面AA1B1B,此时D不一定为中点,故B错误;
对于C,设BC1∩B1C=O,则O是BC1中点,连结OD,则D是AB中点时,OD∥AC1,
∵AC1⊄平面CDB1,OD⊂平面CDB1,∴AC1∥平面CDB1,故C正确;
对于D,∵△A1B1C的面积是定值,AB∥A1B1,AB⊄平面A1B1C,A1B1⊂平面A1B1C,
∴AB∥平面A1B1C,∴D到平面A1B1C的距离是定值,∴三棱锥A1﹣CDB1的体积是定值,故D正确.
故选:ACD.
12.在△ABC中,内角A,B,C所对的边分别为a,b,c,则下列说法中正确的是( )
A.c=acosB+bcosA
B.若acosA=bcosB,则△ABC为等腰三角形
C.若a2tanB=b2tanA,则a=b
D.若a3+b3=c3,则△ABC为锐角三角形
【分析】由正弦定理以及三角恒等变换可得sinC=sin(A+B)=sinAcosB+sinBcosA,即可判断A;
由正弦定理可将条件转换为sin2A=sin2B,进而得到A=B或A+B=,即可判断B;
由正弦定理把a2tanB=b2tanA转化为:sin2AtanB=sin2BtanA,化简后可判断C;
由a3+b3=c3变形得:()3+()3=1<()2+()²,可判断D;
解:对A:∵sinC=sin(A+B)=sinAcosB+sinBcosA,∴c=acosB+bcosA,所以A正确;
对B:∵acosA=bcosB,∴sinAcosA=sinBcosB,即sin2A=sin2B,
∵△ABC的内角A,B,C,∴2A=2B或2A+2B=π即A=B或A+B=,故三角形可能是等腰三角形或直角三角形,故B错误;
对C:∵a2tanB=b2tanA,∴由正弦定理得:sin2AtanB=sin2BtanA,得:,
整理得:sinAcosA=sinBcosB,∴sin2A=sin2B,∴A=B或A+B=,故C错误;
对D:由题意知:a、b、c中c是最大的正数,∴由a3+b3=c3变形得:()3+()3=1<()2+()²,∴a2+b2>c2,∴C为锐角,又知C为最大角,∴△ABC为锐角三角形,故D正确;
故选:AD.
三、填空题(本题共4个小题,每题5分,共20分)
13.一个口袋中装有2个红球,3个绿球,采用不放回的方式从中依次取出2个球,则第一次取到绿球第二次取到红球的概率为 0.3 .
【分析】根据已知条件,分别求出样本空间的个数和第一次取到绿球第二次取到红球的样本数,再结合古典概型的概率计算公式,即可求解.
解:由题意可得,样本空间的总数为5×4=20,
第一次取到绿球第二次取到红球的样本数为3×2=6,
故所求的概率P=.
故答案为:0.3.
14.在△ABC中,D是BC的中点,AB=1,AC=2,AD=,则△ABC的面积为 .
【分析】根据题意=(),两边平方即可求出=﹣1,从而可求出cos∠BAC=﹣,进而求出sin∠BAC=,然后根据三角形的面积公式即可求出△ABC的面积;
解:∵D是BC中点,且AB=1,AC=2,AD=,
∴=(),则=()²,即=(1+4+2),
∴=﹣1,
∴cos∠BAC===﹣,
∴sin∠BAC=,
∴S△ABC=AB•ACsin∠BAC==.
故答案为:.
15.如图,正方体ABCD﹣A1B1C1D1中,O是AC的中点,直线B1O与平面ACD1所成角的正弦值为 .
【分析】首先建立空间直角坐标系且不妨设正方体ABCD﹣A1B1C1D1的边长为1,于是写出各点的坐标,然后求出
平面ACD1的一个法向量为,进而由sinθ=即可得出所求的答案.
解:以AB、AD、AA1所在的直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
不妨设正方体ABCD﹣A1B1C1D1的边长为1,
则A(0,0,0),B(1,0,0),D(0,1,0),
C(1,1,0),B1(1,0,1),C1(1,1,1),D1(0,1,1),O(,,0),所以=(﹣,,﹣1),
,.
设平面ACD1的一个法向量为,则
,即,令y=﹣1,则x=1=z,则.
于是,===,
所以sinθ=|cos<>|=.
其中θ为直线B1O与平面ACD1所成角.
所以直线B1O与平面ACD1所成角的正弦值为.
故答案为:.
16.如图等腰梯形ABCD中,AB∥CD,,O是梯形ABCD的外接圆的圆心,M是边BC上的中点,则的值为 16 .
【分析】根据题意,利用平面向量的线性运算,即可求解结论.
解:设,
∵M是边BC上的中点,
∴λ=,
则,
又∵,
∴,
∵O是△ABC的外心,
∴,
∴
===,
即,
故答案为:16.
三、解答题:本大题共6个小题,共70分,解答应写出文字说明,证明过程或验算步骤.
17.复数z满足|z|=,z2为纯虚数,若复数z在复平面内所对应的点在第一象限.
(1)求复数z;
(2)复数z,,z2所对应的向量为,,,已知(λ+)⊥(λ+),求λ的值.
【分析】(1)设z=a+bi(a>0,b>0),由已知可得a与b的关系,列方程组求解a与b的最值,则z可求;
(2)由(1)中求得z可得,z2,得到,,,进一步得到(λ+)与(λ+)的坐标,再由数量积为0列式求解λ值.
解:(1)设z=a+bi(a>0,b>0),
则,即a2+b2,①
∵z2=a2﹣b2+2abi为纯虚数,∴a2﹣b2=0且2ab≠0,②
由①②解得a=1,b=1,
∴z=1+i;
(2)∵z=1+i
∴,z2=2i,
∴,
∴,
由,得,
即,
∴4λ﹣2=0,得.
18.△ABC的内角A,B,C的对边分别为a,b,c,已知,
(1)求角A;
(2)若a=,△ABC的面积为,求△ABC的周长.
【分析】(1)由正弦定理可知sinAcosC+sinC=sinB,,结合sinB=sin(A+C)=sinAcosC+cosAsinC,整理即可得到cosA,进而可求出A;
(2)由余弦定理可求得(b+c)2﹣3bc=7,结合面积公式得到bc,进而可知b+c,即可求出周长.
解:(1)∵,
由正弦定理得sinAcosC+sinC=sinB,
又∵sinB=sin(A+C)=sinAcosC+cosAsinC,
∴,
∵sinC>0,
∴,
∴;
(2)由余弦定理得:7=b2+c2﹣2bccos60°即b2+c2﹣bc=7,
∴(b+c)2﹣3bc=7,
又,
∴bc=6,
∴(b+c)2﹣18=7,
∴b+c=5,
∴△ABC的周长为.
19.黄冈市一中学高一年级统计学生本学期20次数学周测成绩(满分150),抽取了甲乙两位同学的20次成绩记录如下:
甲:92,96,99,103,104,105,113,114,117,117,121,123,124,126,129,132,134,136,142,141
乙:102,105,113,114,116,117,125,125,127,128,128,131,131,135,136,138,139,142,145,150
(1)根据以上记录数据求甲乙两位同学成绩的中位数,并据此判断甲乙两位同学的成绩谁更好?
(2)将同学乙的成绩分成[100,110),[120,130)[130,140)[140,150),完成下列频率分布表,并画出频率分布直方图;
(3)现从甲乙两位同学的不低于140分的成绩中任意取出2个成绩,求取出的2个成绩不是同一个人的且没有满分的概率.
分组
频数
频率
[100,110)
[110,120)
[120,130)
[130,140)
[140,150]
合计
20
1
【分析】(1)分别求出甲、乙的中位数,从而得到乙的成绩更好.
(2)完成频率分布表,作出乙的频率分布直方图.
(3)甲乙两位同学的不低于140分的成绩共5个,甲两个成绩记作A1、A2,乙3个成绩记作B1、B2、B3(其中B3表示150分),任意选出2个成绩,利用列举法,求出取出的2个成绩不是同一个人的且没有满分的概率.
解:(1)甲的中位数是=119,
乙的中位数是=128>119,
∴乙的成绩更好.
(2)完成频率分布表如下:
分组
频数
频率
[100,110)
2
0.1
[110,120)
4
0.2
[120,130)
5
0.25
[130,140)
6
0.3
[140,150)
3
0.15
合计
20
1
乙的频率分布直方图如下图所示:
(3)甲乙两位同学的不低于140(分)的成绩共5个,甲两个成绩记作A1、A2,
乙3个成绩记作B1、B2、B3(其中B3表示150分),
任意选出2个成绩所有的取法为:
(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),
(A2,B3),(B1,B2),(B1,B3),(B2,B3),共10种取法,
其中两个成绩不是同一个人的且没有满分的是:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),共4种取法,
∴取出的2个成绩不是同一个人的且没有满分的概率P=.
20.如图,已知在四棱锥P﹣ABCD中,底面ABCD是梯形,BC∥AD且BC=2AD,平面PAC⊥平面ABCD,PA=PC,PA⊥AB.
(1)证明:AB⊥PC;
(2)若PA⊥PC,PB=2PC=4,求四棱锥P﹣ABCD的体积.
【分析】(1)取AC的中点O,连接PO,得出PO⊥AC,根据平面PAC⊥平面ABCD得出PO⊥平面ABCD,证明PO⊥AB;再由AB⊥PA证明AB⊥平面PAC,即可证明AB⊥PC.
(2)根据题意利用分割补形法计算四棱锥P﹣ABCD的体积,另一种解法是直接计算四棱锥的体积即可.
【解答】(1)证明:取AC的中点O,连接PO,如图所示;
因为AP=PC,所以PO⊥AC,
又因为平面PAC⊥平面ABCD,所以PO⊥平面ABCD,
又因为AB⊂平面ABCD,所以PO⊥AB;......①
又因为AB⊥PA,......②
由①②可得AB⊥平面PAC,所以AB⊥PC.
(2)解:因为PB=2PC=4,所以PA=PC=2,
又AB⊥PA,所以AB2=PB2﹣PA2,所以;
又因为PA⊥PC,PA=PC=2,所以,;
由(1)知AB⊥平面PAC,所以AB⊥AC,
所以;
所以;
又因为BC//AD,BC=2AD,所以S△ABC=2S△ACD,
所以;
所以四棱锥P﹣ABCD的体积是
.
另解:因为,
所以,所以,
计算四棱锥P﹣ABCD的体积是.
21.如图,四边形ABCD中,∠BAC=90°,∠ABC=60°,AD⊥CD,设∠ACD=θ.
(1)若△ABC面积是△ACD面积的4倍,求sin2θ;
(2)若tan∠ADB=,求tanθ.
【分析】(1)直接利用三角形的面积公式的应用求出结果;
(2)利用正弦定理建立方程组,进一步建立三角函数式,最后解方程组求出结果.
解:(1)设AB=a,
则,,,
由题意S△ABC=4S△ACD,
则,
所以.
(2)由正弦定理,△ABD中,,
即①
在△BCD中,,
即②
②÷①得:,
∴,
化简得,
所以.
22.如图①梯形ABCD中AD∥BC,AB=,BC=1,,BE⊥AD且BE=1,将梯形沿BE折叠得到图②,使平面ABE⊥平面BCDE,CE与BD相交于O,点P在AB上,且AP=2PB,R是CD的中点,过O,P,R三点的平面交AC于Q.
(1)证明:Q是的中点;
(2)证明:AD⊥平面BEQ;
(3)M是AB上一点,已知二面角M﹣EC﹣B为45°,求的值.
【分析】(1)在图①中过C作CF⊥AD,证明PQ∥AD,结合R是CD的中点,推出Q是AC的中点.
(2)证明CD⊥CE,推出AE⊥CD,得到CD⊥平面ACE,推出CD⊥EQ,EQ⊥AC,即可证明EQ⊥平面ACD,得到EQ⊥AD,推出BE⊥AD然后证明AD⊥平面BEQ.
(3)过M作MH⊥BE,过H作HG⊥CE,连结MG,说明∠MGH为二面角M﹣CE﹣B的平面角,设,然后转化求解即可.
【解答】证明:(1)在图①中过C作CF⊥AD,
则EF=BC=1,CF=BE=1,
又∵,∴DF=1,∴DE=2,∴DE∥BC,且DE=2BC,∴DO=2OB,
又∵AP=2PB,∴OP∥AD,∴OP∥平面ACD,
又∵平面OPQR∩平面ACD=RQ,∴OP∥RQ,∴PQ∥AD,
又∵R是CD的中点,∴Q是AC的中点.
(2)在直角梯形BCDE中,BC=BE=1,
∴,∴∠CED=∠BCE=45°.
又,∴∠ECD=90°,DE=2,∴CD⊥CE,①
又∵平面ABE⊥平面BCDE,AE⊥BE,∴AE⊥平面BCDE,∴AE⊥CD,②
由①②得CD⊥平面ACE,∴CD⊥EQ,③
∵,∴,∴AE=CE,∴EQ⊥AC,④
由③④可得EQ⊥平面ACD,∴EQ⊥AD,⑤
又∵BE⊥AE,BE⊥DE,∴BE⊥平面ADE,∴BE⊥AD,⑥
由⑤⑥可得AD⊥平面BEQ.
(3)过M作MH⊥BE,则MH⊥平面BCDE,
过H作HG⊥CE,连结MG,
则∠MGH为二面角M﹣CE﹣B的平面角,∴∠MGH=45°,
设,∴,
又,∴HE=λ,∵∠BEC=45°,∴,
由∠MGH=45°得HG=MH,
∴,
∴.
2022-2023学年湖北省黄冈市圆创高三年级调研考试数学试卷及答案: 这是一份2022-2023学年湖北省黄冈市圆创高三年级调研考试数学试卷及答案,共19页。
2020-2021学年湖北省黄冈市高一(下)期末数学试卷: 这是一份2020-2021学年湖北省黄冈市高一(下)期末数学试卷,共25页。试卷主要包含了单项选择题,填空题等内容,欢迎下载使用。
湖北省新高考联考协作体2020-2021学年高一下学期期末考试数学试卷: 这是一份湖北省新高考联考协作体2020-2021学年高一下学期期末考试数学试卷,文件包含2021年湖北省新高考联考协作体高一下学期期末联考数学答案docx、2021年湖北省新高考联考协作体高一下学期期末考试--高一数学试卷pdf等2份试卷配套教学资源,其中试卷共11页, 欢迎下载使用。












