初中数学沪科版九年级上册23.1 锐角的三角函数第1课时教学设计

这是一份初中数学沪科版九年级上册23.1 锐角的三角函数第1课时教学设计，共5页。教案主要包含了知识与技能，过程与方法，情感、态度与价值观等内容，欢迎下载使用。

教学目标
【知识与技能】
1.熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应的锐角度数.
2.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
【过程与方法】
1.培养学生把实际问题转化为数学问题的能力.
2.培养学生观察、比较、分析、概括的能力.
【情感、态度与价值观】
经历观察、操作、归纳等学习数学的过程,感受数学思考过程的合理性,感受数学说理的必要性、说理过程的严谨性,养成科学、严谨的学习态度.
重点难点
【重点】
30°、45°、60°角的三角函数值.
【难点】
与特殊角的三角函数值有关的计算.
教学进程
一、复习巩固
教师多媒体课件出示:
如图所示:在Rt△ABC中,∠C=90°.
(1)a、b、c三者之间的关系是 ;
(2)sinA= ,csA= ,
tanA= ;
sinB= ,csB= ,
tanB= .
(3)若∠A=30°,则= .
学生回答.
二、共同探究,获取新知
1.引出新知
教师多媒体课件出示问题:
为了测量一棵大树的高度,准备了如下测量工具:(1)含30°和60°两个锐角的三角尺;(2)皮尺.请你设计一个测量方案,测出一棵大树的高度.
学生讨论,交流想法.
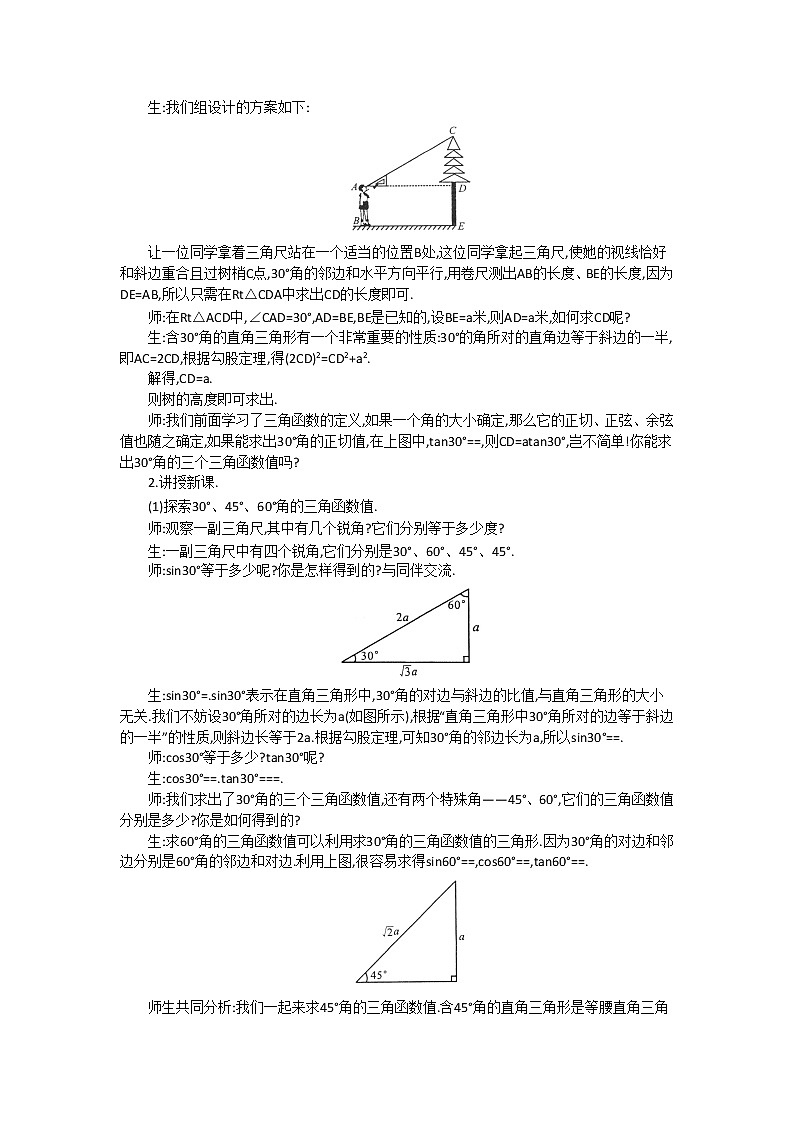
生:我们组设计的方案如下:
让一位同学拿着三角尺站在一个适当的位置B处,这位同学拿起三角尺,使她的视线恰好和斜边重合且过树梢C点,30°角的邻边和水平方向平行,用卷尺测出AB的长度、BE的长度,因为DE=AB,所以只需在Rt△CDA中求出CD的长度即可.
师:在Rt△ACD中,∠CAD=30°,AD=BE,BE是已知的,设BE=a米,则AD=a米,如何求CD呢?
生:含30°角的直角三角形有一个非常重要的性质:30°的角所对的直角边等于斜边的一半,即AC=2CD,根据勾股定理,得(2CD)2=CD2+a2.
解得,CD=a.
则树的高度即可求出.
师:我们前面学习了三角函数的定义,如果一个角的大小确定,那么它的正切、正弦、余弦值也随之确定,如果能求出30°角的正切值,在上图中,tan30°==,则CD=atan30°,岂不简单!你能求出30°角的三个三角函数值吗?
2.讲授新课.
(1)探索30°、45°、60°角的三角函数值.
师:观察一副三角尺,其中有几个锐角?它们分别等于多少度?
生:一副三角尺中有四个锐角,它们分别是30°、60°、45°、45°.
师:sin30°等于多少呢?你是怎样得到的?与同伴交流.
生:sin30°=.sin30°表示在直角三角形中,30°角的对边与斜边的比值,与直角三角形的大小无关.我们不妨设30°角所对的边长为a(如图所示),根据“直角三角形中30°角所对的边等于斜边的一半”的性质,则斜边长等于2a.根据勾股定理,可知30°角的邻边长为a,所以sin30°==.
师:cs30°等于多少?tan30°呢?
生:cs30°==.tan30°===.
师:我们求出了30°角的三个三角函数值,还有两个特殊角——45°、60°,它们的三角函数值分别是多少?你是如何得到的?
生:求60°角的三角函数值可以利用求30°角的三角函数值的三角形.因为30°角的对边和邻边分别是60°角的邻边和对边.利用上图,很容易求得sin60°==,cs60°==,tan60°==.
师生共同分析:我们一起来求45°角的三角函数值.含45°角的直角三角形是等腰直角三角形.如图,设其中一条直角边为a,则另一条直角边也为a,斜边为a.由此可求得
sin45°===,
cs45°===,
tan45°==1.
教师多媒体课件出示:
师:这个表格中的30°、45°、60°角的三角函数值需要熟记.另一方面,要能够根据30°、45°、60°角的三角函数值说出相应的锐角的大小.
为了帮助大家记忆,我们观察表格中函数值的特点.先看第一列30°、45°、60°角的正弦值,你能发现什么规律呢?
生:30°、45°、60°角的正弦值分母都为2,分子从小到大分别为、、,随着角度的增大,正弦值在逐渐增大.
师:再来看第二列的函数值,有何特点呢?
生:第二列是30°、45°、60角的余弦值,它们的分母也都是2,而分子从小到大分别为、、,余弦值随角度的增大而减小.
师:第三列呢?
生:第三列是30°、45°、60°角的正切值,首先45°角是等腰直角三角形中的一个锐角,所以tan45°=1比较特殊.
师:很好!掌握了上述规律,记忆就方便多了.下面同桌之间可互相检查一下对30°、45°、60°角的三角函数值的记忆情况.相信同学们一定会做得很棒!
(2)进一步探究锐角的三角函数值.
如图,在Rt△ABC中,∠C=90°.
∵sinA=,csA=,
sinB=,csB=,
∴sinA=csB,csA=sinB.
∵∠A+∠B=90°,
∴∠B=90-∠A,
即 sinA=csB=cs(90°-∠A),
csA=sinB=sin(90°-∠A).
任意一个锐角的正(余)弦值,等于它的余角的余(正)弦值.
三、例题讲解,巩固新知
【例1】 计算:
(1)sin30°+cs45°;
(2)sin260°+cs260°-tan45°.
分析:本题旨在帮助学生巩固特殊角的三角函数值,今后若无特别说明,用特殊角的三角函数值进行计算时,一般不取近似值,另外sin260°表示(sin60°)2,cs260°表示(cs60°)2;
教师找两生板演,其余同学在下面做,然后集体订正得到:
解:(1)sin30°+cs45°=+=;
(2)sin260°+cs260°-tan45°
=()2+()2-1
=+-1
=0.
【例2】 在Rt△ABC中,∠C=90°,且sinA=,求csB的值.
解:∵∠A+∠B=90°,∴csB=cs(90°-∠A)
=sinA=.
【例3】 一个小孩荡秋千,秋千链子的长度为2.5 m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差.(结果精确到0.01 m)
分析:引导学生自己根据题意画出示意图,培养学生把实际问题转化为数学问题的能力.
解:根据题意(如图)可知,
∠BOD=60°,
OB=OA=OD=2.5 m,
∠AOD=×60°=30°,
∴OC=OD·cs30°
=2.5×≈2.165(m).
∴AC=2.5-2.165≈0.34(m).
所以,最高位置与最低位置的高度差约为0.34 m.
四、随堂练习
师:同学们,刚才学习了那么多,现在让我来检测一下你们学得怎么样了.
教师多媒体课件出示:
1.sin30°的值为( )
A. B. C. D.
【答案】C
2.计算4sin60°-3tan30°的值为( )
A.B.2C.3D.0
【答案】A
3.计算sin245°+cs245°的值为( )
A.2B.1C.0D.3
【答案】B
4.计算的值为( )
A.1-B.-1C.-1D.1-
【答案】A
5.下列各式中,正确的是( )
A.sin20°+sin55°=sin75°
B.tan80°-tan50°=tan30°
C.2cs60°=1
D.cs60°-cs30°=cs30°
【答案】C
6.计算:
(1)sin60°-tan45°;
(2)cs60°+tan60°;
(3)sin45°+sin60°-2cs45°.
【答案】(1)原式=-1=;
(2)原式=+=;
(3)原式=×+-2×=.
7.某商场有一自动扶梯,其倾斜角为30°,高为7 m.扶梯的长度是多少?
【答案】扶梯的长度为==14(m),
所以扶梯的长度为14 m.
五、课堂小结
本节课总结如下:
1.探索30°、45°、60°角的三角函数值.
sin30°=,sin45°=,sin60°=;
cs30°=,cs45°=,cs60°=;
tan30°=,tan45°=1,tan60°=.
2.能进行含30°、45°、60°角的三角函数值的计算.
3.能根据30°、45°、60°角的三角函数值,说出相应锐角的大小.
教学反思
本节课的教学中,课堂环节设置齐全,能很好地贯彻执行理解教育,对理解教育的教育模式把控较好;课堂中学生分组很好,能给学生构建一个宽松、和谐的学习环境和氛围;课件制作很好,能很好的配合指导自学书的使用,提高了课堂的效率;学生积极参与,学习积极性较高;课堂习题的设置有梯度,题目能面向全体学生.
三角函数
角度α
sinα
csα
tanα
30°
45°
1
60°