

05解答题(中档题)-四川省南充市五年(2018-2022)中考数学真题分类汇编(共20题)
展开这是一份05解答题(中档题)-四川省南充市五年(2018-2022)中考数学真题分类汇编(共20题),共30页。
05解答题-四川省南充市五年(2018-2022)中考数学真题分类汇编
一、 全等三角形的判定与性质(共4小题)
1. (2020•南充)如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.
2. (2021•南充)如图,∠BAC=90°,AD是∠BAC内部一条射线,若AB=AC,BE⊥AD于点E,CF⊥AD于点F.求证:AF=BE.
3. (2019•南充)如图,点O是线段AB的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠ADO=35°,求∠DOC的度数.
4. (2018•南充)如图,已知AB=AD,AC=AE,∠BAE=∠DAC.
求证:∠C=∠E.
二、 菱形的性质(共1小题)
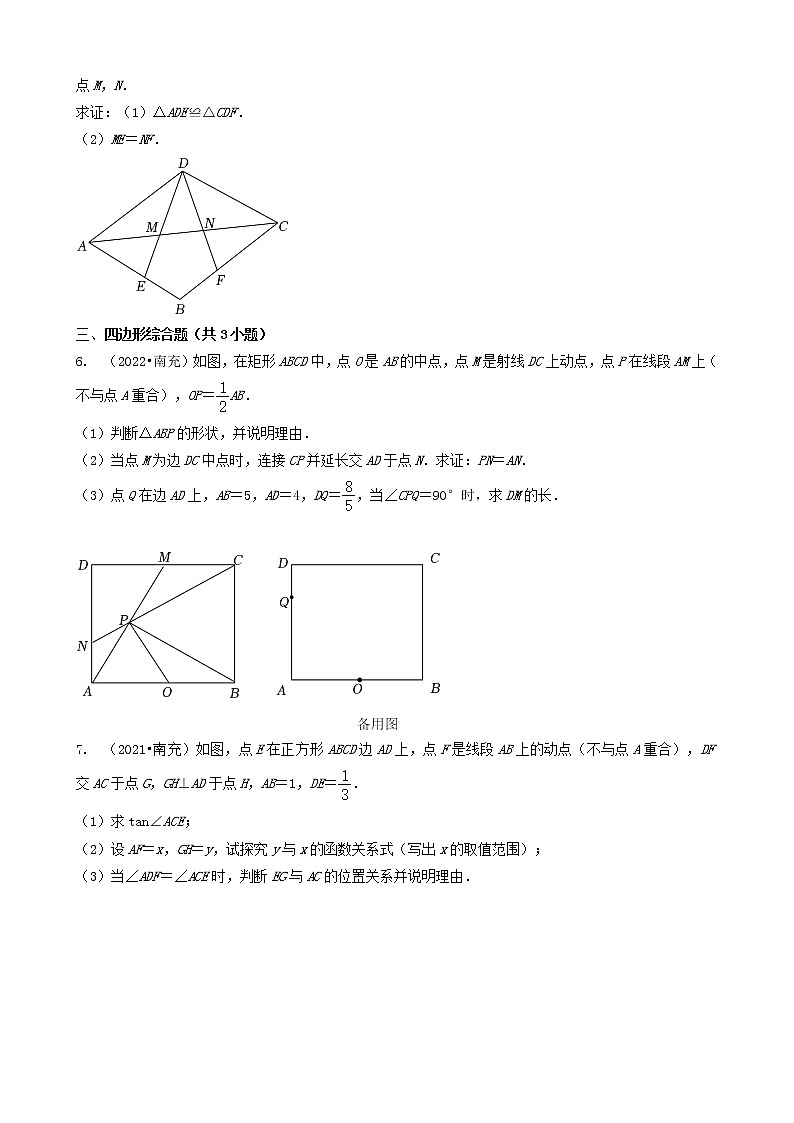
5. (2022•南充)如图,在菱形ABCD中,点E,F分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.
求证:(1)△ADE≌△CDF.
(2)ME=NF.
三、 四边形综合题(共3小题)
6. (2022•南充)如图,在矩形ABCD中,点O是AB的中点,点M是射线DC上动点,点P在线段AM上(不与点A重合),OP=AB.
(1)判断△ABP的形状,并说明理由.
(2)当点M为边DC中点时,连接CP并延长交AD于点N.求证:PN=AN.
(3)点Q在边AD上,AB=5,AD=4,DQ=,当∠CPQ=90°时,求DM的长.
7. (2021•南充)如图,点E在正方形ABCD边AD上,点F是线段AB上的动点(不与点A重合),DF交AC于点G,GH⊥AD于点H,AB=1,DE=.
(1)求tan∠ACE;
(2)设AF=x,GH=y,试探究y与x的函数关系式(写出x的取值范围);
(3)当∠ADF=∠ACE时,判断EG与AC的位置关系并说明理由.
8. (2020•南充)如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.
(1)求证:AM=BN.
(2)请判定△OMN的形状,并说明理由.
(3)若点K在线段AD上运动(不包括端点),设AK=x,△OMN的面积为y,求y关于x的函数关系式(写出x的范围);若点K在射线AD上运动,且△OMN的面积为,请直接写出AK长.
四、 直线与圆的位置关系(共1小题)
9. (2020•南充)如图,点A,B,C是半径为2的⊙O上三个点,AB为直径,∠BAC的平分线交圆于点D,过点D作AC的垂线交AC的延长线于点E,延长ED交AB的延长线于点F.
(1)判断直线EF与⊙O的位置关系,并证明.
(2)若DF=4,求tan∠EAD的值.
五、 切线的判定与性质(共4小题)
10. (2022•南充)如图,AB为⊙O的直径,点C是⊙O上一点,点D是⊙O外一点,∠BCD=∠BAC,连接OD交BC于点E.
(1)求证:CD是⊙O的切线.
(2)若CE=OA,sin∠BAC=,求tan∠CEO的值.
11. (2021•南充)如图,A,B是⊙O上两点,且AB=OA,连接OB并延长到点C,使BC=OB,连接AC.
(1)求证:AC是⊙O的切线;
(2)点D,E分别是AC,OA的中点,DE所在直线交⊙O于点F,G,OA=4,求GF的长.
12. (2019•南充)如图,在△ABC中,以AC为直径的⊙O交AB于点D,连接CD,∠BCD=∠A.
(1)求证:BC是⊙O的切线;
(2)若BC=5,BD=3,求点O到CD的距离.
13. (2018•南充)如图,C是⊙O上一点,点P在直径AB的延长线上,⊙O的半径为3,PB=2,PC=4.
(1)求证:PC是⊙O的切线.
(2)求tan∠CAB的值.
六、 旋转的性质(共1小题)
14. (2018•南充)如图,矩形ABCD中,AC=2AB,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B'落在AC上,B'C'交AD于点E,在B'C′上取点F,使B'F=AB.
(1)求证:AE=C′E.
(2)求∠FBB'的度数.
(3)已知AB=2,求BF的长.
七、 相似形综合题(共1小题)
15. (2019•南充)如图,在正方形ABCD中,点E是AB边上一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM交GF于点H,EF与CB交于点N,连接CG.
(1)求证:CD⊥CG;
(2)若tan∠MEN=,求的值;
(3)已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为?请说明理由.
八、 列表法与树状图法(共5小题)
16. (2022•南充)为传播数学文化,激发学生学习兴趣,学校开展数学学科月活动,七年级开展了四个项目:A.阅读数学名著;B.讲述数学故事;C.制作数学模型;D.挑战数学游戏.要求七年级学生每人只能参加一项.为了解学生参加各项目情况,随机调查了部分学生,将调查结果制作成统计表和扇形统计图(如图),请根据图表信息解答下列问题:
项目
A
B
C
D
人数/人
5
15
a
b
(1)a= ,b= .
(2)扇形统计图中“B”项目所对应的扇形圆心角为 度.
(3)在月末的展示活动中,“C”项目中七(1)班有3人获得一等奖,七(2)班有2人获得一等奖,现从这5名学生中随机抽取2人代表七年级参加学校制作数学模型比赛,请用列表或画树状图法求抽中的2名学生来自不同班级的概率.
17. (2021•南充)某市体育中考自选项目有乒乓球、篮球和羽毛球,每个考生任选一项作为自选考试项目.
(1)求考生小红和小强自选项目相同的概率;
(2)除自选项目之外,长跑和掷实心球为必考项目.小红和小强的体育中考各项成绩(百分制)的统计图表如下:
考生
自选项目
长跑
掷实心球
小红
95
90
95
小强
90
95
95
①补全条形统计图.
②如果体育中考按自选项目占50%、长跑占30%、掷实心球占20%计算成绩(百分制),分别计算小红和小强的体育中考成绩.
18. (2019•南充)现有四张完全相同的不透明卡片,其正面分别写有数字﹣2,﹣1,0,2,把这四张卡片背面朝上洗匀后放在桌面上.
(1)随机地取一张卡片,求抽取的卡片上的数字为负数的概率.
(2)先随机抽取一张卡片,其上的数字作为点A的横坐标;然后放回并洗匀,再随机抽取一张卡片,其上的数字作为点A的纵坐标,试用画树状图或列表的方法求出点A在直线y=2x上的概率.
19. (2020•南充)今年,全球疫情大爆发,我国派遣医疗专家组对一些国家进行医疗援助.某批次派出20人组成的专家组,分别赴A、B、C、D四个国家开展援助工作,其人员分布情况如统计图(不完整)所示:
(1)计算赴B国女专家和D国男专家人数,并将条形统计图补充完整.
(2)根据需要,从赴A国的专家中,随机抽取两名专家对当地医疗团队进行培训,求所抽取的两名专家恰好是一男一女的概率.
20. (2018•南充)“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分
7
8
9
10
人数/人
2
5
4
4
(1)这组数据的众数是 ,中位数是 .
(2)已知获得10分的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
参考答案与试题解析
一、 全等三角形的判定与性质(共4小题)
1. (2020•南充)如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.
【解答】证明:∵AB⊥BD,ED⊥BD,AC⊥CE,
∴∠ACE=∠ABC=∠CDE=90°,
∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,
∴∠ACB=∠CED.
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA),
∴AB=CD.
2. (2021•南充)如图,∠BAC=90°,AD是∠BAC内部一条射线,若AB=AC,BE⊥AD于点E,CF⊥AD于点F.求证:AF=BE.
【解答】证明:∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∵BE⊥AD,CF⊥AD,
∴∠BEA=∠AFC=90°,
∴∠BAE+∠EBA=90°,
∴∠EBA=∠FAC,
在△ACF和△BAE中,
,
∴△ACF≌△BAE(AAS),
∴AF=BE.
3. (2019•南充)如图,点O是线段AB的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠ADO=35°,求∠DOC的度数.
【解答】(1)证明:∵点O是线段AB的中点,
∴AO=BO,
∵OD∥BC,
∴∠AOD=∠OBC,
在△AOD与△OBC中,,
∴△AOD≌△OBC(SAS);
(2)解:∵△AOD≌△OBC,
∴∠ADO=∠OCB=35°,
∵OD∥BC,
∴∠DOC=∠OCB=35°.
4. (2018•南充)如图,已知AB=AD,AC=AE,∠BAE=∠DAC.
求证:∠C=∠E.
【解答】证明:∵∠BAE=∠DAC,
∴∠BAE﹣∠CAE=∠DAC﹣∠CAE,即∠BAC=∠DAE,
在△ABC和△ADE中,
∵,
∴△ABC≌△ADE(SAS),
∴∠C=∠E.
二、 菱形的性质(共1小题)
5. (2022•南充)如图,在菱形ABCD中,点E,F分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.
求证:(1)△ADE≌△CDF.
(2)ME=NF.
【解答】证明:(1)∵四边形ABCD是菱形,
∴DA=DC,∠DAE=∠DCF,AB=CB,
∵BE=BF,
∴AE=CF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS);
(2)由(1)知△ADE≌△CDF,
∴∠ADM=∠CDN,DE=DF,
∵四边形ABCD是菱形,
∴∠DAM=∠DCN,
∴∠DMA=∠DNC,
∴∠DMN=∠DNM,
∴DM=DN,
∴DE﹣DM=DF﹣DN,
∴ME=NF.
三、 四边形综合题(共3小题)
6. (2022•南充)如图,在矩形ABCD中,点O是AB的中点,点M是射线DC上动点,点P在线段AM上(不与点A重合),OP=AB.
(1)判断△ABP的形状,并说明理由.
(2)当点M为边DC中点时,连接CP并延长交AD于点N.求证:PN=AN.
(3)点Q在边AD上,AB=5,AD=4,DQ=,当∠CPQ=90°时,求DM的长.
【解答】(1)解:△ABP是直角三角形,理由如下:
∵点O是AB的中点,
∴AO=OB=AB,
∵OP=AB,
∴OP=OA=OB,
∴∠OBP=∠OPB,∠OAP=∠APO,
∵∠OAP+∠APO+∠OBP+∠BPO=180°,
∴∠APO+∠BPO=90°,
∴∠APB=90°,
∴△ABP是直角三角形;
(2)证明:如图1,延长AM,BC交于点Q,
∵M是CD的中点,
∴DM=CM,
∵∠D=∠MCQ=90°,∠AMD=∠QMC,
∴△ADM≌△QCM(ASA),
∴AD=CQ=BC,
∵∠BPQ=90°,
∴PC=BQ=BC,
∴∠CPB=∠CBP,
∵∠OPB=∠OBP,
∴∠OBC=∠OPC=90°,
∴∠OPN=∠OPA+∠APN=90°,
∵∠OAP+∠PAN=90°,∠OAP=∠OPA,
∴∠APN=∠PAN,
∴PN=AN;
(3)解:分两种情况:
①如图2,点M在CD上时,过点P作GH∥CD,交AD于G,交BC于H,
设DM=x,QG=a,则CH=a+,BH=AG=4﹣﹣a=﹣a,
∵PG∥DM,
∴△AGP∽△ADM,
∴=,即,
∴PG=x﹣ax,
∵∠CPQ=90°,
∴∠CPH+∠QPG=90°,
∵∠CPH+∠PCH=90°,
∴∠QPG=∠PCH,
∴tan∠QPG=tan∠PCH,即=,
∴PH•PG=QG•CH,
同理得:∠APG=∠PBH,
∴tan∠APG=tan∠PBH,即=,
∴PG•PH=AG•BH=AG2,
∴AG2=QG•CH,即(﹣a)2=a(+a),
∴a=,
∵PG•PH=AG2,
∴(x﹣x)•(5﹣x+x)=(﹣)2,
解得:x1=12(舍),x2=,
∴DM=;
②如图3,当M在DC的延长线上时,同理得:DM=12,
综上,DM的长是或12.
7. (2021•南充)如图,点E在正方形ABCD边AD上,点F是线段AB上的动点(不与点A重合),DF交AC于点G,GH⊥AD于点H,AB=1,DE=.
(1)求tan∠ACE;
(2)设AF=x,GH=y,试探究y与x的函数关系式(写出x的取值范围);
(3)当∠ADF=∠ACE时,判断EG与AC的位置关系并说明理由.
【解答】解:(1)过点E作EM⊥AC于点M,
∴∠AME=∠EMC=90°,
∵四边形ABCD是边长为1的正方形,DE=,
∴∠CAD=45°,AE=AD﹣DE=1﹣=,
∴EM=AM=AE•sin∠CAD=,AC=,
∴CM=AC﹣AM=﹣=,
∴tan∠ACE===;
(2)∵GH⊥AD,AB⊥AD,
∴GH∥AB,
∴△DHG∽△DAF,
∴,
∴,
∴y=x﹣xy,
∴y=(0<x≤1);
(3)当∠ADF=∠ACE时,EG⊥AC,
理由如下:
∵tan∠ADF=tan∠ACE=,
∴,
∴x=,y=,
∴HA=GH=,
∴EH=AD﹣DE﹣AH=,
∴EG===,
∴EG=EM,
又∵EM⊥AC,
∴点G与点M重合,
∴EG⊥AC.
8. (2020•南充)如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.
(1)求证:AM=BN.
(2)请判定△OMN的形状,并说明理由.
(3)若点K在线段AD上运动(不包括端点),设AK=x,△OMN的面积为y,求y关于x的函数关系式(写出x的范围);若点K在射线AD上运动,且△OMN的面积为,请直接写出AK长.
【解答】证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABM+∠CBM=90°,
∵AM⊥BM,CN⊥BN,
∴∠AMB=∠BNC=90°,
∴∠MAB+∠MBA=90°,
∴∠MAB=∠CBM,
∴△ABM≌△BCN(AAS),
∴AM=BN;
(2)△OMN是等腰直角三角形,
理由如下:如图,连接OB,
∵点O是正方形ABCD的中心,
∴OA=OB,∠OBA=∠OAB=45°=∠OBC,AO⊥BO,
∵∠MAB=∠CBM,
∴∠MAB﹣∠OAB=∠CBM﹣∠OBC,
∴∠MAO=∠NBO,
又∵AM=BN,OA=OB,
∴△AOM≌△BON(SAS),
∴MO=NO,∠AOM=∠BON,
∵∠AON+∠BON=90°,
∴∠AON+∠AOM=90°,
∴∠MON=90°,
∴△MON是等腰直角三角形;
(3)在Rt△ABK中,BK==,
∵S△ABK=×AK×AB=×BK×AM,
∴AM==,
∴BN=AM=,
∵cos∠ABK==,
∴BM==,
∴MN=BM﹣BN=
∵S△OMN=MN2=,
∴y=(0<x<1);
当点K在线段AD上时,则=,
解得:x1=3(不合题意舍去),x2=,
当点K在线段AD的延长线时,同理可求y=(x>1),
∴=,
解得:x1=3,x2=(不合题意舍去),
综上所述:AK的值为3或时,△OMN的面积为.
四、 直线与圆的位置关系(共1小题)
9. (2020•南充)如图,点A,B,C是半径为2的⊙O上三个点,AB为直径,∠BAC的平分线交圆于点D,过点D作AC的垂线交AC的延长线于点E,延长ED交AB的延长线于点F.
(1)判断直线EF与⊙O的位置关系,并证明.
(2)若DF=4,求tan∠EAD的值.
【解答】解:(1)直线EF与⊙O相切,
证明:连接OD,如图所示:
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠EAF,
∴∠DAE=∠DAO,
∴∠DAE=∠ADO,
∴OD∥AE,
∵AE⊥EF,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)在Rt△ODF中,OD=2,DF=4,
∴OF==6,
∵OD∥AE,
∴,
∴==,
∴AE=,ED=,
∴tan∠EAD==.
五、 切线的判定与性质(共4小题)
10. (2022•南充)如图,AB为⊙O的直径,点C是⊙O上一点,点D是⊙O外一点,∠BCD=∠BAC,连接OD交BC于点E.
(1)求证:CD是⊙O的切线.
(2)若CE=OA,sin∠BAC=,求tan∠CEO的值.
【解答】(1)证明:连接OC,
∵AB是直径,
∴∠ACB=90°,
∴∠A+∠B=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∵∠BCD=∠BAC,
∴∠OCB+∠DCB=90°,
∴OC⊥CD,
∵OC为⊙O的半径,
∴CD是⊙O的切线;
(2)解:过点O作OH⊥BC于点H.
∵sin∠BAC==,
∴可以假设BC=4k,AB=5k,则AO=OC=CE=2.5k,
∵OH⊥BC,
∴CH=BH=2k,
∵OA=OB,
∴OH=AC=k,
∴EH=CE﹣CH=2.5k﹣2k=0.5k,
∴tan∠CEO===3.
11. (2021•南充)如图,A,B是⊙O上两点,且AB=OA,连接OB并延长到点C,使BC=OB,连接AC.
(1)求证:AC是⊙O的切线;
(2)点D,E分别是AC,OA的中点,DE所在直线交⊙O于点F,G,OA=4,求GF的长.
【解答】(1)证明:∵AB=OA=OB,
∴△OAB是等边三角形.
∴∠AOB=∠OBA=∠OAB=60°.
∵BC=OB,
∴BC=AB,
∴∠BAC=∠C,
∵∠OBA=∠BAC+∠C=60°,
∴∠BAC=∠C=30°.
∴∠OAC=∠OAB+∠BAC=90°.
∴OA⊥AC,
∵点A在⊙O上,
∴AC是⊙O的切线;
(2)解:如图,连结OF,过点O作OH⊥GF于点H.
∴GF=2HF,∠OHE=∠OHF=90°.
∵点D,E分别是AC,OA的中点,
∴OE=AE=OA=×4=2,DE∥OC.
∴∠OEH=∠AOB=60°,OH=OEsin∠OEH=.
∴HF===.
∴GF=2HF=2.
12. (2019•南充)如图,在△ABC中,以AC为直径的⊙O交AB于点D,连接CD,∠BCD=∠A.
(1)求证:BC是⊙O的切线;
(2)若BC=5,BD=3,求点O到CD的距离.
【解答】(1)证明:∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∵∠BCD=∠A,
∴∠ACD+∠BCD=90°,
∴∠ACB=90°,
∴BC是⊙O的切线;
(2)解:过O作OH⊥CD于H,
∵∠BDC=∠ACB=90°,∠B=∠B,
∴△ACB∽△CDB,
∴=,
∴=,
∴AB=,
∴AD=,
∵OH⊥CD,
∴CH=DH,
∵AO=OC,
∴OH=AD=,
∴点O到CD的距离是.
13. (2018•南充)如图,C是⊙O上一点,点P在直径AB的延长线上,⊙O的半径为3,PB=2,PC=4.
(1)求证:PC是⊙O的切线.
(2)求tan∠CAB的值.
【解答】解:(1)如图,连接OC、BC
∵⊙O的半径为3,PB=2
∴OC=OB=3,OP=OB+PB=5
∵PC=4
∴OC2+PC2=OP2
∴△OCP是直角三角形,
∴OC⊥PC
∴PC是⊙O的切线.
(2)∵AB是直径
∴∠ACB=90°
∴∠ACO+∠OCB=90°
∵OC⊥PC
∴∠BCP+∠OCB=90°
∴∠BCP=∠ACO
∵OA=OC
∴∠A=∠ACO
∴∠A=∠BCP
在△PBC和△PCA中:
∠BCP=∠A,∠P=∠P
∴△PBC∽△PCA,
∴
∴tan∠CAB=
六、 旋转的性质(共1小题)
14. (2018•南充)如图,矩形ABCD中,AC=2AB,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B'落在AC上,B'C'交AD于点E,在B'C′上取点F,使B'F=AB.
(1)求证:AE=C′E.
(2)求∠FBB'的度数.
(3)已知AB=2,求BF的长.
【解答】(1)证明:∵在Rt△ABC中,AC=2AB,
∴∠ACB=∠AC′B′=30°,∠BAC=60°,
由旋转可得:AB′=AB,∠B′AC′=∠BAC=60°,
∴∠EAC′=∠AC′B′=30°,
∴AE=C′E;
(2)解:由(1)得到△ABB′为等边三角形,
∴∠AB′B=60°,即∠BB'F=∠AB'B+∠AB'F=150°,
∵BB'=B'F,
∴∠FBB′=∠B'FB=15°;
(3)法1:解:由AB=2,得到B′B=B′F=2,∠B′BF=15°,
过B作B′H⊥BF,
在Rt△BB′H中,cos15°=,
∵cos15°=cos(45°﹣30°)=cos45°cos30°+sin45°sin30°=×+×=,
∴BH=2×=,
∴BF=2BH=+.
法2:连接AF,过A作AM⊥BF,
由(2)可得△AB′F是等腰直角三角形,△AB′B为等边三角形,
∴∠AFB′=45°,
∴∠AFM=30°,∠ABF=45°,
在Rt△ABM中,AM=BM=AB•cos∠ABM=2×=,
在Rt△AMF中,MF===,
则BF=+.
七、 相似形综合题(共1小题)
15. (2019•南充)如图,在正方形ABCD中,点E是AB边上一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM交GF于点H,EF与CB交于点N,连接CG.
(1)求证:CD⊥CG;
(2)若tan∠MEN=,求的值;
(3)已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为?请说明理由.
【解答】(1)证明:∵四边形ABCD和四边形DEFG是正方形,
∴∠A=∠ADC=∠EDG=90°,AD=CD,DE=DG,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴∠A=∠DCG=90°,
∴CD⊥CG;
(2)解:∵四边形DEFG是正方形,
∴EF=GF,∠EFM=∠GFM=45°,
在△EFM和△GFM中,
∴△EFM≌△GFM(SAS),
∴EM=GM,∠MEF=∠MGF,
在△EFH和△GFN中,,
∴△EFH≌△GFN(ASA),
∴HF=NF,
∵tan∠MEN==,
∴GF=EF=3HF=3NF,
∴GH=2HF,
作NP∥GF交EM于P,则△PMN∽△HMG,△PEN∽△HEF,
∴=,==,
∴PN=HF,
∴====;
(3)EM的长不可能为,
理由:假设EM的长为,
∵点E是AB边上一点,且∠EDG=∠ADC=90°,
∴点G在BC的延长线上,
同(2)的方法得,EM=GM=,
∴GM=,
在Rt△BEM中,EM是斜边,
∴BM<,
∵正方形ABCD的边长为1,
∴BC=1,
∴CM>,
∴CM>GM,
∴点G在正方形ABCD的边BC上,与“点G在BC的延长线上”相矛盾,
∴假设错误,
即:EM的长不可能为.
八、 列表法与树状图法(共5小题)
16. (2022•南充)为传播数学文化,激发学生学习兴趣,学校开展数学学科月活动,七年级开展了四个项目:A.阅读数学名著;B.讲述数学故事;C.制作数学模型;D.挑战数学游戏.要求七年级学生每人只能参加一项.为了解学生参加各项目情况,随机调查了部分学生,将调查结果制作成统计表和扇形统计图(如图),请根据图表信息解答下列问题:
项目
A
B
C
D
人数/人
5
15
a
b
(1)a= 20 ,b= 10 .
(2)扇形统计图中“B”项目所对应的扇形圆心角为 108 度.
(3)在月末的展示活动中,“C”项目中七(1)班有3人获得一等奖,七(2)班有2人获得一等奖,现从这5名学生中随机抽取2人代表七年级参加学校制作数学模型比赛,请用列表或画树状图法求抽中的2名学生来自不同班级的概率.
【解答】解:(1)被调查的总人数为5÷10%=50(人),
∴b=50×20%=10(人),
则a=50﹣(5+15+10)=20,
故答案为:20、10;
(2)扇形统计图中“B”项目所对应的扇形圆心角为360°×=108°,
故答案为:108;
(3)七(1)班3人分别用A、B、C表示,七(2)班2人分别D、E表示,
根据题意列表如下:
A
B
C
D
E
A
(B,A)
(C,A)
(D,A)
(E,A)
B
(A,B)
(C,B)
(D,B)
(E,B)
C
(A,C)
(B,C)
(D,C)
(E,C)
D
(A,D)
(B,D)
(C,D)
(E,D)
E
(A,E)
(B,E)
(C,E)
(D,E)
共有20种等可能的情况数,其中这两人来自不同班级的有12种,
则这两人来自不同班级的概率是=.
17. (2021•南充)某市体育中考自选项目有乒乓球、篮球和羽毛球,每个考生任选一项作为自选考试项目.
(1)求考生小红和小强自选项目相同的概率;
(2)除自选项目之外,长跑和掷实心球为必考项目.小红和小强的体育中考各项成绩(百分制)的统计图表如下:
考生
自选项目
长跑
掷实心球
小红
95
90
95
小强
90
95
95
①补全条形统计图.
②如果体育中考按自选项目占50%、长跑占30%、掷实心球占20%计算成绩(百分制),分别计算小红和小强的体育中考成绩.
【解答】解:(1)将乒乓球、篮球和羽毛球分别记作A、B、C,列表如下:
A
B
C
A
(A,A)
(B,A)
(C,A)
B
(A,B)
(B,B)
(C,B)
C
(A,C)
(B,C)
(C,C)
由表可知共有9种等可能结果,其中小红和小强自选项目相同的有3种结果,
所以小红和小强自选项目相同的概率为=;
(2)①补全条形统计图如下:
②小红的体育中考成绩为95×50%+90×30%+95×20%=93.5(分),
小强的体育中考成绩为90×50%+95×30%+95×20%=92.5(分).
18. (2019•南充)现有四张完全相同的不透明卡片,其正面分别写有数字﹣2,﹣1,0,2,把这四张卡片背面朝上洗匀后放在桌面上.
(1)随机地取一张卡片,求抽取的卡片上的数字为负数的概率.
(2)先随机抽取一张卡片,其上的数字作为点A的横坐标;然后放回并洗匀,再随机抽取一张卡片,其上的数字作为点A的纵坐标,试用画树状图或列表的方法求出点A在直线y=2x上的概率.
【解答】解:(1)随机的取一张卡片,抽取的卡片上的数字为负数的概率为P==;
(2)画树状图如图所示:
共有16个可能的结果,点A在直线y=2x上的结果有2个,
∴点A在直线y=2x上的概率为P==.
19. (2020•南充)今年,全球疫情大爆发,我国派遣医疗专家组对一些国家进行医疗援助.某批次派出20人组成的专家组,分别赴A、B、C、D四个国家开展援助工作,其人员分布情况如统计图(不完整)所示:
(1)计算赴B国女专家和D国男专家人数,并将条形统计图补充完整.
(2)根据需要,从赴A国的专家中,随机抽取两名专家对当地医疗团队进行培训,求所抽取的两名专家恰好是一男一女的概率.
【解答】解:(1)赴B国女专家人数为20×40%﹣5=3(人)
赴D国男专家人数为20×(1﹣20%﹣40%﹣25%)﹣2=1(人)
条形统计图补充为:
(2)画树状图为:
共有20种等可能的结果数,其中所抽取的两名专家恰好是一男一女的结果数为12,
所以所抽取的两名专家恰好是一男一女的概率==.
20. (2018•南充)“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分
7
8
9
10
人数/人
2
5
4
4
(1)这组数据的众数是 8 ,中位数是 9 .
(2)已知获得10分的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
【解答】解:(1)由于8分出现次数最多,
所以众数为8,
中位数为第8个数,即中位数为9,
故答案为:8、9;
(2)画树状图如下:
由树状图可知,共有12种等可能结果,其中恰好抽到八年级两名领操员的有2种结果,
所以恰好抽到八年级两名领操员的概率为=.
相关试卷
这是一份浙江省温州市五年(2018-2022)中考数学真题分类汇编-05 解答题中档题,共27页。试卷主要包含了图3中画出相应的格点图形.等内容,欢迎下载使用。
这是一份05解答题中档题-浙江台州市五年(2018-2022)中考数学真题分类汇编,共12页。试卷主要包含了解方程组等内容,欢迎下载使用。
这是一份05解答题中档题知识点分类-天津市五年(2018-2022)中考数学真题分类汇编,共14页。试卷主要包含了解不等式组,,绘制出如下的统计图①和图②等内容,欢迎下载使用。












