

最后一题考前押题+--2022年初中数学中考备考冲刺(含答案)
展开
这是一份最后一题考前押题+--2022年初中数学中考备考冲刺(含答案),共50页。试卷主要包含了抛物线经过和两点等内容,欢迎下载使用。
(1)求的值及,满足的关系式;
(2)抛物线同时经过两个不同的点和,求的值;
(3)若抛物线在和两点间随的增大而减少,求的取值范围.
2.如图,已知点P在矩形ABCD外,∠APB=90°,PA=PB,点E、F分别在AD、BC上运动,且∠EPF=45°,连接EF.
(1)求证:△APE∽△BFP;
(2)若△PEF是等腰直角三角形,求的值;
(3)试探究线段AE、BF、EF之间满足的等量关系,并证明你的结论.
3.科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽路空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系如图所示;小钢球离地面高度(米)与它的运动时间(秒)之间的函数关系如图中抛物线所示.
(1)直接写出与之间的函数关系式;
(2)求出与之间的函数关系式;
(3)小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?
4.如图,已知抛物线y=ax2+bx+c(a≠0) 的对称轴为x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求线段BC所在直线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出此点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
5.如图,⊙O的直径AB垂直于弦CD于点E,,,点P是CD延长线上异于点D的一个动点,连结AP交⊙O于点Q,连结CQ交AB于点F,则点F的位置随着点P位置的改变而改变.
(1)如图1,当时,求的值;
(2)如图2,连结AC,DQ,在点P运动过程中,设,.
①求证:;
②求y与x之间的函数关系式.
6.如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,﹣),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和的值.
(3)点F (0,y)是y轴上一动点,当y为何值时,FC+BF的值最小.并求出这个最小值.
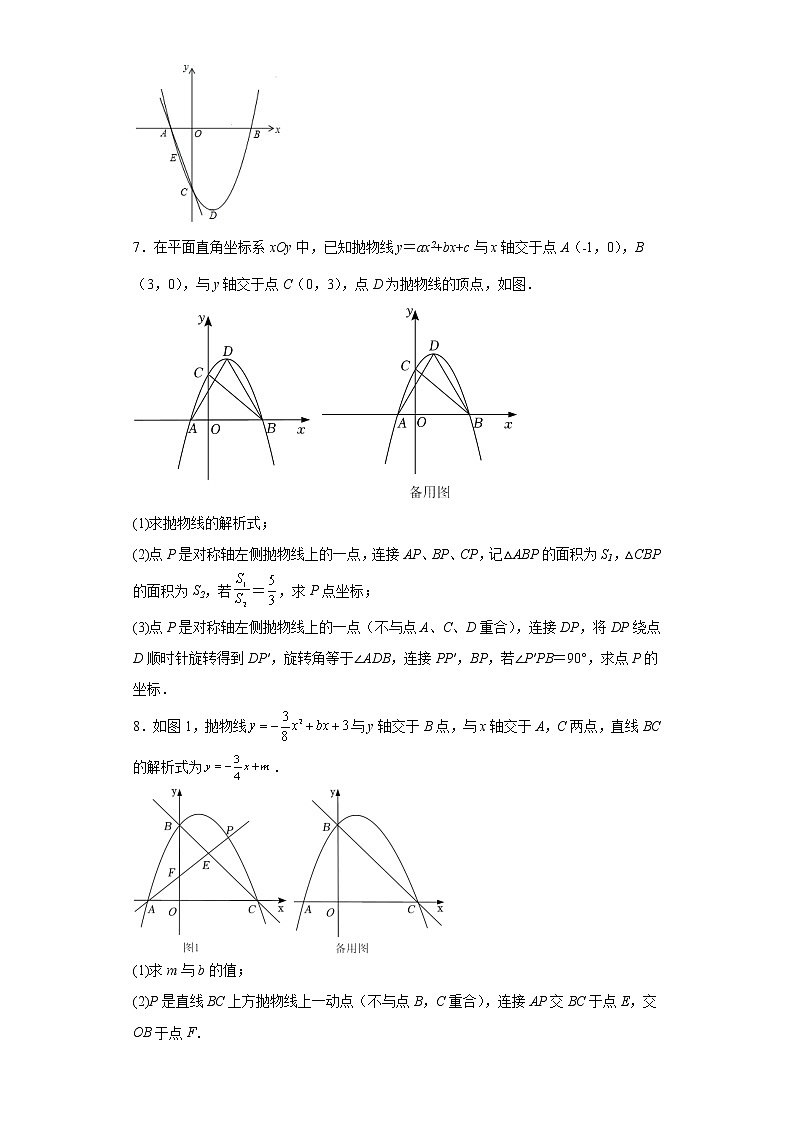
7.在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,3),点D为抛物线的顶点,如图.
(1)求抛物线的解析式;
(2)点P是对称轴左侧抛物线上的一点,连接AP、BP、CP,记△ABP的面积为S1,△CBP的面积为S2,若=,求P点坐标;
(3)点P是对称轴左侧抛物线上的一点(不与点A、C、D重合),连接DP,将DP绕点D顺时针旋转得到DP′,旋转角等于∠ADB,连接PP′,BP,若∠P′PB=90°,求点P的坐标.
8.如图1,抛物线与y轴交于B点,与x轴交于A,C两点,直线BC的解析式为.
(1)求m与b的值;
(2)P是直线BC上方抛物线上一动点(不与点B,C重合),连接AP交BC于点E,交OB于点F.
①是否存在最大值?若存在,求出的最大值.并直接写出此时点E的坐标;若不存在,说明理由.
②当△BEF为等腰三角形时,直接写出点P的坐标.
9.如图,抛物线y=ax2+x﹣4a与x轴交于A(﹣1,0),B两点,与y轴交于点C,在直线BC上方的抛物线上有一动点E,过点E作EG⊥x轴于G,EG交直线BC于点F,过点E作ED⊥BC于点D.
(1)求抛物线及直线BC的函数关系式;
(2)设S△EDF为S1,S△BGF为S2,当S1=S2时,求点E的坐标.
(3)在(2)的条件下,在y轴上是否存在点M,使得∠MAB=2∠EAB?若存在,请直接写出点M的坐标;若不存在,请说明理由.
10.在Rt△ABC中,∠ACB=90°,AC=9,sin∠BAC=·点D在边AB上(不与点A、B重合),以AD为半径的⊙A与射线AC相交于点E,射线DE与射线BC相交于点F,射线AF与⊙A交于点G,
(1)如图1,设AD=x,用含x的代数式表示DE的长;
(2)如果点E是的中点,求∠AFD的余切值;
(3)如果△AFD为等腰三角形,直接写出AD的长.
11.在中,弦平分圆周角,连接,过点作DE//AB交的延长线于点.
(1)求证:是的切线;
(2)若,且是的中点,的直径是,求的长.
(3)是弦下方圆上的一个动点,连接和,过点作于点,请探究点在运动的过程中,的比值是否改变,若改变,请说明理由;若不变,请直接写出比值.
12.如图所示,平面直角坐标系中,二次函数y=a(x+2k)(x﹣k)图象与x轴交于A、B两点,抛物线对称轴为直线x=﹣2;
(1)求k的值;
(2)点C为抛物线上一点,连接BC、AC,作CD⊥x轴于D,当∠BCA=90°时,设CD长度为d,求d与a的函数关系式;
(3)抛物线顶点为S,作ST垂直AB于T,点Q为第一象限抛物线上一点,连接AQ交ST于点P,过B作x轴的垂线交AQ延长线于点E,连接OE交BQ于点G,过O作OE的垂线交AQ于点F,若OF=OG,tan∠ABQ=2时,连接SQ,求证:SQ=SP.
13.如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接PC.
(1)求直线BC的解析式;
(2)抛物线对称轴与BC交于点D,点P为直线BC下方对称轴右侧抛物线上的一点,连接PB,PD.当△BDP的面积最大时,Q从点P出发,先沿适当的路径运动到y轴上的点M处,再沿适当的路径运动到抛物线对称轴上点N处,最后沿适当的路径运动到点B处停止.求点Q经过的最短路径的长;
(3)将△BOC绕点O顺时针旋转60°得到△B′OC′,点B,C的对应点分别为B′,C′,点E为直线BC上一点,连接B′E,C′E.当△B′C′E为等腰三角形时,求符合条件的点E的坐标.
14.已知,内接于,AO平分.
(1)如图1,求证:;
(2)如图2,点D是上一点,连接BD交AC于点G,连接CD,弦AE交BD于F、交CD于H,且,求证:;
(3)如图3,在(2)的条件下,BD经过圆心O,连接DE,,的面积为,求的半径.
15.如图,四边形ABCD是⊙O的内接矩形,过点A的切线与CD的延长线交于点M,连接OM与AD交于点E,AD>1,CD=1
(1)求证:△DBC∽△AMD;
(2)设AD=x,求△COM的面积(用x的式子表示);
(3)若∠AOE=∠COD,求OE的长.
16.如图,直线y=﹣x+3与x轴交于点A,与y轴交于点B,抛物线y=ax2+x+c经过A、B两点.
(1)求二次函数解析式;
(2)如图1,点E在线段AB上方的抛物线上运动(不与A、B重合),过点E作ED⊥AB,交AB于点D,作EF⊥AC,交AC于点F,交AB于点M,求△DEM的周长的最大值;
(3)在(2)的结论下,连接CM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、C、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
(4)如图2,点N的坐标是(1,0),将线段ON绕点O逆时针旋转得到ON′,旋转角为α(0°<α<90°),连接N′A、N′B,求N′A+N′B的最小值.
1.(1);
(2)
(3)a的取值范围为0<a≤1或-1≤a<0;
【解析】
(1)把点A和B代入抛物线的解析式,即可得出答案;
(2)先求解抛物线的对称轴为,再根据抛物线同时经过两个不同的点和,可得对称轴为 再建立方程求解即可;
(3)先求出抛物线的对称轴,根据图象的开口方向和二次函数的增减性即可得出答案.
(1)
解:∵抛物线y=ax2+bx+c经过点A(0,4)和B(2,0),
∴,
∴;
(2)
解:由(1)得:抛物线为:
该抛物线的对称轴为,
抛物线同时经过两个不同的点和,
该抛物线的对称轴为
解得: 经检验符合题意;∴b=-2a-2=-2×-12-2=1-2=-1.
(3)
由(1)可得:y=ax2+(-2a-2)x+4,
∴该抛物线的对称轴为,
∵抛物线在A、B两点间y随x的增大而减小,
∴当a>0时,开口向上,对称轴在B点右侧或经过B点, 即,
∵a>0, ∴a+1≥2a,
解得a≤1, ∴0<a≤1.
当a<0时,开口向下,对称轴在A点左侧或经过A点, 即,
∵a<0,
∴a+1≥0, 解得a≥-1,
∴-1≤a<0.
综上, a的取值范围为0<a≤1或-1≤a<0.
2.(1)见解析
(2)或2
(3)线段AE,BF,EF之间满足的等量关系是AE2+BF2=EF2.证明见解析
【解析】
(1)根据矩形的性质和相似三角形的判定得出△APE∽△BFP即可;
(2)根据相似三角形的性质得出比例关系,分两种情况进行讨论解答即可;
(3)利用全等三角形的判定和性质以及勾股定理解答即可.
(1)
∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°.
∵∠APB=90°,PA=PB,
∴∠PAB=∠PBA=45°.
∴∠PAE=∠PAB+∠BAD=45°+90°=135°,∠FBP=∠PBA+∠ABC=45°+90°=135°,
∴∠PAE=∠PBF.
∴∠APE+∠AEP=45°.
∵∠EPF=45°,∠APB=90°,
∴∠APE+∠BPF=45°.
∴∠AEP=∠BPF.
∴△APE∽△BFP.
(2)
∵△APE∽△BFP,
∴.
∵△PEF是等腰直角三角形,∠EPF=45°,
∴可分为两种情况讨论:
①当∠PEF=90°,PE=EF时,则.
∴.
∴,.
∵AP=BP,
∴.
②当∠PFE=90°,PF=EF时,则.
∴.
∴,.
∵AP=BP,
∴.
综上所述,的值为或2.
(3)
线段AE,BF,EF之间满足的等量关系是AE2+BF2=EF2.
证明:延长AB到G,使得BG=AE,连接PG,FG,
∵∠PBA=45°,
∴∠PBG=135°.
∵∠PAE=135°,
∴∠PBG=∠PAE.
∵PA=PB,BG=AE,
∴△PBG≌△PAE(SAS).
∴BG=AE,PG=PE,∠BPG=∠APE.
∵∠APE+∠BPF=∠EPF=45°,
∴∠BPG+∠BPF=∠EPF.
即∠GPF=∠EPF.
又∵PF=PF,PG=PE,
∴△PGF≌△PEF(SAS).
∴GF=EF.
∵∠ABC=90°,
∴∠GBF=90°.
∴由勾股定理得,BG2+BF2=GF2.
∴AE2+BF2=EF2.
3.(1);(2);(3)70米
【解析】
(1)先设出一次函数的解析式,再用待定系数法求函数解析式即可;
(2)用待定系数法求函数解析式即可;
(3)当1<x≤6时小钢球在无人机上方,因此求y2-y1,当6<x≤8时,无人机在小钢球的上方,因此求y1-y2,然后进行比较判断即可.
解:(1)设y1与x之间的函数关系式为y1=kx+b',
∵函数图象过点(0,30)和(1,35),
则,
解得,
∴y1与x之间的函数关系式为.
(2)∵时,,
∵的图象是过原点的抛物线,
∴设,
∴点,在抛物线上.
∴,即,
解得,
∴.
答:与的函数关系式为.
(3)设小钢球和无人机的高度差为米,
由得或.
①时,
,
∵,∴抛物线开口向下,
又∵,
∴当时,的最大值为;
②时,
,
∵,∴拋物线开口向上,
又∵对称轴是直线,
∴当时,随的增大而增大,
∵,
∴当时,的最大值为70.
∵,
∴高度差的最大值为70米.
答:高度差的最大值为70米.
4.(1)y=x+3
(2)M(-1,2)
(3)P点的坐标为(-1,-2)或(-1,4)或(-1,)或(-1,).
【解析】
(1)根据对称轴为x=-1,且抛物线经过A(1,0),C(0,3)两点,待定系数法求抛物线解析式即可,进而求得点的坐标,待定系数法求直线解析式即可,
(2)根据对称性求最值即可,设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小,
(3)设P(-1,t),又B(-3,0),C(0,3),①若点B为直角顶点,②若点C为直角顶点,③若点P为直角顶点,根据勾股定理求解即可.
(1)
)根据题意:,
解得,
∴抛物线的解析式为y=-x2-2x+3.
∵抛物线的对称轴为x=-1,且抛物线过点A(1,0),
∴把B(-3,0),C(0,3)分别代入y=mx+n得:
,
解得,
∴直线y=mx+n的解析式为y=x+3.
(2)
设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.
把x=-1代入y=x+3得:y=2.
∴M(-1,2),即当点M到点A的距离与到点C的距离之和最小时M的坐标为(-1,2).
(3)
设P(-1,t),又B(-3,0),C(0,3),
∴BC2=18,PB2=(-1+3)2+t2,PC2=(-1)2+(t-3)2=t2-6t+10.
①若点B为直角顶点,则BC2+PB2=PC2,即18+4+t2=t2-6t+10,解得t=-2;
②若点C为直角顶点,则BC2+PC2=PB2,即18+t2-6t+10=4+t2,解得t=4;
③若点P为直角顶点,则PB2+PC2=BC2,即4+t2+t2-6t+10=18,解得t1=,t2=.
综上所述,P点的坐标为(-1,-2)或(-1,4)或(-1,)或(-1,).
5.(1)
(2)①见解析 ②
【解析】
(1)根据垂径定理求出线段AE的长,由锐角三角形函数的定义可得出答案;
(2)①连接,由圆周角定理可得出答案;②由相似三角形的性质可得到和 的面积关系,再结合和的关系,即可得出答案.
(1)
解:连接,
直径,
.
,.
,
;
(2)
①证明:连接,
,
,
为直径,
,
,
,
;
②在中,AE=9,CE=3,
,
,,
,
,
,
,
.
6.(1)y=x2﹣x﹣2;(2)点E(﹣,﹣),=;(3)﹣,.
【解析】
(1)将点C、D的坐标代入抛物线表达式,即可求解;
(2)当△AOC∽△AEB时,=()2=()2=,求出yE=﹣,由△AOC∽△AEB得:==,即可求解;
(3)如图2,连接BF,过点F作FG⊥AC于G,当折线段BFG与BE重合时,取得最小值,即可求解.
解:(1)由题可列方程组:,
解得:
∴抛物线解析式为:y=x2﹣x﹣2;
(2)∵抛物线y=x2﹣x﹣2的图象与x轴交于A、B两点,
∴点A(﹣1,0),点B(3,0),
∴AO=1,BO=3,
∴∠AOC=90°,AC=,AB=4,
设直线AC的解析式为:y=kx+b,
则,
解得:,
∴直线AC的解析式为:y=﹣2x﹣2;
当△AOC∽△AEB时
∴=()2=()2=,
∵S△AOC=1,
∴S△AEB=,
∴AB×|yE|=,AB=4,则yE=﹣,
则点E(﹣,﹣);
由△AOC∽△AEB得:==,
∴=;
(3)如图2,连接BF,过点F作FG⊥AC于G,
则FG=CFsin∠FCG=CF,
∴CF+BF=GF+BF≥BE,
当折线段BFG与BE重合时,取得最小值,
由(2)可知∠ABE=∠ACO
∴BE=ABcs∠ABE=ABcs∠ACO=4×=,
|y|=OBtan∠ABE=OBtan∠ACO=3×=,
∴当y=﹣时,即点F(0,﹣),CF+BF有最小值为.
7.(1)
(2)
(3)
【解析】
(1)将点代入即可求解;
(2)过点作轴交于点,交于点,求出直线的解析式,设,则,利用三角形的面积公式求出的值,再根据建立方程,求出的值,由此即可得;
(3)过点作轴交于,过点作轴交于点,交于点,设,由旋转的性质可得,等量代换得到,即可证明,由,可得即,则,求出,即可求点坐标.
(1)
解:抛物线与轴交于点,
,
将点代入得:,
解得,
则.
(2)
解:如图1,过点作轴交于点,交于点,
设直线的解析式为,
将点代入得:,解得,
则直线的解析式为,
,
,
设,则,
,
,
,
,
,
解得或(舍去)或(舍去),
则,
所以点的坐标为.
(3)
解:如图2,过点作轴交于,过点作轴交于点,交于点,
设,
绕点顺时针旋转得到,
,
∵旋转角等于,
,
,点是抛物线的顶点,
,
,
,
,
,
,
,
,
,
,即,
,
,
,
,
,
,
解得或(舍去)或(舍去)或(舍去),
则,
所以点的坐标为.
8.(1),;
(2)①存在最大值,的最大值为,此时E点的坐标为(1,);②P点坐标为(,)或(2,3)或(,)
【解析】
(1)先求抛物线与y轴交点B(0,3),然后利用待定系数法求一出函数解析式,求出点C坐标,然后把点C坐标代入抛物线解析式即可;
(2)①存在最大值,理由如下:过点P作PG∥x轴交BC于点G,先求A(﹣2,0),C(4,0),设P(n,),且0<n<4,可求G点的纵坐标为,求出PG=n﹣()=,利用相似三角形△PEG∽△AEC,可得,可得当n=2时,的最大值为,然后利用待定系数求直线AP的解析式为,联立方程组,求出点E坐标即可;②过点E作EM⊥y轴于点M,设P(p,),且0<p<4,利用待定系数法求直线AP的解析式为,求出F(0,),再联立方程组,求出E,根据勾股定理得,BE2=BM2+EM2=,EF2=MF2+EM2=,若△BEF为等腰三角形,则分以下三种情况:(Ⅰ)当BE=BF时,则BE2=BF2,即,(Ⅱ)当BE=EF时,则BE2=EF2,即=,(Ⅲ)当BF=EF时,则BF2=EF2,即=,解方程即可
(1)
解:∵抛物线与y轴交于B点,
当x=0时,y=3,
∴B(0,3),
∵直线BC的解析式为y=﹣x+m,
∴m=3,
即直线BC的解析式为y=﹣x+3,
当y=0时,﹣x+3=0,
解得x=4,
∴C(4,0),
把C点坐标代入二次函数解析式得﹣×42+b×4+3=0,
解得b=;
(2)
①存在最大值,理由如下:
过点P作PG∥x轴交BC于点G,
由(1)得,抛物线的解析式为,
当y=0时,,
解得x=﹣2或4,
∴A(﹣2,0),C(4,0),
∴OA=2,OC=4,AC=6,
∵P是直线BC上方抛物线上的动点(不与点B,点C重合),
设P(n,),且0<n<4,
∴G点的纵坐标为,
又∵G点在直线BC上,
∴G(,),
∴PG=n﹣()=,
∵PG∥x轴,
∴△PEG∽△AEC,
∴,
∵,
∴,
即当n=2时,的最大值为,
此时P(2,3),
设直线AP的解析式为y=kx+t,
代入A点和P点的坐标得,
解得,
∴直线AP的解析式为,
联立方程组,
解得,
∴E(1,),
即存在最大值,的最大值为,此时E点的坐标为(1,);
②过点E作EM⊥y轴于点M,
则∠BME=∠FME=90°,
∵P是直线BC上方抛物线上的一点(不与点B,点C重合),
设P(p,),且0<p<4,
设直线AP的解析式为y=sx+h,
把A(﹣2,0),P(p,)代入解析式得,
,
解得,
∴直线AP的解析式为,
令x=0时, ,
∴F(0,),
∴OF=,
∵B(0,3),
∴OB=3,
∴BF=3﹣,
联立方程组,
解得,
∴E,
∵EM⊥y轴,
∴EM=,OM=,
∴MF=OM﹣OF=,BM=OB﹣OM=3﹣,
在Rt△MBE和Rt△FME中,根据勾股定理得,
BE2=BM2+EM2=,EF2=MF2+EM2=,
若△BEF为等腰三角形,则分以下三种情况:
(Ⅰ)当BE=BF时,则BE2=BF2,
即,
解得p=或p=(不符合题意,舍去),
此时P(,);
(Ⅱ)当BE=EF时,则BE2=EF2,
即=,,
解得p=2,(经检验符合题)
此时P(2,3);
(Ⅲ)当BF=EF时,则BF2=EF2,
即=,
解得p=,(经检验符合题意)
此时P(,);
综上,符合条件的P点坐标为(,)或(2,3)或(,)
9.(1)y=﹣x2+x+3,y=﹣x+3
(2)E(3,3)
(3)存在,点M的坐标为(0,)或(0,﹣)
【解析】
(1)利用待定系数法求出两个函数解析式;
(2)设E(m,-m2+m+3),则F(m,-m+3),用m表示出EF,证明△BGF∽△EDF,得到,求得5ED=9BG,利用三角函数得cs∠DEF=cs∠OBC,求出4EF=9BG,列得4(-m2+3m)=9(4﹣m),求出m即可得到点E的坐标;
(3)①当点M在y轴的正半轴上时, 过点E作EP⊥AM于P,过点E作EN⊥x轴于点N,过点P作QH∥x轴,交NE于H,过点A作AQ⊥PH于Q,由三角函数得到tan∠EAN=tan∠PAE=, 证明△EHP∽△PQA,得到,设EH=3x,PQ=4x,则PH=4﹣4x,AQ=3+3x,求出x得到点P的坐标,由此求出直线AP的解析式即可得到点M;②当点M在y轴的负半轴上时,同理得:M(0,-).
(1)
把A(﹣1,0)代入抛物线y=ax2+x﹣4a中得:a﹣﹣4a=0,
∴a=﹣,
∴抛物线的解析式为:y=-x2+x+3,
当y=0时,-x2+x+3=0,
解得:x1=﹣1,x2=4,
∴B(4,0),
当x=0时,y=3,
∴C(0,3),
设直线BC的解析式为:y=kx+b,
则,解得:,
∴直线BC的解析式为:y=-x+3;
(2)
如图1,设E(m,-m2+m+3),则F(m,-m+3),
∴EF=(-m2+m+3)-(-m+3)=-m2+3m,
∵ED⊥BC,EG⊥AB,
∴∠EDF=∠BGF=90°,
∵∠DFE=∠BFG,
∴△BGF∽△EDF,
∴,
∵S1=S2,
∴,
∴,
∴5ED=9BG,
∵∠DEF=∠OBC,
∴cs∠DEF=cs∠OBC,
∴,
∴DE=EF,
∴4EF=9BG,
∴4(-m2+3m)=9(4﹣m),
解得:m1=3,m2=4(舍),
∴E(3,3);
(3)
分两种情况:
①当点M在y轴的正半轴上时,如图2,
过点E作EP⊥AM于P,过点E作EN⊥x轴于点N,过点P作QH∥x轴,交NE于H,过点A作AQ⊥PH于Q,
∵∠MAB=2∠EAB,
∴∠PAE=∠EAB,
∴PE=EN=3,
tan∠EAN=tan∠PAE=,
∵∠H=∠Q=90°,∠HPE=∠QAP,
∴△EHP∽△PQA,
∴,
设EH=3x,PQ=4x,则PH=4﹣4x,AQ=3+3x,
∴,
∴x=,
∴P(,),
∴AP的解析式为:y=x+,
∴M(0,);
②当点M在y轴的负半轴上时,同理得:M(0,-),
综上,点M的坐标为(0,)或(0,-).
10.(1)
(2)
(3)或或
【解析】
(1)过点D作DH⊥AC,垂足为H.根据锐角三角函数和勾股定理即可用x的代数式表示DE的长;
(2)根据题意可设BC=4k(k>0),AB=5k,则AC=3k.过点A作AM⊥DE,垂足为M,再根据锐角三角函数和勾股定理即可表示∠DFA的余切值;
(3)分三种情况讨论:①当时,②时,③时,根据(1)(2)的结论解直角三角形即可.
(1)
如图,过点D作DH⊥AC,垂足为H.
在Rt△ADH中,DH=AD•sin∠BAC=x,
AH==.
在⊙A中,AE=AD=x,
∴EH=AE−AD=x−=,
∴DE==;
(2)
∵sin∠BAC=,
∴可设BC=4k(k>0),AB=5k,
则AC==3k.
∵AC=9,
∴3k=9,
∴k=3.
∴BC=12,AB=15.
∵点E是的中点,由题意可知此时点E在边AC上,点F在BC的延长线上,
∴∠FAC=∠BAC.
∵∠FCA=∠BCA=90°,AC=AC,
∴△FCA≌△BCA(ASA),
∴FC=BC=12.
∵∠AED=,
又∵∠AED=∠FEC,且∠AED、∠FEC都为锐角,
∴tan∠FEC=2.
∴EC=
∴AE=AC−EC=9−6=3.
过点A作AM⊥DE,垂足为M,
则EM=ED=.
∵sin∠AED=,
∴AM=AE•sin∠AED=.
在Rt△EFC中,EF=.
∴在Rt△AFM中,ct∠AFD=.
答:∠DFA的余切值为;
(3)
①当时,点E在AC上
,tan∠FEC= tan∠AED=2,
∵FC=CE•tan∠FEC=2(9−x),
,
DE=,
,
中,
,
解得,
,
②当时,
即,
解得,
,
③当时,,C三点重合,此时,
综上所述,的长为或或.
11.(1)见解析
(2)
(3)不变;
【解析】
(1)根据圆周角定理先说明,即可得出,根据等腰三角形的性质得出,即可证得结论;
(2)构建直角三角形,利用勾股定理求出线段长度即可求解;
(3)利用相似三角形,直角三角形,找到角之间的关系,然后转化为线段的关系进行求解.
(1)
证明:如图,连接交于点,连接,,,
平分,
,
,
,
,
,
,
,
是的切线.
(2)
如图,连接,,,OB,过点作于点,如图所示:
,
,,
,
设,,
的直径是,
,
,
,
解得:,
,,
,
是的中点,
,
,
,
,
,
.
(3)
如图,延长至使得,连接,,连接,,连接交于点,连接,
,,,四点共圆,
,
,
,
,
是的切线,
,
,
,
是的中点,
,
,
,
,,,四点共圆,
,
,,
,
,
,
,
,
,,
,
.
12.(1)k=4
(2)
(3)见解析
【解析】
(1)根据抛物线y=a(x+2k)(x-k)与x轴交于A、B两点,可得A(-2k,0),B(k,0),利用对称轴x=-2即可求出k;
(2)先证明△CAD∽△BCD,可得CD2=AD•BD,设C(x,y),则D(x,0),AD=x-(-8)=x+8,BD=4-x,d=CD=y=a(x+8)(x-4),建立方程求解即可;
(3)过点F作FM⊥AB于点M,过点G作GN⊥AB于点N,过点Q作QH⊥AB于点H,设Q(t,a(t+8)(t-4)),则BH=4-t,QH=a(t+8)(t-4),根据tan∠ABQ=2,可求得即可得运用待定系数法分别求出直线AQ、直线OE、直线BQ的解析式,联立直线OE与直线BQ的解析式,可求得点G的坐标,再证明△OFM≌△GON,即可得点F的坐标,将F坐标代入直线AQ解析式即可求得a的值,将a的值代入计算即可证得结论.
(1)
∵抛物线y=a(x+2k)(x﹣k)与x轴交于A、B两点,
∴A(﹣2k,0),B(k,0),
∵对称轴为直线x=﹣2,
∴=﹣2,
∴k=4;
(2)
如图1,设C(x,y),则D(x,0),
由(1)知,k=4,y=a(x+8)(x﹣4),
∴A(﹣8,0),B(4,0),
∴AD=x﹣(﹣8)=x+8,BD=4﹣x,d=CD=y=a(x+8)(x﹣4),
∵CD⊥x轴于D,∠BCA=90°,
∴∠ADC=∠CDB=90°,
∵∠ACD+∠BCD=∠ACD+∠CAD=90°,
∴∠CAD=∠BCD,
∴△CAD∽△BCD,
∴=,
∴CD2=AD•BD,
∴[a(x+8)(x﹣4)]2=(x+8)(4﹣x),
∴(x+8)(x﹣4)[a2(x+8)(x﹣4)+1]=0,
∵点C不与A、B重合,
∴(x+8)(x﹣4)≠0,
∴a2(x+8)(x﹣4)+1=0,
∴(x+8)(x﹣4)=﹣,
∴d=a(x+8)(x﹣4)=a×(﹣)=﹣,
∴d与a的函数关系式为:d=﹣;
(3)
如图2,过点F作FM⊥AB于点M,过点G作GN⊥AB于点N,过点Q作QH⊥AB于点H,
设Q(t,a(t+8)(t﹣4)),则BH=4﹣t,QH=a(t+8)(t﹣4),
∵tan∠ABQ=2,
∴=2,即QH=2BH,
∴a(t+8)(t﹣4)=2(4﹣t),
∴(t﹣4)(at+8a+2)=0,
∴t=4(舍去)或t=﹣,
∴Q(﹣,),
设直线AQ解析式为y=k1x+b1,将A(﹣8,0),Q(﹣,)分别代入,
得:,
解得:,
∴直线AQ解析式为y=(﹣12a﹣2)x﹣96a﹣16,
∴P(﹣2,﹣72a﹣12),E(4,﹣144a﹣24),
设直线OE解析式为y=mx,则4m=﹣144a﹣24,
∴m=﹣36a﹣6,
∴直线OE解析式为y=(﹣36a﹣6)x,
设直线BQ解析式为y=k2x+b2,
∴,
解得:,
∴直线BQ解析式为y=﹣2x+8,
联立直线OE与直线BQ的解析式,得,
解得:,
∴G(﹣,),
∵OE⊥OF,FM⊥AB,GN⊥AB,
∴∠EOF=∠OMF=∠ONG=90°,
∵∠FOM+∠GON=∠FOM+∠OFM=90°,
∴∠OFM=∠GON,
∵OF=OG,
∴△OFM≌△GON(AAS),
∴OM=GN=,FM=ON=﹣,
∴F(﹣,﹣),
∵点F在直线AQ上,
∴(﹣12a﹣2)×(﹣)﹣96a﹣16=﹣,
解得:a=﹣,
∴抛物线解析式为y=﹣(x+8)(x﹣4)=﹣(x+2)2+,
∴S(﹣2,),
∵直线AQ解析式为
∴P(﹣2,3),
∴,
∵,
∴
∴SQ=SP.
13.(1)y=x﹣3
(2)
(3)点E的坐标为(,)或(,)或(,)或(,)
【解析】
(1)先求出抛物线与x轴和y轴的交点坐标,再用勾股定理的逆定理判断出△ABC是直角三角形;
(2)先求出S△PBD最大时,P(,﹣),然后判断出所走的路径最短,即最短路径的长为PM+MN+NB的长,计算即可;
(3)△A′C1E′是等腰三角形,分三种情况分别建立方程计算即可.
(1)
解:∵抛物线y=x2﹣x﹣3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,
当x=0时,y=﹣3,
当y=0时,
x2﹣x﹣3=0,
解得:x1=﹣,x2=3,
∴A(﹣,0),B(3,0),C(0,﹣3),
设直线BC解析式为y=kx+b,将B(3,0),C(0,﹣3)代入,
得,
解得:,
∴直线BC解析式为y=x﹣3;
(2)
解:如图1,过点P作PG∥y轴,
由(1)知:直线BC解析式为y=x﹣3,B(3,0),
设P(a,a2﹣a﹣3),
∴G(a,a﹣3),
∴PG=a﹣3﹣(a2﹣a﹣3)=﹣a2+a,
∵y=x2﹣x﹣3=(x﹣)2﹣4,
∴抛物线对称轴为x=,
∴点D的横坐标为,
S△PBD=×(3﹣)×PG=(﹣a2+a)=﹣(a﹣)2+,
∵0<a<3,﹣<0,
∴当a=时,S△PBD最大,此时点P(,﹣),
如图2,作点P关于y轴的对称点P′(﹣,﹣),连接P′B,交y轴于点M,交抛物线对称轴于点N,
连接PM,点Q沿P→M→N→B运动,M所走的路径最短,即最短路径的长为PM+MN+NB的长,
∵P、P′关于y轴对称,
∴PM=P′M,
∴PM+MN+NB=P′M+MN+NB=P′B,
作P′H⊥x轴于点H,P′B=,
∴点Q经过的最短路径的长为PM+MN+AN=;
(3)
解:如图3,过C′作C′R⊥x轴于点R,作B′T⊥y轴于点T,
设E(m,m﹣3),
∵将△BOC绕点O顺时针旋转60°得到△B'OC',
∴∠COC′=∠BOB′=60°,OC′=OC=3,OB′=OB=3,
∴∠C′OR=∠B′OT=30°,
∵∠ORC′=∠OTB′=90°,
∴C′R=,OR=,B′T=,OT=,
∴C′(﹣,﹣),B′(,﹣),
∴B′C′2=BC2=OB2+OC2=(3)2+32=36,
C′E2=[m﹣(﹣)2+[m﹣3﹣(﹣)]2=m2+2m+9,
B′E2=(m﹣)2+[m﹣3﹣(﹣)]2=m2﹣2m+9,
∵△B'C'E为等腰三角形,
∴B′C′=C′E或B′C′=B′E或C′E=B′E,
当B′C′=C′E时,36=m2+2m+9,
解得:m=,
∴E(,)或(,);
当B′C′=B′E时,36=m2﹣2m+9,
解得:m=,
∴E(,)或(,),
当C′E=B′E时,m2+2m+9=m2﹣2m+9,
解得:m=0,
当m=0时,点B′,C′,E三点在一条直线上,不能构成三角形.
综上所述,点E的坐标为(,)或(,)或(,)或(,).
14.(1)见解析
(2)见解析,
(3)4+8
【解析】
(1)连接OB,OC,根据同圆半径相等,利用等腰三角形两底角相等和角平分线定义,证得∠OBA=∠OCA,∠OBC=∠OCB,所以∠OBA+∠OBC=∠OAC+∠OCB,即可得出结论;
(2)连接AD,过点A作,交CD延长线于M,证△ADM≌△ADF(AAS),得AM=AF,DM=DF,再证Rt△AMC≌△AFB(HL),得CM=BF,即可得出结论;
(3)连接AD, OE,设∠ABO=∠OAB=∠OAC=∠ACD =α,因为,所以∠CAE=∠ACD=α,∠AED=∠CDE,由于F,所以∠ABO+∠OAB+∠OAC+∠CAE=90°,即4α=90°,所2α=45°,从而可证得△DFH是等腰直角三角形,△OAF是等腰直角三角形,得到, EH=DH=DF,OA=OF,再由S△DEH=,求得DF=4,由OF+DF=OD=OA,即OF+4=OF,求得OF=4+4,最后由OD=OF+DF求得答案.
(1)
解:如图1,连接OB,OC,
∵OA=OB,
∴∠OAB=∠OBA,
∵OA=OC,
∴∠OAC=∠OCA,
∵AO平分,
∴∠OAB=∠OAB,
∴∠OBA=∠OCA,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBA+∠OBC=∠OAC+∠OCB
即∠ABC=∠ACB;
(2)
证明:如图2,连接AD,过点A作,交CD延长线于M,
∵四边形ABCD内接于⊙O,
∴∠ADM=∠ABC,
由(1)知,∠ACB=∠ABC,
∴AB=AC,
∴∠ADM=∠ACB,
∵∠ACB=∠ADB,
∴∠ADM=∠ADB,
∵于M,于F,
∴∠AMD=∠AFD=90°,
在△ADM和△ADF中,
∴△ADM≌△ADF(AAS),
∴AM=AF,DM=DF,
在Rt△AMC和Rt△AFB中,
,
∴Rt△AMC≌Rt△AFB(HL),
∴CM=BF,
∴CD+DM=BF,
∴BD+CD=BF+DF+CD=BF+DM+CD=2BF;
(3)
解:如图3,连接AD,OH,OE,
设∠ABO=∠OAB=∠OAC=∠ACD =α,
∵,
∴∠CAE=∠ACD=α,∠AED=∠CDE,
∴DH=EH,
∵于F,
∴∠ABO+∠OAB+∠OAC+∠CAE=90°,
即4α=90°,
∴2α=45°,
∴∠BDC=∠BAC=2α=45°,
∴∠FDH=∠DHF=2α=45°,
∴△DFH是等腰直角三角形,
∴EH=DH=DF,
∵S△DEH=,
∴,
∴DF=4,
∵∠OAF=∠OAC+∠CAF=2α=45°,
∴△OAF是等腰直角三角形,
∴OA=OF,
∴OF+DF=OD=OA,
∴OF+4=OF,
∴OF=4+4,
∴OD=OF+DF=4+4+4=4+8,
答:⊙O的半径为4+8.
15.(1)见解析
(2)
(3)
【解析】
(1)证明∠MAD=∠BAC=∠BDC,从而得证;
(2)证明△ADC∽△MAD,得出DM,从而求出CM,再根据三角形的中位线求出CM上的高,从而解得;
(3)延长OB交MA的延长线于G,证明AM=AG,计算表示出AM和AG,从而得出方程,求出x的值,进而解得OE.
(1)
∵AM是⊙O的切线,
∴OA⊥AM,
∴∠CAM=90°,
∴∠MAD+∠DAC=90°,
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=∠ADC=90°,
∴∠BAC+∠DAC=90°,
∴∠MAD=∠BAC,
对于:
∠BAC=∠BDC,
∴∠MAD=∠BDC,
又∠MDA=∠BCD=90°,
∴△DBC∽△AMD;
(2)
如图2,
取CD的中点N,连接ON,
∵四边形ABCD是矩形,
∴AO=CO,
∴ON∥AD,ON,
∴∠CNO=∠ADC=90°,
∴ON⊥CM,
由(1)知:△DBC∽△AMD,
∴DM
∴CM=DM+CD=x2+1,
∴S△COMCM•ON(x2+1)•
(3)
如图3,
作DF⊥AC于F,延长DB交MA的延长线于G
在Rt△ADC中,AD=x,CD=1,
∴AC,
∴OD=OCAC
DF,
CF
∴OF=OC﹣CF,
∵DF∥AG,
∴△DOF∽△GOA,
∴AG
∴AG2
为直径
又
AM2=DM•MC=x2(x2+1),
∵∠AOE=∠COD,
∠AOG=∠COD,
∴∠AOE=∠AOG,
∵OA=OA,
∠OAM=∠OAG,
∴△AOM≌△AOG(ASA),
∴AG=AM,
∴x2(x2+1),
∴x1,x2(舍去),
∴AD,OD,DF=,OF,
作EH⊥OA于H,设OE=a,
∴EH=OE•sin∠AOE=a•sin∠DOF=a
∴OHa,
由AH+OH=OA得,
∴a,
即OE.
16.(1)
(2)的周长的最大值为
(3)存在,或或
(4)
【解析】
(1)、由一次函数与坐标轴交点坐标特点求出A、B两点坐标,代入二次函数解析式即可求解;
(2)、设 ,则可用m表示出点M、F点坐标,由两点间的坐标公式,可用m表示出周长,再证明 ,则由周长比等于相似比,即可表示出周长,将得到的式子配成顶点式并利用二次函数性质即可求解;
(3)、由(2)可知E、M点坐标,则可分成AM为边和AM为对角线去求解即可;
(4)、在y轴上截取OH= ,连接 ,可证得:,则可得当H、 、A共线时,有最小值,且最小值为 ,再由勾股定理即可求解.
(1)
解:∵直线y=﹣x+3与x轴交于点A,与y轴交于点B,
∴令x=0,则y=3;
令y=0,则x=4,
,
∵抛物线y=ax2+x+c经过A、B两点,
,
解得: ,
;
(2)
设,则 , ,
, ,
,
∵点E在线段AB上方的抛物线上运动(不与A、B重合),
,
,
的周长为: ,
∵ED⊥AB, EF⊥AC,
,
,
,
的周长∶的周长=
,
,
的周长为:,
,
,
时,的周长最大值为 ;
(3)
存在点P,
由(2)可知: ,
此时可得: ,
,
∴抛物线的对称轴为: ,
则Q点的横坐标为1,
,
,
设 ,
①当CM为平行四边形的边时,且P点在Q点的左侧,
此时: ,
C点先向右平移4个单位,再向上平移个单位到M,
则P点先向右平移4个单位,再向上平移个单位到Q,
∵Q点的横坐标为1,
∴ ,
将其代入抛物线解析式得: ,
,
②当CM为平行四边形的边时,且P点在Q点的右侧,
同理可知:将Q点先向右平移4个单位,再向上平移个单位到P,
此时 ,
代入抛物线解析式得: ,
,
③当CM为平行四边形对角线时,由中点坐标公式得:
,
,
代入抛物线解析式得: ,
综上所述:或或;
(4)
在y轴上截取OH= ,连接 ,
,
,
,
又 ,
,
,
,
,
当H、 、A共线时,有最小值,且最小值为 ,
在直角三角形AOH中, ,
∴的最小值为 .
相关试卷
这是一份解答题考前押题+--2022年初中数学中考备考冲刺(含答案),共27页。试卷主要包含了通过实验研究发现,已知关于的一元二次方程等内容,欢迎下载使用。
这是一份基础知识选择题考前押题+--2022年初中数学中考备考冲刺(含答案),共15页。试卷主要包含了下列四个数中,是负数的是,下列说法中,正确的是,化简的结果是,已知,则代数式的值为,是下列哪个方程的解,方程组的解是的解是等内容,欢迎下载使用。
这是一份基础知识填空题考前押题+--2022年初中数学中考备考冲刺(含答案),共18页。试卷主要包含了已知等内容,欢迎下载使用。










