2021学年5.6 函数 y=Asin（ ωx ＋ φ）第一课时导学案

这是一份2021学年5.6 函数 y=Asin（ ωx ＋ φ）第一课时导学案，共9页。

知识点 A，ω，φ对y＝A sin (ωx＋φ)图象的影响
1．φ对函数y＝sin (x＋φ)，x∈R图象的影响
2．ω(ω＞0)对y＝sin (ωx＋φ)图象的影响
3．A(A＞0)对y＝A sin (ωx＋φ)图象的影响
[研读]A影响y轴方向上的伸缩，ω影响周期，φ影响x轴方向上的平移．
eq \a\vs4\al(【思辨】) 判断正误(请在括号中打“√”或“×”).
(1)由函数y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4))) 的图象得到y＝sin x的图象，必须向左平移 eq \f(π,4) 个单位长度．( × )
(2)把函数y＝sin x的图象上所有点的横坐标伸长到原来的3倍就得到函数y＝sin 3x的图象．( × )
(3)利用图象变换作图时，“先平移，后伸缩”与“先伸缩，后平移”中平移的长度是一致的．( × )
(4)函数y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4))) 的图象向右平移 eq \f(π,4) 个单位长度后所得图象与函数y＝－cs x重合．( √ )
【解析】 (1)由函数y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4))) 的图象得到y＝sin x的图象，可以向右平移 eq \f(π,4) 个单位长度．
(2)把函数y＝sin x的图象上所有点的横坐标伸长到原来的3倍就得到函数y＝sin eq \f(1,3) x的图象．
(3)利用图象变换作图时，“先平移，后伸缩”与“先伸缩，后平移”中平移的长度不一定是一致的．当ω＝1时，是一致的，当ω≠1时，是不一致的．
(4)函数y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4))) 的图象向右平移 eq \f(π,4) 个单位长度后所得图象对应的函数是y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,2))) .因为y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,2))) ＝－cs x，所以此说法正确．
eq \(\s\up7(),\s\d5( “五点法”作图))
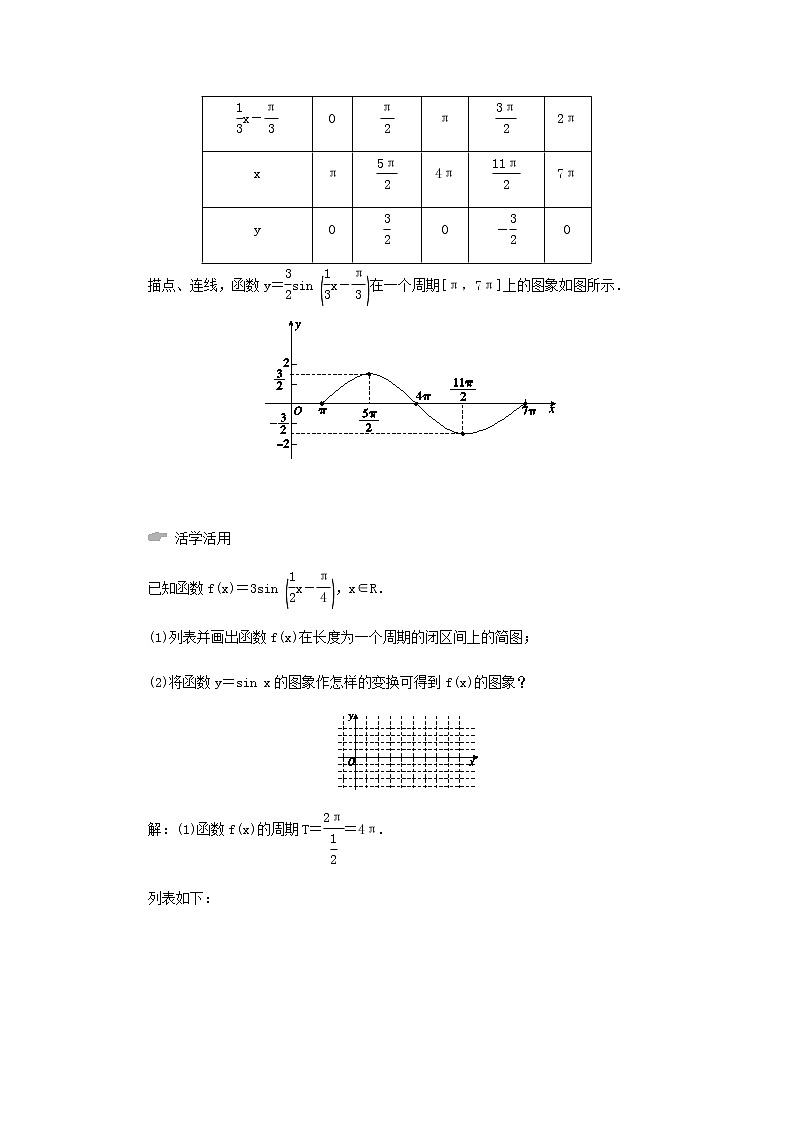
eq \a\vs4\al(例1) 用“五点法”作出函数y＝ eq \f(3,2) sin eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)x－\f(π,3))) 在一个周期上的简图．
解：函数y＝ eq \f(3,2) sin eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)x－\f(π,3))) 的周期T＝6π.列表：
描点、连线，函数y＝ eq \f(3,2) sin eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)x－\f(π,3))) 在一个周期[π，7π]上的图象如图所示．
活学活用
已知函数f(x)＝3sin eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x－\f(π,4))) ，x∈R．
(1)列表并画出函数f(x)在长度为一个周期的闭区间上的简图；
(2)将函数y＝sin x的图象作怎样的变换可得到f(x)的图象？
解：(1)函数f(x)的周期T＝ eq \f(2π,\f(1,2)) ＝4π.
列表如下：
描点、连线，得到一个周期的简图．图象如下：
(2)先把y＝sin x的图象向右平移 eq \f(π,4) 个单位长度，然后把所有点的横坐标伸长为原来的2倍(纵坐标不变)，再把所有点的纵坐标扩大为原来的3倍(横坐标不变)，得到f(x)的图象．
[规律方法]
用“五点法”作函数f(x)＝A sin (ωx＋φ)图象的步骤．
第一步：列表：
第二步：在同一坐标系中描出各点；
第三步：用光滑曲线连接这些点，形成图象．
eq \(\s\up7(),\s\d5( f（x）＝A sin （ωx＋φ）图象的平移变换))
eq \a\vs4\al(例2) 函数y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(3x－\f(π,2))) 的图象是由y＝sin 3x的图象经过怎样的变换得到的？
解：y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(3x－\f(π,2))) ＝sin eq \b\lc\[\rc\](\a\vs4\al\c1(3\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6))))) ，所以y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(3x－\f(π,2))) 的图象可以看作是把y＝sin 3x图象上所有点向右平移 eq \f(π,6) 个单位长度得到的．
活学活用
若要得到y＝cs eq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,5))) 的图象，只要将y＝sin 2x的图象( C )
A．向左平移 eq \f(π,10) 个单位长度
B．向右平移 eq \f(π,10) 个单位长度
C．向左平移 eq \f(7π,20) 个单位长度
D．向右平移 eq \f(7π,20) 个单位长度
【解析】 y＝sin 2x＝cs eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,2))) ＝cs eq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4))))) ，又y＝cs eq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,5))) ＝cs eq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,10))))) ，所以将y＝sin 2x的图象上所有点向左平移 eq \f(7π,20) 个单位长度，即可得到函数y＝cs eq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,5))) 的图象．
[规律方法]
(1)已知两函数解析式，判断其图象间的平移关系时，要将异名三角函数化为同名三角函数；
(2)若x的系数不为1，应提取系数确定平移的单位和方向，方向遵循左加右减．
eq \(\s\up7(),\s\d5( f（x）＝A sin （ωx＋φ）图象的伸缩变换))
eq \a\vs4\al(例3) 将函数y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3))) 的图象上所有点的横坐标缩短到原来的 eq \f(1,2) (纵坐标不变)而得到的函数解析式为__y＝sin__ eq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3))) __．
【解析】 将函数y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3))) 的图象上所有点的横坐标缩短到原来的 eq \f(1,2) ，则周期变为原来的 eq \f(1,2) ，所以得到的函数解析式为y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3))) .
活学活用
为了得到函数g(x)＝cs eq \b\lc\(\rc\)(\a\vs4\al\c1(3x－\f(π,3))) 的图象，只需将函数f(x)＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6))) 图象上所有点的( A )
A．横坐标缩短到原来的 eq \f(2,3)
B．横坐标伸长到原来的 eq \f(3,2) 倍
C．横坐标缩短到原来的 eq \f(2,3) ，再向右平移 eq \f(π,12) 个单位长度
D．横坐标伸长到原来的 eq \f(3,2) 倍，再向右平移 eq \f(π,12) 个单位长度
【解析】 由题可得f(x)＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6))) ＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,2)－\f(π,3))) ＝cs eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3))) ，故只需将其图象上所有点的横坐标缩短到原来的 eq \f(2,3) ，即可得到函数g(x)＝cs eq \b\lc\(\rc\)(\a\vs4\al\c1(3x－\f(π,3))) 的图象，故选A.
【迁移探究】说明y＝2sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) ＋1的图象是由y＝sin x 的图象经过怎样变换得到的．
解：方法一(先伸缩后平移)：将y＝sin x的图象上所有点的横坐标缩短到原来的 eq \f(1,2) (纵坐标不变)，得到y＝sin 2x的图象；将y＝sin 2x的图象向右平移 eq \f(π,12) 个单位长度，得到y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) 的图象；将y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) 的图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)，得到y＝2sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) 的图象；再将y＝2sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) 的图象向上平移1个单位长度，得到函数y＝2sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) ＋1的图象．
方法二(先平移后伸缩)：将y＝sin x的图象向右平移 eq \f(π,6) 个单位长度，得到y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6))) 的图象；将y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6))) 的图象上所有点的横坐标缩短到原来的 eq \f(1,2) (纵坐标不变)，得到y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) 的图象；将y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) 的图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)，得到y＝2sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) 的图象；再将y＝2sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) 的图象向上平移1个单位长度，得到函数y＝2sin eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) ＋1的图象．
[规律方法]
由函数y＝sin x的图象通过变换得到函数y＝A sin (ωx＋φ)(A>0，ω>0)的图象的步骤：
1．将函数y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3))) 的图象向左平移 eq \f(π,3) 个单位长度，得到的图象对应的函数是( D )
A．y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(2π,3)))
B．y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(2π,3)))
C．y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6)))
D．y＝sin x
【解析】 将函数y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3))) 的图象向左平移 eq \f(π,3) 个单位长度，得到的图象对应的函数是y＝sin x．
2．将函数y＝sin x的图象上所有点的纵坐标缩短到原来的 eq \f(2,3) (横坐标不变)，则所得图象对应的函数为( B )
A．y＝ eq \f(3,2) sin x
B．y＝ eq \f(2,3) sin x
C．y＝sin eq \f(3,2) x
D．y＝sin eq \f(2,3) x
【解析】 将函数y＝sin x的图象上所有点的纵坐标缩短到原来的 eq \f(2,3) ，横坐标不变，则所得图象对应的函数是y＝ eq \f(2,3) sin x．
3．已知函数f(x)＝cs eq \b\lc\(\rc\)(\a\vs4\al\c1(ωx－\f(π,6))) (ω＞0)的相邻两个零点的距离为 eq \f(π,2) ，要得到y＝f(x)的图象，只需把y＝cs ωx的图象( A )
A．向右平移 eq \f(π,12) 个单位
B．向左平移 eq \f(π,12) 个单位
C．向右平移 eq \f(π,6) 个单位
D．向左平移 eq \f(π,6) 个单位
【解析】 由已知得 eq \f(2π,ω) ＝2× eq \f(π,2) ，故ω＝2，y＝cs 2x向右平移 eq \f(π,12) 个单位可得y＝cs eq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,12))))) ＝cs eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) 的图象．
4．将函数y＝sin x的图象上所有点的横坐标缩短到原来的 eq \f(1,4) (纵坐标不变)，得到__y＝sin__4x__的图象．
【解析】 将函数y＝sin x的图象上所有点的横坐标缩短到原来的 eq \f(1,4) (纵坐标不变)，得到y＝sin 4x的图象．
5．将函数y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(3x＋\f(π,4))) 的图象向右平移 eq \f(π,8) 个单位长度，再将图象上各点的横坐标扩大到原来的3倍(纵坐标不变)，则所得的图象对应的函数解析式是__y＝sin__ eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,8))) __．
【解析】 y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(3x＋\f(π,4))) 的图象向右平移 eq \f(π,8) 个单位长度得到y＝sin eq \b\lc\[\rc\](\a\vs4\al\c1(3\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,8)))＋\f(π,4))) ＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(3x－\f(π,8))) 的图象，再将y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(3x－\f(π,8))) 的图象上各点的横坐标扩大到原来的3倍(纵坐标不变)得到y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,8))) 的图象，故所得的图象对应的函数解析式是y＝sin eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,8))) .
eq \a\vs4\al(温馨说明：课后请完成高效作业48 ) eq \f(1,3) x－ eq \f(π,3)
0
eq \f(π,2)
π
eq \f(3π,2)
2π
x
π
eq \f(5π,2)
4π
eq \f(11π,2)
7π
y
0
eq \f(3,2)
0
－ eq \f(3,2)
0
eq \f(1,2) x－ eq \f(π,4)
0
eq \f(π,2)
π
eq \f(3π,2)
2π
x
eq \f(π,2)
eq \f(3π,2)
eq \f(5π,2)
eq \f(7π,2)
eq \f(9π,2)
3sin eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x－\f(π,4)))
0
3
0
－3
0
ωx＋φ
0
eq \f(π,2)
π
eq \f(3π,2)
2π
x
－ eq \f(φ,ω)
eq \f(π,2ω) － eq \f(φ,ω)
eq \f(π,ω) － eq \f(φ,ω)
eq \f(3π,2ω) － eq \f(φ,ω)
eq \f(2π,ω) － eq \f(φ,ω)
f(x)
0
A
0
－A
0