苏教版 (2019)必修 第二册13.2 基本图形位置关系第1课时达标测试

第1课时　直线与平面平行的判定

【概念认知】

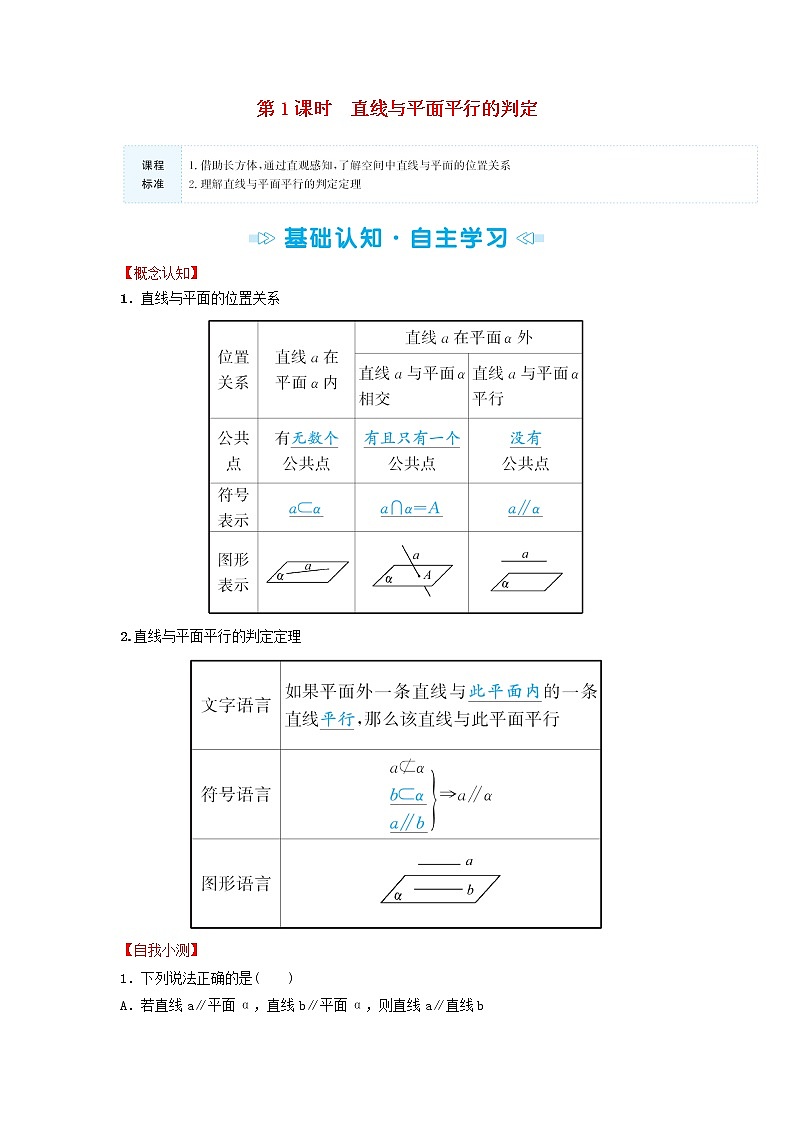
1．直线与平面的位置关系

2.直线与平面平行的判定定理

【自我小测】

1．下列说法正确的是(　　)

A．若直线a∥平面α，直线b∥平面α，则直线a∥直线b

B．若直线a∥平面α，直线a与直线b相交，则直线b与平面α相交

C．若直线a∥平面α，直线a∥直线b，则直线b∥平面α

D．若直线a∥平面α，则直线a与平面α内任意一条直线都无公共点

【解析】选D.A中直线a与直线b也可能异面、相交，所以不正确；B中，直线b也可能与平面α平行，所以不正确；C中，直线b也可能在平面α内，所以不正确；根据直线与平面平行的定义知D正确．

2．若直线l与平面α不平行，则下列结论正确的是________．(填序号)

①α内的所有直线都与直线l异面；

②α内不存在与l平行的直线；

③α内的直线与l相交；

④直线l与平面α有公共点．

【解析】①中，过公共点的直线与直线l相交，不异面，①错误；②③中，当l⊂α时，α内有无数条直线与l平行，故②③错；④中，直线l与平面α不平行，则直线l与平面α相交或在平面内，所以l与平面α有公共点，故④正确．

答案：④

3．若平面外一条直线上有两点到该平面的距离相等，则这条直线与平面的位置关系是________．

【解析】当两点在平面的一侧时，这条直线与平面平行；当两点在平面的两侧时，这条直线与平面相交．所以这条直线与平面的位置关系是平行或相交．

答案：平行或相交

4．正方体ABCD­A1B1C1D1中，E为DD1的中点，则BD1与过A，C，E三点的平面的位置关系是________．

【解析】如图所示，连接BD交AC于点O.在正方体中容易得到点O为BD的中点．

又因为E为DD1的中点，所以OE∥BD1.又因为OE⊂平面ACE，BD1⊄平面ACE，所以BD1∥平面ACE.

答案：平行

5．长方体ABCD­A1B1C1D1中E为AA1的中点，F为BB1的中点，与EF平行的长方体的面有________个．

【解析】如图，因为EF∥A1B1，EF⊄平面A1B1C1D1，A1B1⊂平面A1B1C1D1，所以EF∥平面A1B1C1D1.同理EF∥平面ABCD，EF∥平面DD1C1C.

答案：3

6．如图，正方形ABCD与正方形ABEF所在平面相交于AB，在AE，BD上各取一点P，Q，且AP＝DQ.求证：PQ∥平面BCE.

【证明】如图所示， 在平面ABEF内过P作PM∥AB交BE于点M，在平面ABCD内过点Q作QN∥AB交BC于点N，连接MN.

因为PM∥AB，所以＝.

又因为QN∥AB∥CD，所以＝，

即＝.

因为正方形ABEF与ABCD有公共边AB，

所以AE＝DB.

因为AP＝DQ，所以PE＝BQ，

所以PM＝QN.

又因为PM∥AB，QN∥AB，

所以PM∥QN.

所以四边形PQNM为平行四边形．

所以PQ∥MN.

又因为MN⊂平面BCE，PQ⊄平面BCE.

所以PQ∥平面BCE.

【基础全面练】

一、单选题

1．M∈l，N∈l，N∉α，M∈α，则有(　　)

A．l∥α    B．l⊂α

C．l与α相交    D．以上都有可能

【解析】选C.由符号语言知，直线l上有一点在平面α内，另一点在α外，故l与α相交．

2．下列说法正确的个数为(　　)

①若直线l上有无数个点不在平面α内，则l∥α；

②如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行；

③若直线l与平面α平行，则l与平面α内的任意一条直线都没有公共点．

A．0　    B．1　    C．2　    D．3

【解析】选B.如图所示：借助长方体模型，棱AA1所在直线上有无数个点在平面ABCD外，但棱AA1所在直线与平面ABCD相交，所以①不正确．

A1B1∥AB，A1B1所在直线平行于平面ABCD，但直线AB⊂平面ABCD，所以②不正确．

直线l与平面α平行，则l与α无公共点，l与平面α内所有直线都没有公共点，所以③正确．

3．下列给出的四个命题，正确的个数是(　　)

(1)若直线与平面不相交，则直线与平面平行．

(2)过一点有且只有一条直线与已知直线平行．

(3)直线l上有无数多个点在平面α外，则l∥α.

(4)过平面外一点有且只有一条直线与该平面平行．

A．0　    B．1　    C．2　     D．4

【解析】选A.(1)错误，若直线与平面不相交，则直线在平面内或直线与平面平行．

(2)错误，当点在已知直线上时，不存在过该点的直线与已知直线平行，故(2)错．

(3)错误，直线l也可能与平面α相交．

(4)错误，在棱柱的上底面内，过一点任意作一条直线都与棱柱的下底面平行，所以过平面外一点与已知平面平行的直线有无数条，故(4)错．

二、多选题

4．下列四个正方体图形中，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，能得到AB∥平面MNP的图形是(　　)

【解析】选AD.过AB的体对角面与平面MNP平行，故A成立；D中易知AB∥NP，故D也成立．

5．如图，一块矩形木板ABCD的一边AB在平面α内，把这块矩形木板绕AB转动，在转动的过程中，AB的对边CD与平面α的位置关系是(　　)

A.平行    B．相交

C．在平面α内    D．以上都有可能

【解析】选AC.在旋转过程中，CD∥AB，易得CD∥α或CD⊂α.

三、填空题

6．能保证直线a与平面α平行的条件是________(填序号).

(1)b⊂α，a∥b；

(2)b⊂α，c∥α，a∥b，a∥c；

(3)b⊂α，A，B∈a，C，D∈b，且AC∥BD；

(4)a⊄α，b⊂α，a∥b.

【解析】由直线与平面平行的判定定理可知(4)正确．

答案：(4)

7．如图，在五面体ABCDEF中，四边形CDEF为矩形，M，N分别是BF，BC的中点，则MN与平面ADE的位置关系是________．(填“平行”或“相交”)

【解析】因为M，N分别是BF，BC的中点，

所以MN∥CF.又因为四边形CDEF为矩形，所以CF∥DE，所以MN∥DE.又因为MN⊄平面ADE，DE⊂平面ADE，所以MN∥平面ADE.

答案：平行

四、解答题

8．直三棱柱ABC­A1B1C1中，D是AB的中点．证明：BC1∥平面A1CD.

【证明】如图，连接AC1交A1C于点F，则F为AC1的中点．

又D是AB的中点，连接DF，则BC1∥DF.

因为DF⊂平面A1CD，BC1⊄平面A1CD，所以BC1∥平面A1CD.

9．如图，在三棱台DEFABC中，AB＝2DE，G，H分别为AC，BC的中点．求证：BD∥平面FGH.

【证明】在三棱台DEFABC中，AB＝2DE，G为AC的中点，可得DF∥GC，DF＝GC，

所以四边形DFCG为平行四边形，连接CD，FG.

设CD∩FG＝O，则O为CD的中点．

又H为BC的中点，所以OH∥BD.

又OH⊂平面FGH，BD⊄平面FGH，

所以BD∥平面FGH.

【综合突破练】

一、选择题

1．如图所示，已知正方体ABCD­A1B1C1D1中，E，F分别是它们所在线段的中点，则满足A1F∥平面BD1E的图形为(　　)

A．①    B．①②    C．②    D．①②③

【解析】选C.①中，平移A1F至D1F′，知D1F′与平面BD1E只有一个交点D1，则A1F与平面BD1E不平行；

②中，在正方体ABCDA1B1C1D1中，E，F分别是它们所在线段的中点，则易知A1F∥D1E，而A1F⊄平面BD1E，D1E⊂平面BD1E，故A1F∥平面BD1E；

③中，同①平移A1F至D1F′，知D1F′与平面BD1E只有一个交点D1，则A1F与平面BD1E不平行；

2．已知在棱长均为2的正三棱柱ABCA1B1C1中，点D为B1C1的中点，若在棱AB上存在一点P，使得B1P∥平面ACD，则B1P的长度为(　　)

A．2    B．    C．    D．3

【解析】选B.如图，设点P为AB的中点，取A1B1的中点Q，连接AQ，DQ，

则B1P∥AQ，又B1P⊄平面AQD，AQ⊂平面AQD，所以B1P∥平面AQD，

易知AC∥DQ，故平面AQD与平面ACD是同一个平面，

所以B1P∥平面ACD，此时B1P＝.

3．(多选)如图所示，P为矩形ABCD所在平面外一点，矩形对角线交点为O，M为PB的中点，下列结论正确的是(　　)

A.OM∥PD    B．OM∥平面PCD

C．OM∥平面PDA    D．OM∥平面PBA

【解析】选ABC.对于A，由于O为BD的中点，M为PB的中点，则OM∥PD，故正确；

对于B，由于OM∥PD，OM⊄平面PCD，PD⊂平面PCD，则OM∥平面PCD，故正确；

对于C，由于OM∥PD，OM⊄平面PAD，PD⊂平面PAD，则OM∥平面PAD，故正确；

对于D，由于M∈平面PAB，故错误．

二、填空题

4．下列说法中正确的个数是________.

①平行于同一平面的两直线平行；

②若直线a平行于平面α内的一条直线b，则直线a∥平面α；

③若两平行直线中的一条与平面α相交，则另一条也与平面α相交；

④若直线a与平面α内的无数条直线相交，则直线a在平面α内．

【解析】①②④错误，③正确．

答案：1

5．在梯形ABCD中，AB∥CD，AB⊂，CD⊄α，则CD与平面α内的直线的位置关系只能是________.

【解析】由条件知CD∥α，故CD与α内的直线平行或异面．

答案：平行或异面

6．P是△ABC所在平面外一点，E，F，G分别是AB，BC，PC的中点，则图中与过E，F，G的截面平行的线段有________条．

【解析】由题意知EF∥AC，FG∥PB，

所以AC∥平面EFG，PB∥平面EFG，即有2条与平面EFG平行的线段．

答案：2

7．在四面体A­BCD中，M，N分别是△ACD，△BCD的重心，则四面体的四个面中与MN平行的是______________．

【解析】连接AM并延长交CD于E，连接BN并延长交CD于F，由重心性质可知，E，F重合为一点，且该点为CD的中点，由＝得MN∥AB，因此，MN∥平面ABC且MN∥平面ABD.

答案：平面ABC，平面ABD

三、解答题

8．如图，空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点．

求证：(1)EH∥平面BCD；

(2)BD∥平面EFGH.

【证明】(1)因为EH为△ABD的中位线，所以EH∥BD.

因为EH⊄平面BCD，BD⊂平面BCD，

所以EH∥平面BCD.

(2)因为BD∥EH，BD⊄平面EFGH，EH⊂平面EFGH，

所以BD∥平面EFGH.

9．如图所示，已知A1B1C1­ABC是正三棱柱，D是AC的中点．求证：AB1∥平面DBC1.

【证明】因为A1B1C1­ABC是正三棱柱，

所以四边形B1BCC1是矩形．

连接B1C交BC1于点E，则B1E＝EC.

连接DE，在△AB1C中，

因为AD＝DC，B1E＝EC，所以DE∥AB1.

又因为AB1⊄平面DBC1，DE⊂平面DBC1，

所以AB1∥平面DBC1.