专题强化 一次（正比例）函数、方程和不等式综合性问题高分必刷题八年级数学下册《考点•题型•技巧》精讲与精练高分突破（人教版）

这是一份专题强化 一次（正比例）函数、方程和不等式综合性问题高分必刷题八年级数学下册《考点•题型•技巧》精讲与精练高分突破（人教版），共40页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．（2022·浙江杭州·八年级期末）设函数（为常数且）的图象过点．（ ）
A．若，则B．若，则
C．若，则D．若，则
2．（2022·重庆南开中学八年级期末）如图，在平面直角坐标系中，直线分别交x轴，y轴于A、B两点，C为线段OB上一点，过点C作轴交l于点D，若的顶点E恰好落在直线上，则点C的坐标为（ ）
A．B．C．D．
3．（2022·江苏无锡·八年级期末）如图，已知直线y＝ax+2与直线y＝mx+b的交点的横坐标是﹣2．根据图象有下列四个结论：①a＞0；②b＜0；③方程ax+2＝mx+b的解是x＝﹣2；④不等式ax﹣b＞mx﹣2的解集是x＞﹣2．其中正确的结论个数是（ ）
A．1B．2C．3D．4
4．（2022·广东揭阳·八年级期末）如图，直线y＝x，点A1坐标为（1，0），过点A1作x轴的垂线交直线于点B1，以原点O为圆心，OB1长为半径画弧x轴于点A2；再过点A2作x轴的垂线交直线于点B2，以原点O为圆心，OB2长为半径画弧交x轴于点A3，……，按此做法进行下去，点An的横坐标为（ ）
A．B．C．2D．2
5．（2022·安徽六安·八年级期末）函数y＝－3x＋1图象上有两点A（1，y₁），B（3，y₂），则y₁与y₂的大小关系是（ ）
A．y₁＞y₂B．y₁＜y₂C．y₁＝y₂D．无法确定
6．（2022·重庆实验外国语学校八年级阶段练习）、B两地相距320千米，甲、乙两车从地出发前往B地，甲车比乙车早小时出发，但比乙车晚小时到达B地，乙车出发一段时间后接到紧急通知需尽早到达B地，司机立即提速前往．甲车和乙车提速前后均保持匀速行驶，两车行驶路程（千米）与行驶时间（小时）之间的函数关系如图所示．则下列说法不正确的是（ ）
A．甲车的行驶速度为B．乙车到达B地时，甲车离B地还有
C．甲车行驶过程中有4个时刻与乙车相距D．乙车提速之后的速度为
7．（2022·甘肃兰州·八年级期末）正比例函数与一次函数在同一平面直角坐标系中的图象可能是（ ）
A．B．C．D．
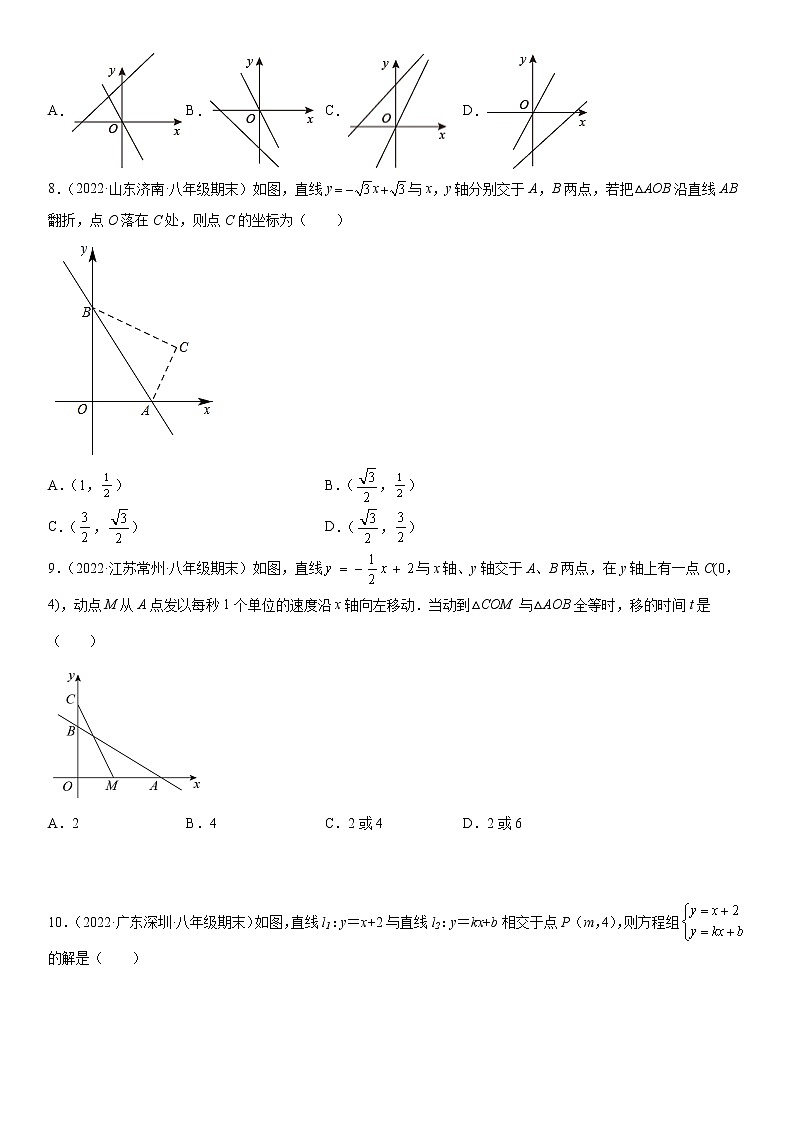
8．（2022·山东济南·八年级期末）如图，直线yx与x，y轴分别交于A，B两点，若把△AOB沿直线AB翻折，点O落在C处，则点C的坐标为（ ）
A．（1，）B．（，）
C．（，）D．（，）
9．（2022·江苏常州·八年级期末）如图，直线与x轴、y轴交于A、B两点，在y轴上有一点C(0，4)，动点M从A点发以每秒1个单位的速度沿x轴向左移动．当动到△COM 与△AOB全等时，移的时间t是（ ）
A．2B．4C．2或4D．2或6
10．（2022·广东深圳·八年级期末）如图，直线l1：y＝x+2与直线l2：y＝kx+b相交于点P（m，4），则方程组的解是（ ）
A．B．C．D．
11．（2022·广东佛山·八年级期末）如图，直线y＝kx+b（k≠0）与x轴交于点（﹣5，0），下列说法正确的是（ ）
A．k＞0，b＜0B．直线y＝bx+k经过第四象限
C．关于x的方程kx+b＝0的解为x＝﹣5D．若（x1，y1），（x2，y2）是直线y＝kx+b上的两点，若x1＜x2，则y1＞y2
12．（2022·山东济南·八年级期末）定义，图象与x轴有两个交点的函数y＝叫做关于直线x＝m的对称函数，它与x轴负半轴交点记为A，与x轴正半轴交点记为B例如：如图：直线l：x＝1，关于直线l的对称函数y＝与该直线l交于点C，当直线y＝x与关于直线x＝m的对称函数有两个交点时，则m的取值范围是（ ）
A．0≤m≤B．－2＜m≤C．－2＜m≤2D．－4＜m＜0
二、填空题
13．（2022·江苏连云港·八年级期末）我们知道函数的图象由无数个点组成，函数图象的平移本质上就是图象上点的平移．比如把直线向下平移3个单位，则直线经过点．若将直线向左平移2个单位，所得的直线对应的函数表达式为 __．
14．（2022·安徽蚌埠·八年级期末）数形结合是解决数学问题常用的思想方法．如图，直线与直线相交于点．根据图象可知，关于的不等式的解集是______
15．（2022·浙江杭州·八年级期末）设一次函数．若当时，；当时，，则的取值范围是______
16．（2022·江苏镇江·八年级期末）在平面直角坐标系中，一次函数，，均为常数）与正比例函数的图象如图所示，则关于的不等式的解集为__．
17．（2022·重庆·西南大学附中八年级期末）如图，已知直线交x轴于点B，交y轴于点A，点C在y轴负半轴上，，则直线BC的解析式为______．
18．（2022·四川成都·八年级期末）正方形A1B1C1O，A2B2C2C1，A3BC3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y＝kx+b（k＞0）和y轴上，已知点B1（1，1），B2（2，3），则点B3的坐标是 _____，点Bn的坐标是 _____．
19．（2022·辽宁沈阳·八年级期末）如图，△OAB1，△B1A1B2，△B2A2B3，…，△BnAnBn+1都是面积为的等边三角形，边AO在y轴上，点B1，B2，B3，…，Bn，Bn+1都在直线y＝x上，点A1，A2，A3，．．．，An都在直线y＝x的上方，观察图形的构成规律，用你发现的规律直接写出点A2022的坐标为_____．
三、解答题
20．（2021·四川眉山·八年级期中）某网店销售甲、乙两种羽毛球，已知甲种羽毛球每筒的售价比乙种羽毛球多15元，王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球，共花费255元．
（1）该网店甲、乙两种羽毛球每筒的售价各是多少元？
（2）根据消费者需求，该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒，且甲种羽毛球的数量大于乙种羽毛球数量的，已知甲种羽毛球每筒的进价为50元，乙种羽毛球每筒的进价为40元．
①若设购进甲种羽毛球m筒，则该网店有哪几种进货方案？
②若所购进羽毛球均可全部售出，请求出网店所获利润W（元）与甲种羽毛球进货量m（筒）之间的函数关系式，并说明当m为何值时所获利润最大？最大利润是多少？
21．（2020·江西抚州·八年级期末）如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A在x轴上，AB＝AC，∠BAC＝90°，且A（2，0）、B（3，3），BC交y轴于M，
（1）求点C的坐标；
（2）连接AM，求△AMB的面积；
（3）在x轴上有一动点P，当PB+PM的值最小时，求此时P的坐标．
22．（2021·广东揭阳·八年级期中）已知函数y=（m+1）x2-|m|+n+4．
（1）当m，n为何值时，此函数是一次函数？
（2）当m，n为何值时，此函数是正比例函数？
23．（2020·广东·深圳市福田区外国语学校八年级期中）如图，在平面直角坐标系中，直线l1：y=x与直线l2交点A的横坐标为2，将直线l1沿y轴向下平移4个单位长度，得到直线l3，直线l3与y轴交于点B，与直线l2交于点C，点C的纵坐标为﹣2．直线l2与y轴交于点D．
（1）求直线l2的解析式；
（2）求△BDC的面积．
24．（2021·广东肇庆·八年级期末）如图，直线l1的函数解析式为y=﹣2x+4，且l1与x轴交于点D，直线l2经过点A、B，直线l1、l2交于点C．
（1）求直线l2的函数解析式；
（2）求△ADC的面积；
（3）在直线l2上是否存在点P，使得△ADP面积是△ADC面积的2倍？如果存在，请求出P坐标；如果不存在，请说明理由．
25．（2020·安徽·合肥一六八中学八年级期中）某农产品生产基地收获红薯192吨，准备运给甲、乙两地的承包商进行包销．该基地用大、小两种货车共18辆恰好能一次性运完这批红薯，已知这两种货车的载重量分别为14吨/辆和8吨/辆，运往甲、乙两地的运费如下表：
（1）求这两种货车各用多少辆；
（2）如果安排10辆货车前往甲地，其余货车前往乙地，其中前往甲地的大货车为a辆，总运费为w元，求w关于a的函数关系式；
（3）在（2）的条件下，若甲地的承包商包销的红薯不少于96吨，请你设计出使总运费最低的货车调配方案，并求出最低总运费．
26．（2021·江苏·苏州高新区第一初级中学校八年级阶段练习）如图，直线与轴、轴分别交于两点，于点，点为直线上不与点重合的一个动点.
(1)求线段的长；
(2)当的面积是6时，求点的坐标；
(3)在轴上是否存在点，使得以、、为顶点的三角形与全等，若存在，请直接写出所有符合条件的点的坐标，否则，说明理由.
27．（2022·福建省华安县第一中学八年级阶段练习）如图，把矩形OABC放入平面直角坐标系xO中，使OA、OC分别落在x、y轴的正半轴上，其中AB＝15，对角线AC所在直线解析式为y＝﹣x+b，将矩形OABC沿着BE折叠，使点A落在边OC上的点D处．
（1）求点B的坐标；
（2）求EA的长度；
（3）点P是y轴上一动点，是否存在点P使得△PBE的周长最小，若存在，请求出点P的坐标，若不存在，请说明理由．
28．（2021·全国·八年级专题练习）如图，在平面直角坐标系xOy中，直线y＝－x＋与y＝x相交于点A，与x轴交于点B．
（1）求点A，B的坐标；
（2）在平面直角坐标系xOy中，是否存在一点C，使得以O，A，B，C为顶点的四边形是平行四边形？如果存在，试求出所有符合条件的点C的坐标；如果不存在，请说明理由；
（3）在直线OA上，是否存在一点D，使得△DOB是等腰三角形？如果存在，试求出所有符合条件的点D的坐标，如果不存在，请说明理由．
29．（2019·湖北襄阳·八年级期末）如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（﹣3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H，连接BM.
（1）菱形ABCO的边长 ；
（2）求直线AC的解析式；
（3）动点P从点A出发，沿折线ABC方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，
①当0＜t＜时，求S与t之间的函数关系式；
②在点P运动过程中，当S=3，请直接写出t的值．
30．（2022·四川·成都新津为明学校八年级期中）如图，直线l1：y1=﹣x+2与x轴，y轴分别交于A，B两点，点P（m，3）为直线l1上一点，另一直线l2：y2=x+b过点P．
（1）求点P坐标和b的值；
（2）若点C是直线l2与x轴的交点，动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒．
①请写出当点Q在运动过程中，△APQ的面积S与t的函数关系式；
②求出t为多少时，△APQ的面积小于3；
③是否存在t的值，使△APQ为等腰三角形？若存在，请求出t的值；若不存在，请说明理由．
车型
运费
运往甲地/（元/辆）
运往乙地/（元/辆）
大货车
720
800
小货车
500
650
参考答案：
1．A
【解析】
【分析】
将点代入函数（为常数且），得，根据不等式的性质即可得出答案．
【详解】
A选项，若，则，即，故A正确，符合题意；
B选项，若，则，即，故本选项不符合题意；
C选项，若，即，则，故本选项不符合题意；
D选项，若，，则，不符合题意．
故选：A．
【点睛】
本题考查了一次函数上点的坐标特征，解答本题的关键是明确题意，找出所求问题需要的条件，利用不等式的性质解答．
2．D
【解析】
【分析】
设点 ，根据轴，可得点 ，再根据平行四边形的性质可得点轴， ，则， ，即可求解．
【详解】
解：设点 ，
∵轴，
∴点 ，
∵四边形是平行四边形，
∴轴， ，
∴点 ，
∴ ，
∵直线分别交y轴于B两点，
∴当 时， ，
∴点 ，
∴ ，
∴，解得： ，
∴ ，
∴点 ．
故选：D
【点睛】
本题主要考查了一次函数的图形和性质，平行四边形的性质，熟练掌握一次函数的图形和性质，平行四边形的性质，利用数形结合思想解答是解题的关键．
3．D
【解析】
【分析】
根据图象得：直线y＝ax+2的图像自左向右逐渐上升，直线y＝mx+b交y轴于负半轴，从而得到a＞0，b＜0，故①②正确；再由直线y＝ax+2与直线y＝mx+b的交点的横坐标是﹣2．可得方程ax+2＝mx+b的解是x＝﹣2，故③正确；然后观察图象可得当x＞﹣2时，直线y＝ax+2的图象位于直线y＝mx+b的图象得上方，可得不等式ax+2＞mx+b的解集为x＞﹣2，故④正确，即可求解．
【详解】
解：根据图象得：直线y＝ax+2的图像自左向右逐渐上升，直线y＝mx+b交y轴于负半轴，
∴a＞0，b＜0，故①②正确；
∵直线y＝ax+2与直线y＝mx+b的交点的横坐标是﹣2．
∴当x＝﹣2时，ax+2＝mx+b，
∴方程ax+2＝mx+b的解是x＝﹣2，故③正确；
∵ax﹣b＞mx﹣2，
∴ax+2＞mx+b，
∵当x＞﹣2时，直线y＝ax+2的图象位于直线y＝mx+b的图象得上方，
∴不等式ax+2＞mx+b的解集为x＞﹣2，
即不等式ax﹣b＞mx﹣2的解集是x＞﹣2．故④正确
∴正确的结论为①②③④，共有4个．
故选：D
【点睛】
本题主要考查了一次函数的交点问题，熟练掌握一次函数的图象和性质是解题的关键．
4．A
【解析】
【分析】
先根据一次函数方程式求出点的坐标，在根据点的坐标求出点的坐标，以此类推总结规律便可求出点的横坐标．
【详解】
解：直线，点坐标为，过点作轴的垂线交 直线于点可知点的坐标为，
以原点为圆心，长为半径画弧轴于点，，
，故点横坐标为，
按照这种方法可求得的坐标为，，故点坐标为，
以此类推便可求出点的横坐标为．
故选：A．
【点睛】
本题主要考查了一次函数的应用，解题的关键是做题时要注意数形结合思想的运用．
5．A
【解析】
【分析】
由k=-3＜0，利用一次函数的性质可得出y随x的增大而减小，结合1y2．
【详解】
解：∵k=-30，y随x的增大而增大；k2
【解析】
【分析】
从数来看，是当x取何值时，函数的值大于函数的值；从形来看，自变量取何值时，函数的图象位于函数的图形上方，这只要观察函数图象即可．
【详解】
由图象知，当x>2时，函数的图象位于函数的图形上方
所以关于的不等式的解集是x >2
故答案为：x >2
【点睛】
本题考查了一次函数与不等式的关系，数形结合是关键．
15．
【解析】
【分析】
根据题意确定有关b的不等式组，从而确定b的取值范围．
【详解】
解：∵一次函数y＝−3x＋b，若当x＝−2时，y＞0；当x＝2时，y＜0，
∴，
解得：−6＜b＜6，
故答案为：−6＜b＜6．
【点睛】
考查了一次函数图象与系数的关系，解题的关键是根据题意列出有关b的不等式组，难度不大．
16．
【解析】
【分析】
把代入，得出，再根据函数的图象即可得出不等式的解集．
【详解】
解：把代入，
解得：，
由图象可知，不等式的解集为：．
故答案为：．
【点睛】
本题主要考查了一次函数与一元一次不等式，本题是借助一次函数的图象解一元一次不等式，两个图象的“交点”是两个函数值大小关系的“分界点”，在“分界点”处函数值的大小发生了改变．
17．
【解析】
【分析】
作CD⊥AB于D，根据等腰直角三角形的性质得出BD=CD，由直线的解析式求得B（-4，0），A（0，3），即可求得OB=4，OA=3，利用勾股定理求得AB，设BD=CD=m，则AD=5-m，利用勾股定理表示出AC，然后根据三角形面积公式得到4×，解方程求得m，进一步即可求得C的坐标，然后根据待定系数法即可求得直线BC的解析式．
【详解】
解：作CD⊥AB于D，
∵∠ABC=45°，
∴∠DCB=45°，
∴BD=CD，
∵直线y=x+3交x轴于点B，交y轴于点A，
令x=0，则y=3；令y=0，则x=-4；
∴B（-4，0），A（0，3），
∴OB=4，OA=3，
∴，
设BD=CD=m，则AD=5-m，
∴，
由等积关系得，，
∴，
∴，
解得或m=20（舍去），
∴，
∴，
∴，
设直线BC的解析式为，
代入B（-4，0）得，，解得，
∴直线BC的解析式为，
故答案为：．
【点睛】
本题考查了一次函数图象上点的坐标特征，勾股定理的应用，三角形面积公式，待定系数法求一次函数的解析式，求得C的坐标是解题的关键．
18． （4，7） （2n-1，2n-1）
【解析】
【分析】
先由点B1（1，1）得到点A1的坐标，然后由B2（2，3）得到A2的坐标，进而得到直线的解析式，再令y=3求得点A3的坐标，从而求得点B3的坐标，⋯，再依次求得点Bn的坐标．
【详解】
解：∵点B1（1，1），B2（2，3），
∴点A1（1，0），A2（2，1），
将点A1（1，0），A2（2，1）代入y=kx+b得，
，解得：，
∴直线的解析式为y=x-1，
令y=3得，x-1=3，
∴x=4，
∴点A3的坐标为（4，3），
∴A3B3=4，
∴B3的坐标为（4，7），
令y=7得，x-1=7，
∴x=8，
∴点A4的坐标为（8，7），
∴A4B4=8，
∴B4的坐标为（8，15），⋯，
∴点Bn的坐标为（2n-1，2n-1），
故答案为：（4，7），（2n-1，2n-1）．
【点睛】
本题考查了一次函数图象上点的坐标特征、正方形的性质，解题的关键是通过一次函数图象上点的坐标特征求得系列点B的坐标．
19．，
【解析】
【分析】
过作轴，垂足为，由条件可求得，利用直角三角形的性质可求得，，可求得的坐标，同理可求得、的坐标，则可得出规律，可求得的坐标．
【详解】
如图，，△，△，都是边长为2的等边三角形，
，
，
在轴上，
轴，轴，
过作轴，垂足为，
点在在直线上，
设，
，
是面积为的等边三角形，
都是边长为的等边三角形，
，，
的坐标为，，
同理，、，，
的坐标为，，
故答案为，．
【点睛】
本题为规律型题目，利用等边三角形和直角三角形的性质求得的坐标，从而总结出点的坐标的规律是解题的关键.
20．（1）该网店甲种羽毛球每筒的售价为60元，乙种羽毛球每筒的售价为45元；（2）①进货方案有3种，具体见解析；②当m=78时，所获利润最大，最大利润为1390元．
【解析】
【分析】
（1）设甲种羽毛球每筒的售价为x元，乙种羽毛球每筒的售价为y元，由条件可列方程组，则可求得答案；
（2）①设购进甲种羽毛球m筒，则乙种羽毛球为（200﹣m）筒，由条件可得到关于m的不等式组，则可求得m的取值范围，且m为整数，则可求得m的值，即可求得进货方案；
②用m可表示出W，可得到关于m的一次函数，利用一次函数的性质可求得答案．
【详解】
（1）设甲种羽毛球每筒的售价为x元，乙种羽毛球每筒的售价为y元，
根据题意可得，解得，
答：该网店甲种羽毛球每筒的售价为60元，乙种羽毛球每筒的售价为45元；
（2）①若购进甲种羽毛球m筒，则乙种羽毛球为（200﹣m）筒，
根据题意可得 ，解得75＜m≤78，
∵m为整数，
∴m的值为76、77、78，
∴进货方案有3种，分别为：
方案一，购进甲种羽毛球76筒，乙种羽毛球为124筒，
方案二，购进甲种羽毛球77筒，乙种羽毛球为123筒，
方案一，购进甲种羽毛球78筒，乙种羽毛球为122筒；
②根据题意可得W=（60﹣50）m+（45﹣40）（200﹣m）=5m+1000，
∵5＞0，
∴W随m的增大而增大，且75＜m≤78，
∴当m=78时，W最大，W最大值为1390，
答：当m=78时，所获利润最大，最大利润为1390元．
【点睛】
本题考查了二元一次方程组的应用、一元一次不等式组的应用、一次函数的应用，弄清题意找准等量关系列出方程组、找准不等关系列出不等式组、找准各量之间的数量关系列出函数解析式是解题的关键.
21．（1）C的坐标是（﹣1，1）；（2）；（3）点P的坐标为（1，0）．
【解析】
【分析】
（1）作CD⊥x轴于D，BE⊥x轴于E，证明≌，根据全等三角形的性质得到CD＝AE，AD＝BE，求出点C的坐标；
（2）利用待定系数法求出直线BC的解析式，得到OM的长，根据梯形的面积公式、三角形的面积公式计算，得到答案；
（3）根据轴对称的最短路径问题作出点P，求出直线B的解析式，根据x轴上点的坐标特征求出点P的坐标．
【详解】
解：（1）如图，作CD⊥x轴于D，BE⊥x轴于E，
∴∠CAD+∠DCA＝90°，
∵∠BAC＝90°，
∴∠CAD+∠BAE＝90°，
∴∠BAE＝∠ACD，
在和中，
，
∴≌（AAS），
∴CD＝AE，AD＝BE，
∵A（2，0）、B（3，3），
∴OA＝2，OE＝BE＝3，
∴CD＝AE＝1，OD＝AD﹣OA＝1，
∴C的坐标是（﹣1，1）；
（2）如图，作BE⊥x轴于E，
设直线BC的解析式为y＝kx+b，
∵B点的坐标为（3，3），C点的坐标是（﹣1，1），
∴，
解得，，
∴直线BC的解析式为y＝x+，
当x＝0时，y＝，
∴OM＝，
∴的面积＝梯形MOEB的面积﹣的面积﹣的面积
＝×（+3）×3﹣×2×﹣×1×3
＝；
（3）如图，作M关于x轴的对称点（0，﹣），连接B，交x轴于点P，此时PB+PM=PB+P=B的值最小，
设直线B的解析式为y＝mx+n，
则，
解得，，
∴直线B的解析式为y＝x﹣，
点P在x轴上，当y＝0时，x＝1，
∴点P的坐标为（1，0）．
【点睛】
此题考查的是等腰直角三角形的性质、全等三角形的判定及性质、求一次函数解析式和求两线段和的最小值，掌握等腰直角三角形的性质、全等三角形的判定及性质、利用待定系数法求一次函数解析式和轴对称的最短路径问题是解决此题的关键．
22．（1）当m=1，n为任意实数时，这个函数是一次函数；（2）当m=1，n=−4时，这个函数是正比例函数.
【解析】
【分析】
（1）直接利用一次函数的定义分析得出答案；
（2）直接利用正比例函数的定义分析得出答案.
【详解】
(1)根据一次函数的定义，得：
2−|m|=1，
解得：m=±1.
又∵m+1≠0即m≠−1，
∴当m=1，n为任意实数时，这个函数是一次函数；
(2)根据正比例函数的定义，得：
2−|m|=1，n+4=0，
解得：m=±1，n=−4，
又∵m+1≠0即m≠−1，
∴当m=1，n=−4时，这个函数是正比例函数.
【点睛】
此题考查一次函数的定义，正比例函数的定义，解题关键在于利用其各定义进行解答.
23．直线l2的解析式为y=﹣x+4；（2）16.
【解析】
【分析】
（1）把x=2代入y=x，得y=1，求出A（2，1）．根据平移规律得出直线l3的解析式为y=x-4，求出B（0，-4）、C（4，-2）．设直线l2的解析式为y=kx+b，将A、C两点的坐标代入，利用待定系数法即可求出直线l2的解析式；
（2）根据直线l2的解析式求出D（0，4），得出BD=8，再利用三角形的面积公式即可求出△BDC的面积．
【详解】
（1）把x=2代入y=x，得y=1，
∴A的坐标为（2，1）．
∵将直线l1沿y轴向下平移4个单位长度，得到直线l3，
∴直线l3的解析式为y=x-4，
∴x=0时，y=-4，
∴B（0，-4）．
将y=-2代入y=x-4，得x=4，
∴点C的坐标为（4，-2）．
设直线l2的解析式为y=kx+b，
∵直线l2过A（2，1）、C（4，-2），
∴，解得，
∴直线l2的解析式为y=-x+4；
（2）∵y=-x+4，
∴x=0时，y=4，
∴D（0，4）．
∵B（0，-4），
∴BD=8，
∴△BDC的面积=×8×4=16．
【点睛】
本题考查了一次函数图象与几何变换，待定系数法求直线的解析式，一次函数图象上点的坐标特征，三角形的面积，正确求出求出直线l2的解析式是解题的关键．
24．（1）直线l2的函数解析式为y=x﹣5（2）3（3）在直线l2上存在点P（1，﹣4）或（9，4），使得△ADP面积是△ADC面积的2倍．
【解析】
【详解】
试题分析：（1）根据A、B的坐标，设直线l2的函数解析式为y=kx+b，利用待定系数发求出函数l2的解析式；
（2）由函数的解析式联立方程组，求解方程组，得到C点坐标，令y=-2x+4=0，求出D点坐标，然后求解三角形的面积；
（3）假设存在，根据两三角形面积间的关系|yP|=2|yC|，=4，再根据一次函数图像上点的坐标特征即可求出P点的坐标.
试题解析：（1）设直线l2的函数解析式为y=kx+b，
将A（5，0）、B（4，﹣1）代入y=kx+b，
，解得： ，
∴直线l2的函数解析式为y=x﹣5．
（2）联立两直线解析式成方程组，
，解得： ，
∴点C的坐标为（3，﹣2）．
当y=﹣2x+4=0时，x=2，
∴点D的坐标为（2，0）．
∴S△ADC=AD•|yC|=×（5﹣2）×2=3．
（3）假设存在．
∵△ADP面积是△ADC面积的2倍，
∴|yP|=2|yC|=4，
当y=x﹣5=﹣4时，x=1，
此时点P的坐标为（1，﹣4）；
当y=x﹣5=4时，x=9，
此时点P的坐标为（9，4）．
综上所述：在直线l2上存在点P（1，﹣4）或（9，4），使得△ADP面积是△ADC面积的2倍．
25．（1）大货车用8辆，小货车用10辆；（2）w=70a+11400（0≤a≤8且为整数）；（3）使总运费最少的调配方案是：3辆大货车、7辆小货车前往甲地；5辆大货车、3辆小货车前往乙地．最少运费为11610元．
【解析】
【分析】
（1）根据大、小两种货车共18辆，以及两种车所运的货物的和是192吨，据此即可列方程或方程组即可求解；
（2）首先表示出每种车中，每条路线中的费用，总运费为w元就是各个费用的和，据此即可写出函数关系式；
（3）根据运往甲地的物资不少于96吨，即可列出不等式求得a的范围，再根据a是整数，即可确定a的值，根据（2）中的函数关系，即可确定w的最小值，确定运输方案．
【详解】
（1）设大货车用x辆，则小货车用（18﹣x）辆，根据题意得：
14x+8（18﹣x）=192，解得：x=8，18﹣x=18﹣8=10．
答：大货车用8辆，小货车用10辆．
（2）设运往甲地的大货车是a，那么运往乙地的大货车就应该是（8﹣a），运往甲地的小货车是（10﹣a），运往乙地的小货车是10﹣（10﹣a），w=720a+800（8﹣a）+500（10﹣a）+650[10﹣（10﹣a）]=70a+11400（0≤a≤8且为整数）；
（3）14a+8（10﹣a）≥96，解得：a≥．
又∵0≤a≤8，
∴3≤a≤8 且为整数．
∵w=70a+11400，k=70＞0，w随a的增大而增大，
∴当a=3时，W最小，最小值为：W=70×3+11400=11610（元）．
答：使总运费最少的调配方案是：3辆大货车、7辆小货车前往甲地；5辆大货车、3辆小货车前往乙地．最少运费为11610元．
【点睛】
本题主要考查了一次函数和一元一次不等式的应用．解题的关键是根据实际意义列出函数关系式，从实际意义中找到对应的变量的值，利用待定系数法求出函数解析式，再根据自变量的值求算对应的函数值．
26．(1)； (2) (-4，6)； (3) (，)或(，)或(，)或(，)
【解析】
【分析】
(1)先求得点A、B的坐标，可求得OA、OB、AB的长，利用面积法即可求得OM的长；
(2)先画图，确定△BOP面积可以BO为底，P到y轴距离为高求得P到y轴距离，再分类讨论求得答案；
(3)分△OMP≌△PQO与△OMP≌△OQP两种情况讨论，结合图象分析即可求解．
【详解】
(1)对于直线，
令，则，令，则，
点A、B的坐标分别是(4，0)，(0，3)，
∴OA=4，OB=3，AB=，
∵，
∴；
(2)过P作PC⊥y轴于C，如图1，
∴OB•PC=6，
∴PC=4，
∴点P的横坐标为4或-4，
∵点P为直线上的一个动点且不与A、B重合，
∴横坐标为4时，与A重合，不合题意，
∴横坐标为-4时，纵坐标为：，
∴当点P坐标为(-4，6)时，△BOP的面积是6；
(3)存在，理由如下：
①当△OMP≌△PQO时，如图2和图3，
由(1)得，
∴PQ=OM=，即P点横坐标为或，
纵坐标为：或，
此时点P的坐标为(，)，(，)；
②当△OMP≌△OQP时，如图4和图5，
∴OQ=OM=，即即点P、点Q纵坐标为或，
由，解得：；
由，解得：；
此时点P的坐标为(，)，(，)；
综上所述，符合条件的点P的坐标为(，)或(，)或(，)或(，) ．
【点睛】
本题是一次函数与几何的综合题，考查了三角形及全等三角形的性质，体现了数形结合思想和分类讨论思想．解题关键是通过画图进行分类讨论．
27．（1）B（9，15）；（2）5；（3）存在，P（0，）
【解析】
【分析】
（1）根据点C的坐标确定b的值，利用待定系数法求出点A坐标即可解决问题；
（2）在Rt△BCD中，BC＝9，BD＝AB＝15，CD＝＝12，OD＝15﹣12＝3，设DE＝AE＝x，在Rt△DEO中，根据DE2＝OD2+OE2，构建方程即可解决问题；
（3）如图作点E关于y轴的对称点E′，连接BE′交y轴于P，此时△BPE的周长最小．利用待定系数法求出直线BE′的解析式即可解决问题；
【详解】
解：（1）∵AB＝15，四边形OABC是矩形，
∴OC＝AB＝15，
∴C（0，15），代入y＝y＝﹣x+b得到b＝15，
∴直线AC的解析式为y＝﹣x+15，
令y＝0，得到x＝9，
∴A（9，0），B（9，15）．
（2）在Rt△BCD中，BC＝9，BD＝AB＝15，
∴CD＝＝12，
∴OD＝15﹣12＝3，
设DE＝AE＝x，
在Rt△DEO中，∵DE2＝OD2+OE2，
∴x2＝32+（9﹣x）2，
∴x＝5，
∴AE＝5．
（3）如图作点E关于y轴的对称点E′，连接BE′交y轴于P，此时△BPE的周长最小．
∵E（4，0），
∴E′（﹣4，0），
设直线BE′的解析式为y＝kx+b，则有
解得，
∴直线BE′的解析式为y＝x+，
∴P（0，）．
故答案为（1）B（9，15）；（2）5；（3）存在，P（0，）.
【点睛】
本题考查一次函数综合题、矩形的性质、翻折变换、勾股定理等知识，解题的关键是熟练掌握待定系数法解决问题，学会利用轴对称解决最短问题，属于中考压轴题．
28．（1）A（1，1），B（3，0）；（2）存在一点C，C（－2，1）或（4，1）或（2，－1）；（3）在直线OA上，存在一点D， D（－，－）或（，）或（3，3）或（，），使得△DOB是等腰三角形．
【解析】
【分析】
（1）直线y＝－x＋与y＝x联立方程组求解，即可求出点A坐标，把y=0代入直线y＝－x＋即可求出点B坐标；
（2）分AO为对角线、AB为对角线、OB为对角线三种情况讨论，即可求出点C坐标；
（3）分OB＝OD、OD＝OB、OB＝DB三种情况讨论，结合勾股定理即可求出点D坐标．
【详解】
（1）∵直线y＝－x＋与y＝x相交于点A，
∴联立得，解得，
∴点A（1，1），
∵直线y＝－x＋与x轴交于点B，
∴令y＝0，得－x＋＝0，解得x＝3，
∴B（3，0），
（2）存在一点C，使得以O，A，B，C为顶点的四边形是平行四边形．
①如图1，过点A作平行于x轴的直线，过点O作平行于AB的直线，两直线交于点C，
∵AC∥x轴，OC∥AB，
∴四边形CABO是平行四边形，
∵A（1，1），B（3，0），∴AC＝OB＝3，
∴C（－2，1），
②如图2，过点A作平行于x轴的直线，过点B作平行于AO的直线，两直线交于点C，
∵AC∥x轴，BC∥AO，
∴四边形CAOB是平行四边形，
∵A（1，1），B（3，0），
∴AC＝OB＝3，∴C（4，1），
③如图3，过点O作平行于AB的直线，过点B作平行于AO的直线，两直线交于点C，
∵OC∥AB，BC∥AO，
∴四边形CBAO是平行四边形，
∵A（1，1），B（3，0），
∴AO＝BC，OC＝AB，
作AE⊥OB，CF⊥OB，易得OE＝EF＝FB＝1，
∴C（2，－1），
（3）在直线OA上，存在一点D，使得△DOB是等腰三角形，
①如图4，当OB＝OD时，作DE⊥x轴，交x轴于点E
∵OB＝3，点D在OA上，∠DOE＝45°
∴DE＝OE＝，
∴D（－，－），
②如图5，当OD＝OB时，作DE⊥x轴，交x轴于点E
∵OB＝3，点D在OA上，∠DOE＝45°
∴DE＝OE＝，
∴D（，），
③如图6，当OB＝DB时，
∵∠AOB＝∠ODB＝45°，
∴DB⊥OB，
∵OB＝3，
∴D（3，3），
④如图7，当DO＝DB时，作DE⊥x轴，交x轴于点E
∵∠AOB＝∠OBD＝45°，
∴OD⊥DB，
∵OB＝3，
∴OE＝，AE＝，
∴D（，）．
综上所述，在直线OA上，存在点D（－，－），D（，），D（3，3）或D（，），使得△DOB是等腰三角形．
【点睛】
本题为与几何有关一次函数的综合题，考查了一次函数与方程（组）的关系，确定平行四边形第四个顶点坐标，等腰三角形第三个顶点的坐标，勾股定理等知识，综合性强，理解一次函数与方程（组）的关系，能进行分类讨论是解题关键．
29．（1）5；（2）直线AC的解析式y=﹣x+；（3）①；②t=或．
【解析】
【分析】
（1）Rt△AOH中利用勾股定理即可求得菱形的边长；
（2）根据（1）即可求的OC的长，则C的坐标即可求得，利用待定系数法即可求得直线AC的解析式；
（3）根据S△ABC=S△AMB+S△BMC求得M到直线BC的距离为h，然后分成P在AM上和在MC上两种情况讨论，利用三角形的面积公式求解．
【详解】
解：（1）Rt△AOH中，
，
所以菱形边长为5；
故答案为5；
（2）∵四边形ABCO是菱形，
∴OC=OA=AB=5，即C（5，0）．
设直线AC的解析式y=kx+b，函数图象过点A、C，得
，解得，
直线AC的解析式；
（3）设M到直线BC的距离为h，
当x=0时，y=，即M（0，），，
由S△ABC=S△AMB+SBMC=AB•OH=AB•HM+BC•h，
×5×4=×5×+×5h，解得h=，
①当0＜t＜时，BP=BA﹣AP=5﹣2t，HM=OH﹣OM=，
S=BP•HM=×（5﹣2t）=﹣t+；
当＜t≤5时，BP=2t﹣5，h=，
S=BP•h=×（2t﹣5）=t﹣，
∴
②把S=3代入①中的函数解析式得，3=﹣t+，
解得：t=，
把S=3代入①的解析式得，3=t﹣，
解得：t=．
∴t=或．
【点睛】
本题考查了待定系数法求一次函数的解析式以及菱形的性质，根据三角形的面积关系求得M到直线BC的距离h是关键．
30．（1）b=；（2）①△APQ的面积S与t的函数关系式为S=﹣t+或S=t﹣；②7＜t＜9或9＜t＜11，③存在，当t的值为3或9+3或9﹣3或6时，△APQ为等腰三角形．
【解析】
【详解】
分析：（1）把P(m,3)的坐标代入直线的解析式即可求得P的坐标，然后根据待定系数法即可求得b；
（2）根据直线的解析式得出C的坐标，①根据题意得出，然后根据即可求得的面积S与t的函数关系式；②通过解不等式或即可求得7