2020-2021学年天津市津南区七年级（下）期末数学试卷及答案

这是一份2020-2021学年天津市津南区七年级（下）期末数学试卷及答案，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）16的算术平方根是（ ）
A．4B．﹣4C．±4D．2
2．（3分）在平面直角坐标中，点P（﹣3，5）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
3．（3分）估计的值应在（ ）
A．3与4之间B．4与5之间C．5与6之间D．6与7之间
4．（3分）实数﹣8，3.14159265，﹣，π，，中，无理数的个数是（ ）
A．0B．1C．2D．3
5．（3分）如图，直线a∥b，∠1＝53°，则∠3的大小是（ ）
A．53°B．83°C．103°D．127°
6．（3分）如图，要使DE∥BC，那么应满足（ ）
A．∠A＝∠CB．∠C＝∠BC．∠B+∠C＝180°D．∠ADE＝∠B
7．（3分）下面的调查，适合抽样调查的是（ ）
A．了解全国中小学生课外阅读情况
B．检测长征运载火箭的零部件质量情况
C．了解某班学生的身高情况
D．了解某班同学每周体育锻炼的时间
8．（3分）已知a＞b，则下列不等式成立的是（ ）
A．a+5＜b+5B．a﹣5＜b﹣5C．D．﹣5a＜﹣5b
9．（3分）方程组的解是（ ）
A．B．C．D．
10．（3分）有48支队520名运动员参加篮球、排球比赛，其中每支篮球队10人，每支排球队12人，每名运动员只能参加一项比赛，设篮球队有x支参赛，排球队有y支参赛，则下面所列方程组正确的是（ ）
A．B．
C．D．
11．（3分）下列命题：①经过直线外一点，有且只有一条直线与这条直线垂直；②内错角相等；③相等的角是对顶角；④如果两条直线都与第三条直线平行，那么这两条直线也互相平行．其中，真命题有（ ）
A．3个B．2个C．1个D．0个
12．（3分）已知关于x的一元一次不等式组有2个整数解，若a为整数，则a的值为（ ）
A．5B．6C．6或7D．7或8
二、填空题（本大题共6小题，每小题3分，共18分）
13．（3分）﹣的相反数为 ，﹣1.7的绝对值是 ．
14．（3分）计算的结果等于 ．
15．（3分）如图，在象棋盘上建立平面直角坐标系，若“将”位于点（0，﹣2），“炮”位于点（﹣3，1），则“象”位于点的坐标是 ．
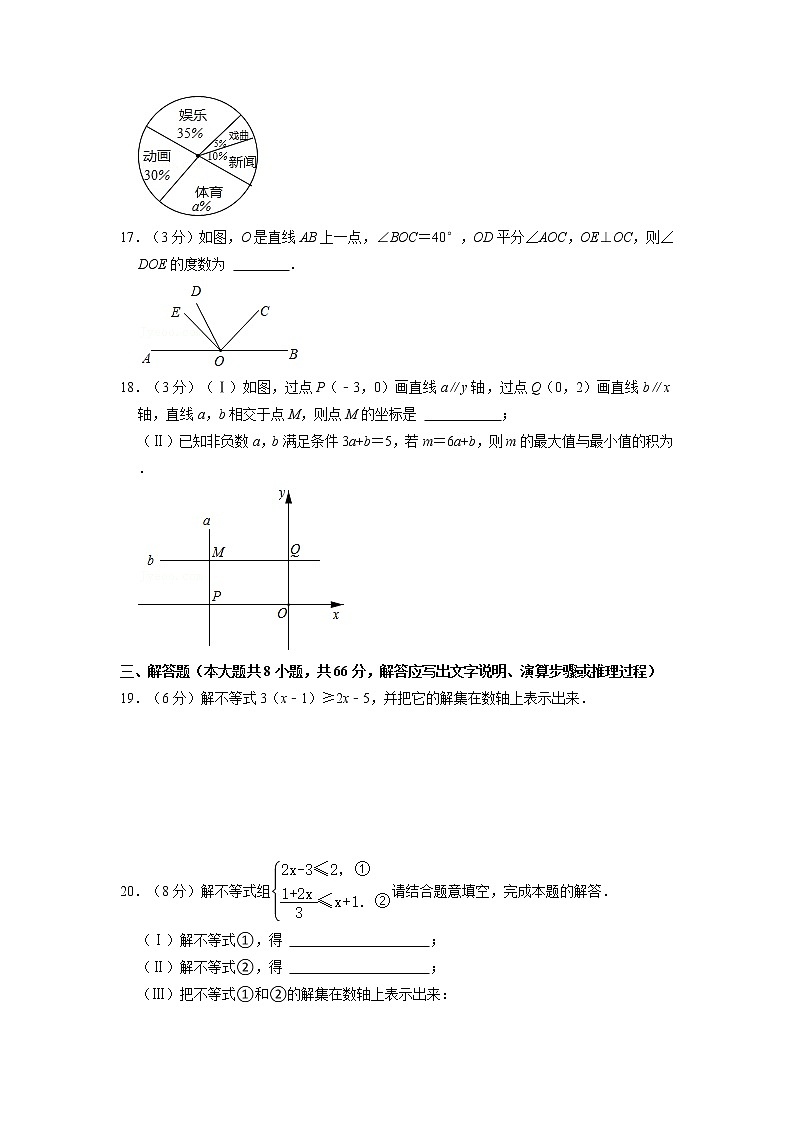
16．（3分）为调查某校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取部分学生进行调查，并根据调查数据画出如图所示的扇形统计图．
根据图中提供的信息，回答下列问题：
（Ⅰ）喜爱体育节目对应扇形图中的a的值为 ；
（Ⅱ）在扇形统计图中，喜欢娱乐节目对应扇形图的圆心角的大小为 （度）．
17．（3分）如图，O是直线AB上一点，∠BOC＝40°，OD平分∠AOC，OE⊥OC，则∠DOE的度数为 ．
18．（3分）（Ⅰ）如图，过点P（﹣3，0）画直线a∥y轴，过点Q（0，2）画直线b∥x轴，直线a，b相交于点M，则点M的坐标是 ；
（Ⅱ）已知非负数a，b满足条件3a+b＝5，若m＝6a+b，则m的最大值与最小值的积为 ．
三、解答题（本大题共8小题，共66分，解答应写出文字说明、演算步骤或推理过程）
19．（6分）解不等式3（x﹣1）≥2x﹣5，并把它的解集在数轴上表示出来．
20．（8分）解不等式组请结合题意填空，完成本题的解答．
（Ⅰ）解不等式①，得 ；
（Ⅱ）解不等式②，得 ；
（Ⅲ）把不等式①和②的解集在数轴上表示出来：
（Ⅳ）原不等式组的解集为 ．
21．（12分）解方程组：
（Ⅰ）； （Ⅱ）．
22．（6分）如图，三角形ABC的三个顶点坐标为A（﹣1，0），B（﹣3，﹣2），C（0，﹣3）．将这个三角形向右平移3个单位长度，再向上平移1个单位长度，得三角形A′B′C′，点A′，B′，C′分别是平移后点A，B，C的对应点．
（Ⅰ）画出平移后的三角形A′B′C′；
（Ⅱ）写出点B′和点C′的坐标；
（Ⅲ）写出线段AA′与CC′的位置和大小关系．
23．（6分）某校组织了一次“疫情防控知识”专题网上学习，并进行了一次全校2500名学生都参加的网上测试．阅卷后，教务处随机抽取100份答卷进行分析统计，绘制了频数分布表和频数分布直方图（不完整），请结合图表信息回答下列问题：
（Ⅰ）a＝ ，b＝ ，n＝ ，频率分布表的组距是 ；
（Ⅱ）补全频数分布直方图；
（Ⅲ）全校学生参加网上测试，成绩x在81≤x＜101范围内的学生约有多少人？
24．（10分）（Ⅰ）填空，并在括号内标注理由．
已知：如图①，DE∥BC，∠AED+∠DFC＝180°，求证DF∥AC．
证明：DE∥BC，（已知）
∴∠AED＝∠ ；（ ）
又∵∠AED+∠DFC＝180°，（已知）
∴∠ +∠ ＝180°．
∴DF∥AC．（ ）
（Ⅱ）如图②，AB∥CD，EF⊥AB，垂足为E，与CD相交于点F，点M在直线CD上，且∠FEM＝32°，MN平分∠CME，与AB相交于点N，求∠CMN的度数．
25．（8分）某校七年级学生去看演出，甲种票每张24元，乙种票每张18元．
（Ⅰ）七年一班35名学生购票恰好用去750元，问甲乙两种票各买了多少张？
设甲种票买了x张，乙种票买了y张．
根据题意，列方程组．
解这个方程组，得．
答： ．
（Ⅱ）该校七年级共有420名学生，购买演出票的总费用不超过9000元．请问甲种票最多购买多少张？
26．（10分）在平面直角坐标系中，O为原点，点A（0，﹣3），B（﹣2，0）．
（Ⅰ）如图①，则三角形OAB的面积为 ；
（Ⅱ）如图②，将线段AB向右平移5个单位长度，再向上平移4个单位长度，得到平移后的线段A′B′．连接OA′，OB′．
①求三角形OA′B′的面积；
②P（﹣1，m）（m＞0）是一动点，若S三角形POB＝10，请直接写出点P坐标．
参考答案
1-5．ABBCD 6-10．DADAC 11-12．BD
13．，﹣1.7 14．﹣ 15．（2，﹣2）
16．20；126 17．20° 18．（﹣3，2）；5
19．解：3（x﹣1）≥2x﹣5，
去括号：3x﹣3≥2x﹣5，
移项得：3x﹣2x≥﹣5+3，
合并同类项得x≥﹣2，
所以原不等式的解是：x≥﹣2，
在数轴上表示为：
．
20．解：解不等式①得：x≤，
解不等式②得：x≥﹣2，
把不等式①和②的解集在数轴上表示出来：
，
原不等式组的解集为：﹣2≤x≤．
21．解：（Ⅰ），
把①代入②，得3x+2（2x﹣5）＝4，
解得x＝2，
把x＝2代入①，得y＝﹣1，
故方程组的解为；
（Ⅱ），
①﹣②，得4y＝28，
解答y＝7，
把y＝7代入①，得3x﹣7＝8，
解得x＝5，
故方程组的解为．
22．解：（Ⅰ）如图，△A′B′C′为所作；
（Ⅱ）B′（0，﹣1），C′（3，﹣2）；
（Ⅲ）AA′∥CC′；AA′＝CC′．
23．解：（Ⅰ）a＝100×0.1＝10，
b＝100﹣10﹣18﹣35﹣12＝25，
n＝25÷100＝0.25，
频率分布表的组距是61﹣51＝10，
（Ⅱ）如图，即为补充完整的频数分布直方图；
（Ⅲ）∵2500×（0.35+0.12）＝1175（人），
∴成绩x在81≤x＜101范围内的学生约有1175人．
24．（Ⅰ）证明：DE∥BC（已知），
∴∠AED＝∠C（两直线平行，同位角相等），
又∵∠AED+∠DFC＝180°（已知），
∴∠DFC+∠C＝180°，
∴DF∥AC（同旁内角互补，两直线平行）．
（Ⅱ）解：∵EF⊥AB，∴∠AEF＝90°，
∵∠FEM＝32°，∴∠AEM＝90°﹣∠FEM＝90°﹣32°＝58°，
∵AB∥CD，∴∠CME+∠AEM＝180°，∴∠CME＝180°﹣58°＝122°，
∵MN平分∠CME，∴∠CMN＝∠CME＝×122°＝61°．
25．解：（Ⅰ）设甲种票买x张，乙种票买y张，根据题意得：，
解得
答：甲种票买20张，乙种票买15张．
（Ⅱ）可设甲种票购买m张，则乙种票买了（420﹣m）张，根据题意得：
24m+18（420﹣m）≤9000，
解得m≤240．
故甲种票最多购买240张．
26．解：（Ⅰ）∵A（0，﹣3），B（﹣2，0），∴OA＝3，OB＝2，
∴S△AOB＝×2×3＝3，
（Ⅱ）①如图，S△A′B′O＝4×5﹣×3×4﹣×2×3﹣×5×1＝．
②由题意，×2×m＝10，
∴m＝10，
∴P（﹣1，10）