2023年高考数学(文数)一轮复习课时36《由三视图求几何体面积、体积》达标练习（2份，答案版+教师版）

这是一份2023年高考数学(文数)一轮复习课时36《由三视图求几何体面积、体积》达标练习（2份，答案版+教师版），文件包含2023年高考数学文数一轮复习课时36《由三视图求几何体面积体积》达标练习含详解doc、2023年高考数学文数一轮复习课时36《由三视图求几何体面积体积》达标练习教师版doc等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。

一、选择题
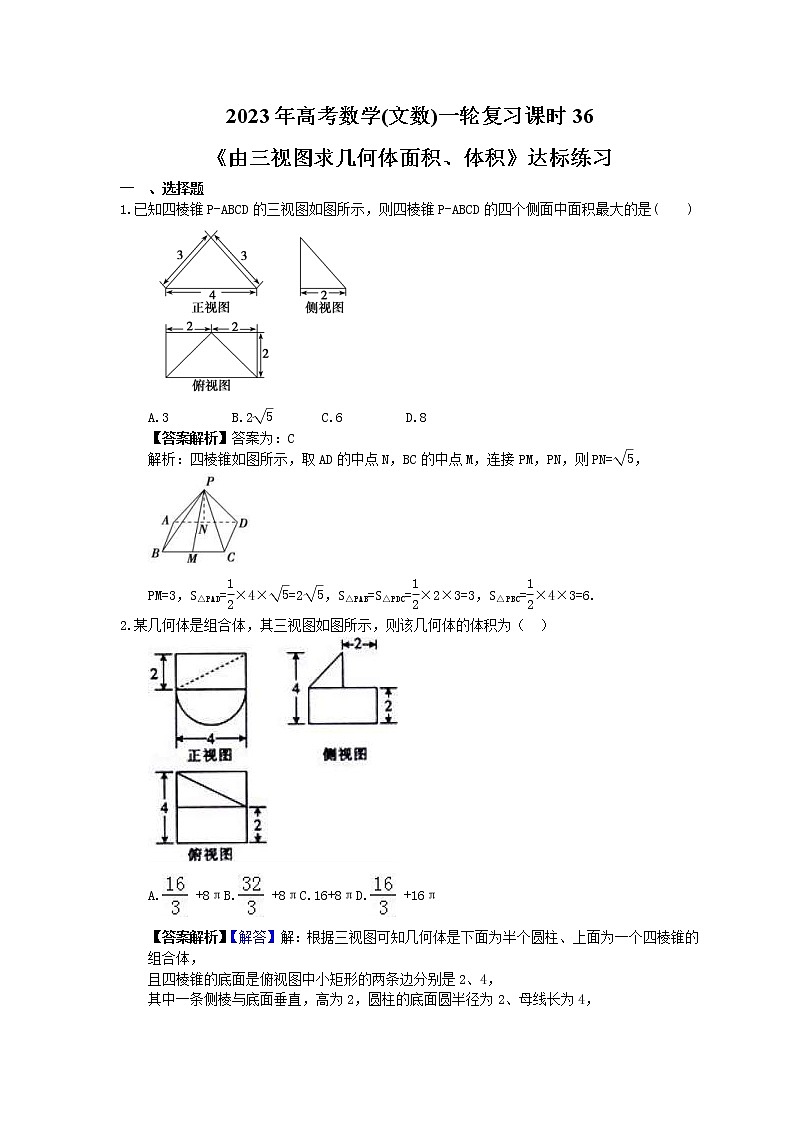
已知四棱锥P-ABCD的三视图如图所示，则四棱锥P-ABCD的四个侧面中面积最大的是( )
A.3 B.2eq \r(5) C.6 D.8
【答案解析】答案为：C
解析：四棱锥如图所示，取AD的中点N，BC的中点M，连接PM，PN，则PN=eq \r(5)，
PM=3，S△PAD=eq \f(1,2)×4×eq \r(5)=2eq \r(5)，S△PAB=S△PDC=eq \f(1,2)×2×3=3，S△PBC=eq \f(1,2)×4×3=6.
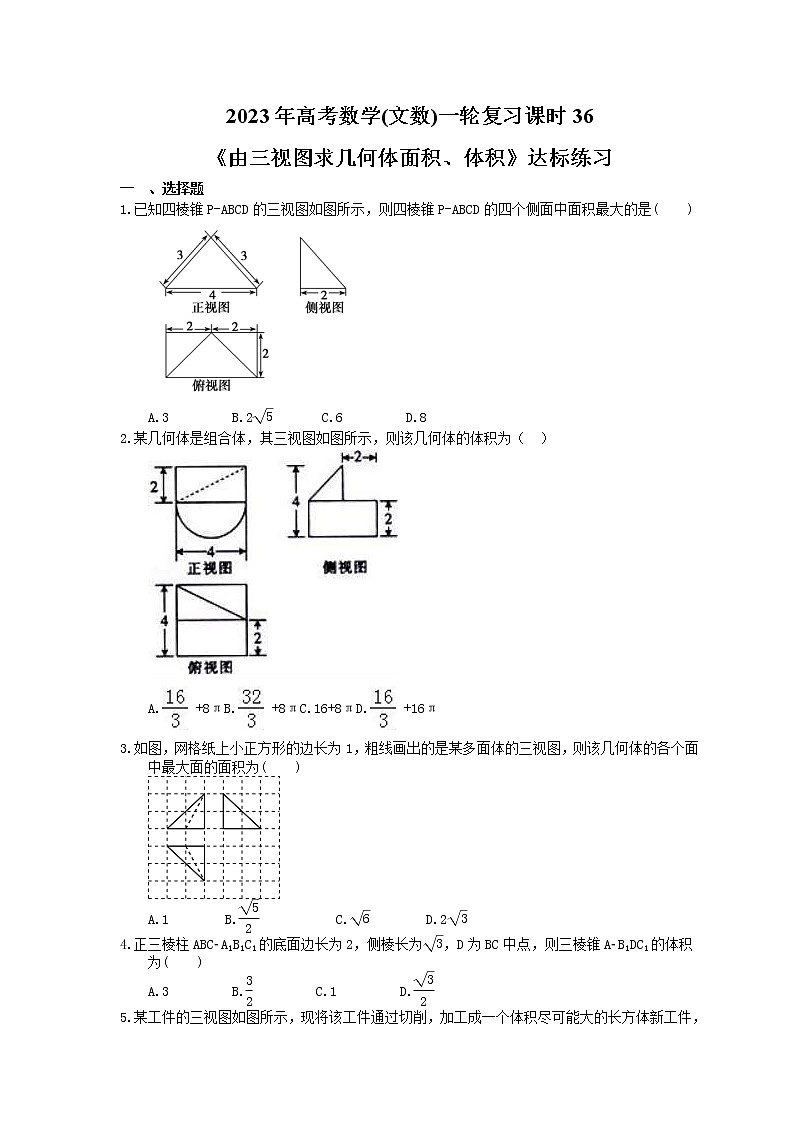
某几何体是组合体，其三视图如图所示，则该几何体的体积为（ ）

A. +8πB. +8πC.16+8πD. +16π
【答案解析】【解答】解：根据三视图可知几何体是下面为半个圆柱、上面为一个四棱锥的组合体，
且四棱锥的底面是俯视图中小矩形的两条边分别是2、4，
其中一条侧棱与底面垂直，高为2，圆柱的底面圆半径为2、母线长为4，
所以该几何体的体积为V=×2×4×2+×π×22×4=+8π．故选：A．
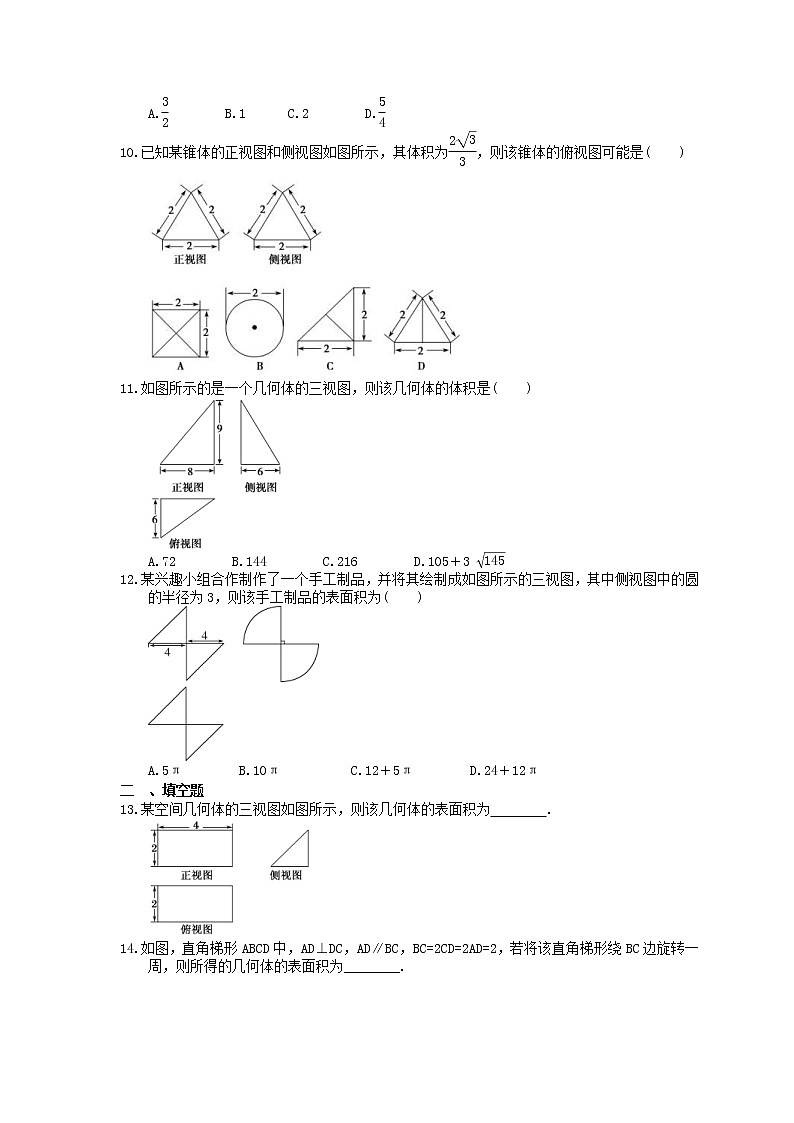
如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该几何体的各个面中最大面的面积为( )
A.1 B.eq \f(\r(5),2) C.eq \r(6) D.2eq \r(3)
【答案解析】答案为：D
解析：由题意知，该几何体的直观图为三棱锥A－BCD，
如图，其最大面的表面是边长为2 eq \r(2)的等边三角形，
故其面积为eq \f(1,2)×2 eq \r(2)×eq \r(2 \r(2)2－\r(2)2)=2 eq \r(3).
正三棱柱ABC­A1B1C1的底面边长为2，侧棱长为eq \r(3)，D为BC中点，则三棱锥A­B1DC1的体积为( )
A.3 B.eq \f(3,2) C.1 D.eq \f(\r(3),2)
【答案解析】答案为：C；
解析：∵D是等边三角形ABC的边BC的中点，∴AD⊥BC.
又ABC­A1B1C1为正三棱柱，∴AD⊥平面BB1C1C.
又四边形BB1C1C为矩形，∴S△DB1C1=eq \f(1,2)S四边形BB1C1C=eq \f(1,2)×2×eq \r(3)=eq \r(3).
又AD=2×eq \f(\r(3),2)=eq \r(3)，∴VA­B1DC1=eq \f(1,3)S△B1DC1·AD=eq \f(1,3)×eq \r(3)×eq \r(3)=1.故选C.
某工件的三视图如图所示，现将该工件通过切削，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为(材料利用率=eq \f(新工件的体积,原工件的体积))( )
A.eq \f(8,9π) B.eq \f(16,9π) C.eq \f(4（\r(2)－1）3,π) D.eq \f(12（\r(2)－1）3,π)
【答案解析】答案为：A；
解析：依题意知，题中的工件形状是一个底面半径为1、高为2的圆锥，
设新工件的长、宽、高分别为a，b，c，截去的小圆锥的底面半径、高分别为r，h，
则有a2＋b2=4r2，h=2r，该长方体的体积为abc=ab(2－2r)≤eq \f(（a2＋b2）（2－2r）,2)
=4r2(1－r).记f(r)=4r2(1－r)，则有f′(r)=4r(2－3r)，当0＜r＜eq \f(2,3)时，f′(r)＞0，
当eq \f(2,3)＜r＜1时，f′(r)＜0，因此f(r)=4r2(1－r)的最大值是f（eq \f(2,3)）=eq \f(16,27)，
则原工件材料的利用率为eq \f(16,27)÷eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)π×12×2))=eq \f(8,9π)，选A.
一个正三棱柱的正(主)视图和俯视图如图所示，则这个三棱柱的侧(左)视图的面积为( )
A.6eq \r(3) B.8 C.8eq \r(3) D.12
【答案解析】答案为：A
解析：该三棱柱的侧(左)视图为一个矩形，由“长对正，高平齐，宽相等”的原理知，
其侧(左)视图的底边长为俯视图中正三角形的高，即为2eq \r(3)，侧(左)视图的高为3，
故其侧(左)视图的面积为S=2eq \r(3)×3=6eq \r(3).故选A.
底面水平放置的正三棱柱的所有棱长均为2，当其正视图有最大面积时，其侧视图的面积为( )
A.2eq \r(3) B.3 C.eq \r(3) D.4
【答案解析】答案为：A
解析：当正视图的面积最大时，可以按如图所示放置，可知其侧面的面积S侧=2eq \r(3).
一个几何体的三视图如图所示，则该几何体的体积为( )
A.eq \f(16,3) B.eq \f(20,3) C.eq \f(15,2) D.eq \f(13,2)
【答案解析】答案为：D
解析：该几何体可视为正方体截去两个三棱锥所得，如图所示，
所以其体积为23－eq \f(1,3)×eq \f(1,2)×2×2×2－eq \f(1,3)×eq \f(1,2)×1×1×1=eq \f(13,2).故选D.
如图，在底面边长为1，高为2的正四棱柱ABCD­A1B1C1D1(底面ABCD是正方形，侧棱AA1⊥底面ABCD)中，点P是正方形A1B1C1D1内一点，则三棱锥P­BCD的正视图与俯视图的面积之和的最小值为( )
A.eq \f(3,2) B.1 C.2 D.eq \f(5,4)
【答案解析】答案为：A；
解析：由题易知，其正视图面积为eq \f(1,2)×1×2=1.当顶点P在底面ABCD上的投影在△BCD内部或其边上时，俯视图的面积最小，最小值为S△BCD=eq \f(1,2)×1×1=eq \f(1,2)，所以三棱锥P­BCD的正视图与俯视图的面积之和的最小值为1＋eq \f(1,2)=eq \f(3,2)，故选A.
已知某锥体的正视图和侧视图如图所示，其体积为eq \f(2\r(3),3)，则该锥体的俯视图可能是( )
【答案解析】答案为：C
解析：由正视图得该锥体的高是h=eq \r(22－12)=eq \r(3)，因为该锥体的体积为eq \f(2\r(3),3)，所以该锥体的底面面积是S=eq \f(\f(2\r(3),3),\f(1,3)h)=eq \f(\f(2\r(3),3),\f(\r(3),3))=2，A项的正方形的面积是2×2=4，B项的圆的面积是π×12=π，C项的大三角形的面积是eq \f(1,2)×2×2=2，D项不可能是该锥体的俯视图，故选C.
如图所示的是一个几何体的三视图，则该几何体的体积是( )
A.72 B.144 C.216 D.105＋3 eq \r(145)
【答案解析】答案为：A；
解析：由三视图知，该几何体是一个三棱锥，底面直角三角形的面积为eq \f(1,2)×6×8=24，
设三棱锥的高为9，所以该几何体的体积为eq \f(1,3)×24×9=72，故选A.
某兴趣小组合作制作了一个手工制品，并将其绘制成如图所示的三视图，其中侧视图中的圆的半径为3，则该手工制品的表面积为( )
A.5π B.10π C.12＋5π D.24＋12π
【答案解析】答案为：D；
解析：由三视图可知，该手工制品是由两部分构成，每一部分都是相同圆锥的四分之一，
且圆锥的底面半径为3，高为4，故母线长为5，故每部分的表面积为
2×eq \f(1,2)×4×3＋eq \f(1,4)×eq \f(1,2)×6π×5＋eq \f(1,4)×9π=12＋6π，故两部分表面积为24＋12π.
二、填空题
某空间几何体的三视图如图所示，则该几何体的表面积为 .
【答案解析】答案为：20＋8eq \r(2).
解析：由三视图可知该几何体是底面为等腰直角三角形的直三棱柱，如图.
则该几何体的表面积为S=2×eq \f(1,2)×2×2＋4×2×2＋2eq \r(2)×4=20＋8eq \r(2).
如图，直角梯形ABCD中，AD⊥DC，AD∥BC，BC=2CD=2AD=2，若将该直角梯形绕BC边旋转一周，则所得的几何体的表面积为________.
【答案解析】答案为：(eq \r(2)＋3)π.
解析：根据题意可知，该几何体的上半部分为圆锥(底面半径为1，高为1)，
下半部分为圆柱(底面半径为1，高为1)，如图所示，
则所得几何体的表面积为圆锥侧面积、圆柱的侧面积以及圆柱的下底面面积之和，
即表面积为π×1×eq \r(12＋12)＋2π×12＋π×12=(eq \r(2)＋3)π.
某空间几何体的三视图如图所示，则该几何体的体积为________.
【答案解析】答案为：eq \f(8－π,3).
解析：由题意得到几何体的直观图如图所示，
即从四棱锥P-ABCD中挖去了一个半圆锥.
其体积V=eq \f(1,3)×2×2×2－eq \f(1,2)×eq \f(1,3)×π×12×2=eq \f(8－π,3).
在《九章算术》中有称为“羡除”的五面体体积的求法．现有一个类似于“羡除”的有三条棱互相平行的五面体，其三视图如图所示，则该五面体的体积为________．
【答案解析】答案为：24
解析：由三视图可得，该几何体为如图所示的五面体ABCEFD，
其中，底面ABC为直角三角形，且∠BAC=90°，AB=4，AC=3，侧棱DB，EC，FA与底面垂直，且DB=2，EC=FA=5.过点D作DH∥BC，DG∥BA，交EC，FA分别于点H，G，
则棱柱ABC­DHG为直棱柱，四棱锥D­EFGH的底面为矩形EFGH，高为BA.
所以V五面体ABCEFD=VABC­DHG＋VD­EFGH=（eq \f(1,2)×4×3）×2＋eq \f(1,3)×32×4=24.故答案为24.