北师大版七年级下册期末专题04 三角形（原卷+解析）

这是一份北师大版七年级下册期末专题04 三角形（原卷+解析），文件包含专题04三角形解析版docx、专题04三角形原卷版docx等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。
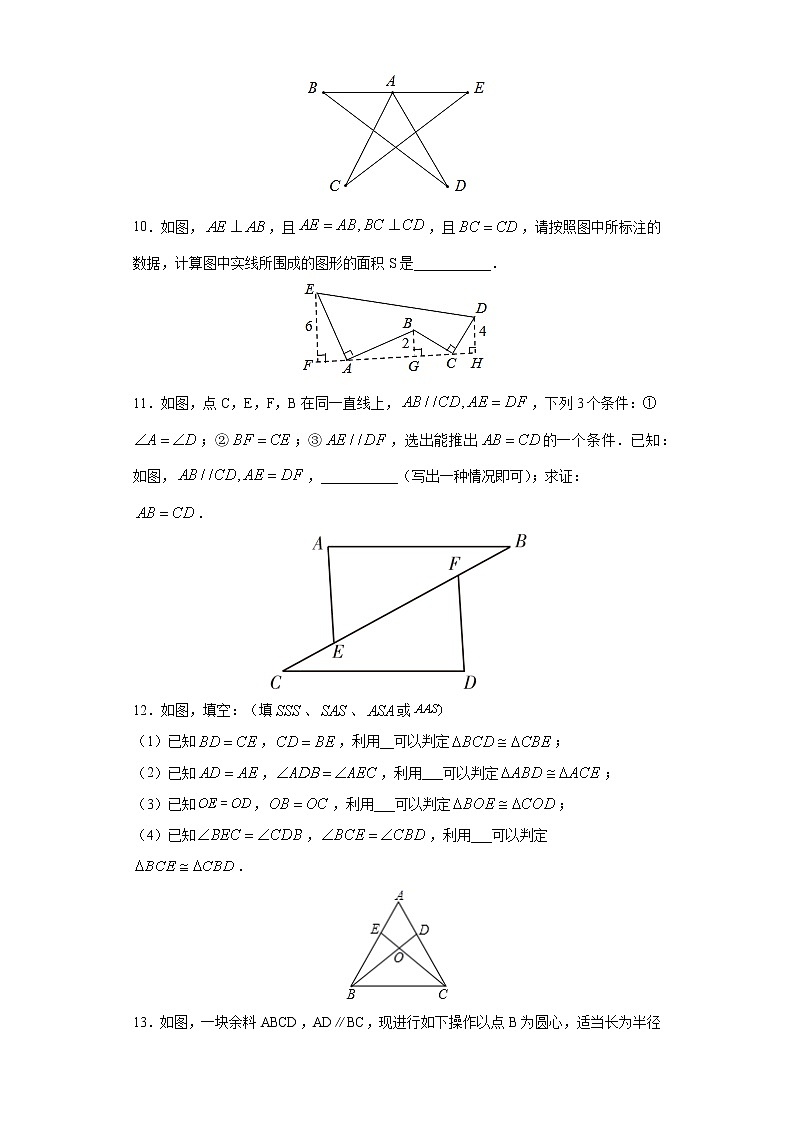
专题04  三角形学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列每组数表示3根小木棒的长度，3根小木棒能摆成三角形的一组是　　A．1cm，2cm，3cm B．2cm，3cm，4cm C．2cm，3cm，5cm D．2cm，3cm，6cm【答案】B【解析】、，不能构成三角形；、，能构成三角形；、，不能构成三角形；、，不能构成三角形．故选：．2．三角形的中线和角平分线都是　　A．直线 B．射线 C．线段 D．以上都有可能【答案】C【解析】解：三角形的中线和角平分线都是线段，故选：．3．如图，，3分别与、相交，点A为上一点，于点B，若，则的度数为（    ）A．28° B．42° C．38° D．32°【答案】B【解析】解：如图，、交于点，∵，，∴，∵，∴，∴．故选：D．4．下列说法中正确的是（      ）A．两个面积相等的图形，一定是全等图形 B．两个等边三角形是全等图形C．两个全等图形的面积一定相等 D．若两个图形周长相等，则它们一定是全等图形【答案】C【解析】解：A、两个面积相等的图形不一定是全等图形，故A错误；B、两个等边三角形不一定是全等图形，故B错误；C、两个全等图形的面积一定相等，正确；D、若两个图形的周长相等，则它们不一定是全等形，故D错误；故选：C．5．如图，点在同一直线上，，则等于（    ）A．4 B．5 C．6 D．7【答案】A【解析】解：∵△ABC≌△DEF，DF=4，∴AC=DF=4，故选：A．6．如图，已知，用直尺和圆规按照以下步骤作图：①以点为圆心，任意长为半径画弧，分别交、于点、；②画射线，以点为圆心，长为半径画弧，交于点；③以点为圆心，长为半径画弧，与第②步中所画的弧相交于点；④过点画射线；根据以上操作，可以判定≌，其判定的依据是（    ）A．SSS B．SAS C．ASA D．HL【答案】A【解析】解：由步骤②得半径= ，由步骤③半径= ，半径OD=，在和中，∴≌（SSS）．故选择A．7．已知：如图，点D，E分别在，上，，添加一个条件，不能判定的是（    ）A． B． C． D．【答案】A【解析】∵不符合任何一个判定定理，不能判定∴A符合题意；∵,符合SAS判定定理，能判定∴B不符合题意；∵,符合ASA判定定理，能判定∴C不符合题意；∵,符合AAS判定定理，能判定∴D不符合题意；故选A．8．如图，、是的角平分线，、相交于点F，已知，则下列说法中正确的个数是（    ）①；②；③；④．A．1 B．2 C．3 D．4【答案】B【解析】解：①假设AF=FC．则∠1=∠4．∵AD、CE是△ABC的角平分线，∴∠BAC=2∠1，∠BCA=2∠4，∴∠BAC=∠BCA．∴当∠BAC≠∠BCA时，该结论不成立；故①不一定正确；②假设△AEF≌△CDF，则∠2=∠3．同①，当∠BAC=∠BCA时，该结论成立，∴当∠BAC≠∠BCA时，该结论不成立；故②不一定正确；③如图，在AC上取AG=AE，连接FG，∵AD平分∠BAC，∴∠1=∠2，在△AEF与△AGF中，∴△AEF≌△AGF（SAS），∴∠AFE=∠AFG；∵AD、CE分别平分∠BAC、∠ACB，∴∠4+∠1=∠ACB+∠BAC=（∠ACB+∠BAC）=（180°-∠B）=60°，则∠AFC=180°-（∠4+∠1）=120°；∴∠AFC=∠DFE=120°，∠AFE=∠CFD=∠AFG=60°，则∠CFG=60°，∴∠CFD=∠CFG，在△GFC与△DFC中，，∴△GFC≌△DFC（ASA），∴DC=GC，∵AC=AG+GC，∴AC=AE+CD．故③正确； ④由③知，∠AFC=180°-∠ECA-∠DAC=120°，即∠AFC=120°；故④正确；综上所述，正确的结论有2个．故选：B．  二、填空题9．如图，____________．【答案】【解析】∵∠BAC和∠DAE分别是△ACE和△ABD的外角，∴∠BAC=∠C+∠E，∠DAE=∠B+∠D，∴∠CAD+∠BAC+∠DAE=180°，故答案为：180°10．如图，，且，且，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是___________．【答案】50【解析】解：∵AE⊥AB，EF⊥AF，BG⊥AG，∴∠F=∠AGB=∠EAB=90°，∴∠FEA+∠EAF=90°，∠EAF+∠BAG=90°，∴∠FEA=∠BAG，在△FEA和△GAB中，∵，∴△FEA≌△GAB（AAS），∴AG=EF=6，AF=BG=2，同理CG=DH=4，BG=CH=2，∴FH=2+6+4+2=14，∴梯形EFHD的面积是×（EF+DH）×FH=×（6+4）×14=70，∴阴影部分的面积是S梯形EFHD-S△EFA-S△ABC-S△DHC=70-×6×2-×（6+4）×2-×4×2=50．故答案为50．11．如图，点C，E，F，B在同一直线上，，下列3个条件：①；②；③，选出能推出的一个条件．已知：如图，，___________（写出一种情况即可）；求证：．【答案】①或③；见解析【解析】.法一：若选①，证明如下：∵，∴．∵，∴．∴．法二：若选③，证明如下：∵，∴．∵，∴．∵，∴．∴．12．如图，填空：（填、、或（1）已知，，利用__可以判定；（2）已知，，利用___可以判定；（3）已知，，利用___可以判定；（4）已知，，利用___可以判定．【答案】                【解析】解：（1），，为公共边，；（2），，为公共角，；（3），，（对顶角相等），；（4），，为公共边，．故答案为：（1）；（2）；（3）；（4）．13．如图，一块余料ABCD，AD∥BC，现进行如下操作以点B为圆心，适当长为半径作圆弧，分别交BA，BC于点G，H；再分别以点G，H为圆心，大于GH的长为半径作圆弧，两弧在∠ABC内部相交于点O，画射线BO，交AD于点E．连结OG、OH．若∠A＝124°，则∠AEB的大小是___度．【答案】28．【解析】解：由作图可知：∠ABE＝∠CBE，∵AD∥BC，∴∠AEB＝∠CBE，∠A＋∠ABC=180°，∵∠A＝124°，∴∠ABC=56°，∴∠AEB＝∠ABC=＝28°，故答案为：28．14．如图为的角平分线，且，E为延长线上一点，，过E作于F，下列结论：①；②；③；④．其中正确的是________．【答案】①②④【解析】解：①∵BD为△ABC的角平分线，∴∠ABD=∠CBD，又∵BD=BC，BD=BC，∴△ABD≌△EBC（SAS），即①正确；②∵△ABD≌△EBC，∴∠BCE=∠BDA，∴∠BCE+∠BDC=∠BDA+∠BDC=180°，即②正确；③根据已知条件，可得不一定成立，故③错误；④如图，过作于点，是上的点，，在Rt△BEG和Rt△BEF中，，∴Rt△BEG≌Rt△BEF（HL），，在Rt△CEG和Rt△AFE中，，∴Rt△CEG≌Rt△AFE（HL），，，即④正确．故答案为：①②④．15．如图，其中的和是由分别沿着直线，折叠得到的，与相交于点，若，则________°．【答案】80【解析】∵是由沿着直线折叠得到的，∴∠BAE=，∴∠EAC=360°-∠BAE-∵是由沿着直线折叠得到的∴∠E=∠ACB=∠ACD∵∠ACD+∠EAC=+∠E∴∠EAC=80°故答案为：80． 三、解答题16．求证：全等三角形对应边上的中线相等.已知如图，，AD是△ABC的中线．（1）求作的中线（要求尺规作图，不写作法，保留作图痕迹）；（2）求证：【答案】（1）见解析；（2）见解析．【解析】解：（1）如图：即为所求．（2），，∵，分别是与的中线，，，，．17．如图，，直线过点，直线，直线，垂足分别为、，且．（1）求证；（2）求证．【答案】证明见解析．【解析】证明：（1）∵BM⊥直线l，CN⊥直线l，∴∠AMB＝∠CNA＝，在Rt△AMB和Rt△CNA中，，∴Rt△AMB≌Rt△CNA（HL）；（2）由（1）得：Rt△AMB≌Rt△CNA，∴∠BAM＝∠ACN，∵∠CAN+∠ACN＝，∴∠CAN+∠BAM＝，∴∠BAC＝﹣＝18．图，、均为等边三角形，连接、交于点，与交于点．求证：．【答案】证明见解析【解析】证明：∵和都是等边三角形，∴，，，∴，即，在和中，，∴，∴．19．已知：在Rt△ABC中，∠ACB=90°，过点C作CD⊥AB于点D，点E是BC上一点，连接AE交CD于点F.(1)如图1，若AE平分∠CAB，CP平分∠BCD，求证：FP=EP；(2)如图2，若CE=CA，过点E作EG⊥CD于点G，点H为AE的中点，连接DH，GH，判断△GDH的形状，并证明.【答案】(1)证明见解析；(2)△GDH是等腰直角三角形，理由见解析.【解析】(1)∵CD⊥AB，∠ACB=90°，∴∠ACD+∠CAD=90°，∠B+∠CAB=90°，∴∠ACD=∠B，∵AE平分∠CAB，∴∠CAE=∠BAE，∵∠CFE=∠ACD+∠CAE，∠CEF=∠B+∠BAE，∴∠CFE=∠CEF，∴CF=CE，又∵CP平分∠BCD，∴FP=EP； (2)△GDH是等腰直角三角形，理由如下：如图2，延长DH交EG于点M，∵EG⊥CD，∴∠CGE=∠EGD=90°，∴∠CEG+∠ECG=90°，∵∠ACD+∠ECG=∠ACB=90°，∴∠ACD=∠CEG，又∵∠ADC=90°=∠CGE，AC=CE，∴△ACD≌△CEG，∴AD=CG，CD=GE，∵∠ACD=∠B，∴∠CEG=∠B，∴EG//AD，∴∠HAD=∠HEG，∠ADH=∠EMH，又∵AH=EH，∴△ADH≌△EMH，∴EM=AD，DH=MH，∵CD=CG+DG，EG=EM+MG，∴DG=MG，∴△DGM是等腰直角三角形，又∵DH=MH，∴HG⊥DH，GH=DH，∴△GDH是等腰直角三角形.20．如图（1），AB＝4，AC⊥AB，BD⊥AB，AC＝BD＝3．点 P 在线段 AB 上以 1的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动．它们运动的时间为 （s）．（1）若点 Q 的运动速度与点 P 的运动速度相等，当＝1 时，△ACP 与△BPQ 是否全等，请说明理由， 并判断此时线段 PC 和线段 PQ 的位置关系；（2）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变．设点 Q 的运动速度为，是否存在实数，使得△ACP 与△BPQ 全等？若存在，求出相应的、的值；若不存在，请说明理由．【答案】（1）全等，垂直，理由详见解析；（2）存在，或【解析】(1)当t=1时，AP= BQ=1, BP= AC=3,又∠A=∠B= 90°，在△ACP和△BPQ中，∴△ACP≌△BPQ(SAS).∴∠ACP=∠BPQ ,∴∠APC+∠BPQ=∠APC+∠ACP = 90*.∴∠CPQ= 90°，即线段PC与线段PQ垂直；(2)①若△ACP≌△BPQ，则AC= BP，AP= BQ，解得;②若△ACP≌△BQP，则AC= BQ，AP= BP，解得：综上所述,存在或使得△ACP与△BPQ全等.