

2021-2022学年河南省商丘市商丘名校高二下学期期中联考 数学(文)解析版
展开2021-2022学年河南省商丘市商丘名校高二下学期期中联考
数学(文)
一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 观察下列各式:,,则的个位数字是( )
A. 3 B. 9 C. 7 D. 1
【1题答案】
【答案】B
【解析】
【分析】个位数出现顺序为,且周期为4,即可确定的个位数字.
【详解】由题设,个位数出现顺序为,且周期为4,
所以,即的个位数字与相同.
故选:B
2. 虚数单位的引入,使得数系由实数系扩充到了复数系.下面的结构图中,其中1,2,3三个方框中应依次填入( )
A. 复数、小数、整数 B. 复数、无理数、自然数
C. 复数、无理数、整数 D. 复数、整数、小数
【2题答案】
【答案】C
【解析】
【分析】根据实数和复数的概念,直接判断即可.
【详解】由复数的分类可得:1处填入复数;
由实数的分类可得:2处填入无理数;
由有理数的分类可得:3处填入整数.
故选:C.
3. 已知复数(是虚数单位)在复平面内对应的点位于第三象限,则实数m的取值范围为( )
A. B. C. D.
【3题答案】
【答案】C
【解析】
【分析】根据复数在复平面内对应点的特征得到,解之即可求出结果.
【详解】因为复数在复平面内对应的点位于第三象限,得,解得,所以m的取值范围为.
故选:C.
4. 通过对两个具有线性相关关系的变量x和y,利用两组不同的统计数据建立了模型:①;②.对这两个模型进行了残差分析发现:第①个线性模型比第②个线性模型拟合效果好.若用、,、分别表示模型①与模型②的相关指数与残差平方和,则结论正确的是( )
A. , B. ,
C. , D. ,
【4题答案】
【答案】A
【解析】
【分析】相关指数越大,残差平方和越小,拟合效果越好,据此即可判断.
【详解】用相关指数的值判断模型的拟合效果,越大,说明残差平方和越小,模型的拟合效果越好,∵第①个线性模型比第②个线性模型拟合效果好,∴,.
故选:A.
5. 给出如下“三段论”的推理过程:已知是函数的导函数,如果,那么是函数的极值点,(大前提);因为函数在处的导数值,(小前提);所以是函数的极值点.(结论)则上述推理错误的原因是( )
A. 大前提错误 B. 小前提错误
C. 大前提、小前提都错误 D. 推理形式错误
【5题答案】
【答案】A
【解析】
【分析】利用“三段论”的推理和极值点的定义判断.
【详解】因为对应可导函数,如果,且满足和时,导函数值异号,那么是函数的极值点.
所以大前提:“可导函数,如果,那么是函数的极值点”错误,但推理形式正确.
故选:A.
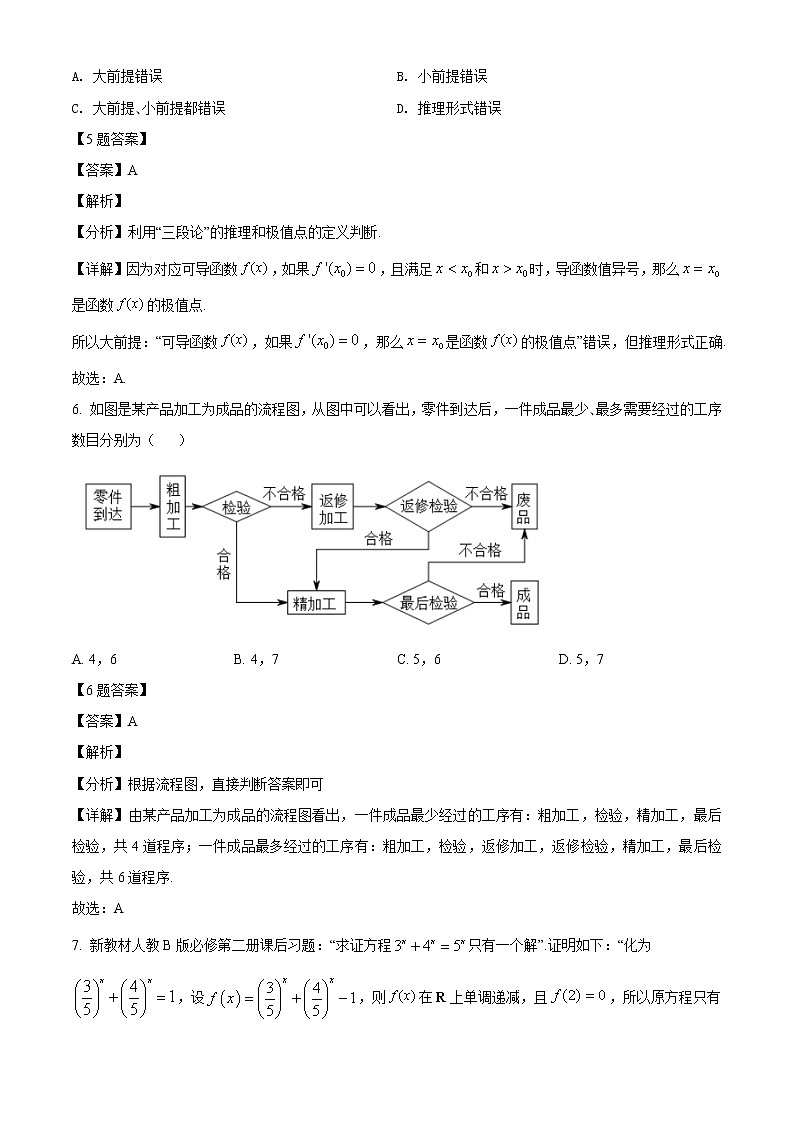
6. 如图是某产品加工为成品的流程图,从图中可以看出,零件到达后,一件成品最少、最多需要经过的工序数目分别为( )
A. 4,6 B. 4,7 C. 5,6 D. 5,7
【6题答案】
【答案】A
【解析】
【分析】根据流程图,直接判断答案即可
【详解】由某产品加工为成品的流程图看出,一件成品最少经过的工序有:粗加工,检验,精加工,最后检验,共4道程序;一件成品最多经过的工序有:粗加工,检验,返修加工,返修检验,精加工,最后检验,共6道程序.
故选:A
7. 新教材人教B版必修第二册课后习题:“求证方程只有一个解”.证明如下:“化为,设,则在R上单调递减,且,所以原方程只有一个解”.类比上述解题思路,解不等式的解集是( )
A. B.
C. D.
【7题答案】
【答案】D
【解析】
【分析】将不等式变形为,进而构造函数,结合函数单调性解不等式即可求出结果.
【详解】由不等式得.设函数,则,由,所以在R上单调递增,所以得,解得或.
故选:D.
8. 已知复数,,且有,,则( )
A. B. C. D.
【8题答案】
【答案】C
【解析】
【分析】根据,,求得,,再由求解.
【详解】因为,,
则,,
因为,
则,
解得,此时,
所以.
故选:C.
9. 甲、乙、丙三人共同收看第24届冬奥会某项目的决赛,他们了解到该项目的参赛运动员来自丹麦、瑞典、挪威、芬兰、冰岛这五个北欧国家,三人做了一个猜运动员国籍的游戏.他们选定了某位运动员,甲说:此运动员来自丹麦或挪威;乙说:此运动员一定不是瑞典和挪威的;丙说:此运动员来自芬兰或冰岛.最后证实,甲、乙、丙三人之中有且只有一人的猜测是正确的,则此运动员来自( )
A. 丹麦 B. 挪威 C. 芬兰 D. 冰岛
【9题答案】
【答案】B
【解析】
【分析】根据题意,逐一分析此运动员来着丹麦、瑞典、挪威、芬兰、冰岛,结合题意,分析即可得答案.
【详解】①若此运动员来自丹麦,则甲、乙、丙三人中甲、乙猜测正确,与题设矛盾,故此运动员不来自丹麦;
②若此运动员来自瑞典,则甲、乙、丙三人都猜测错误,与题设矛盾,故此运动员不来自瑞典;
③若此运动员来自挪威,则甲、乙、丙三人中只有甲猜测正确,与题设相符,故此运动员来自挪威;
④若此运动员来自芬兰,则甲、乙、丙三人中乙、丙猜测是正确,与题设矛盾,故此运动员不来自芬兰;
⑤若此运动员来自冰岛,则甲、乙、丙三人中乙、丙猜测正确,与题设矛盾,故此运动员不来自冰岛.
综上可知,此运动员只能是来自挪威.
故选:B
10. 有如下四个命题,其中正确命题的序号是( )
①在回归直线方程中,当解释变量x每增加一个单位时,预报变量平均增加0.8个单位;
②在线性回归模型中,相关指数表示解释变量x对于预报变量y的贡献率,越接近于0,表示回归效果越好;
③已知X,Y是两个分类变量,若它们的随机变量的观测值k越小,则“X与Y有关系”的把握程度越小;
④在一组样本数据(,),(,),…,(,),(,,,…,不全相等)的散点图中,若所有样本点都在直线上,则这组样本数据的线性相关系数为.
A. ①③ B. ①② C. ②③ D. ①③④
【10题答案】
【答案】A
【解析】
【分析】根据线性回归的相关概念,解析回归方程的意义,逐个选项进行判断即可.
【详解】对于①,在回归直线方程中,当解释变量x每增加一个单位时,预报变量平均增加0.8个单位,①正确;
对于②,在线性回归模型中,相关指数R2表示解释变量x对于预报变量y的贡献率,R2越接近于1,表示回归效果越好,故②错误;
对于③,对分类变量X与Y,对它们的随机变量K2的观测值k来说,k越小,则“X与Y有关系”的把握程度越小,故③正确;
对于④,相关系数反映是两变量之间线性相关程度的强弱,与回归直线斜率无关,题中样本数据的线性相关系数为,故④错误.
故选:A
11. 某实验室在对细胞分裂的研究过程中发现,某种细胞的分裂速度y与细胞所处的温度x的关系可以用模型(其中e为自然对数的底数)进行拟合.设,其变换后得到一组数据:
x | 21 | 23 | 25 | 27 | 29 |
z | 2 | 2.4 | 3 | 3 | 4.6 |
由上表可得线性回归方程为,则当时,估计该细胞的分裂速度y的值为( )
A. 4.9 B. C. 5.9 D.
【11题答案】
【答案】D
【解析】
【分析】由回归直线过样本中心可得,进而代入自变量求估计值.
【详解】由表格数据得:,
,
代入,得:,
所以,即,
从而有,当时,.
故选:D.
12. 随着“双减”政策的逐步落实,其中增加中学生体育锻炼时间的政策引发社会的广泛关注,某教育时报就“支持增加中学生体育锻炼时间的政策是否与性别有关”对某校高二年级部分学生作了专题调查,被调查的男、女生人数相同,其中男生支持的人数占调查男生人数的,女生支持的人数占女生调查人数的.若有99%的把握认为“支持增加中学生体育锻炼时间的政策与性别有关”,则参加调查的学生中男生人数可能为( )
附表:
0.100 | 0.050 | 0.010 | 0.005 | 0.001 | |
2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
附:.
A. 135 B. 145 C. 146 D. 150
【12题答案】
【答案】D
【解析】
【分析】设参加调查的男生、女生各x人,然后完善列联表数据,计算出对比临界值,结合,且x是15的整数倍即可求出结果.
【详解】设参加调查的男生、女生各x人,依题意填写22列联表,如下:
| 支持 | 不支持 | 总计 |
男生 | |||
女生 | |||
总计 |
若有99%的把握认为是否支持该政策与性别有关,则,
即,解得,由题意知,且x是15的整数倍,所以x取150.
故选:D.
二、填空题(本大题共4小题,每小题5分,共20分)
13. 某高中建立了本校女学生的身高和预报体重的回归方程为:,其中,的单位分别是,,则此方程在样本处的残差的绝对值是___________.
【13题答案】
【答案】1.5
【解析】
【分析】利用回归直线方程,求出的估计值,然后求解残差的绝对值.
【详解】由样本数据得到,女大学生的身高预报体重的回归方程是,当时,,此方程在样本处残差的绝对值:.
故答案为:1.5.
14. 若复数,为虚数单位)的实部和虚部相等,则___________.
【14题答案】
【答案】
【解析】
【分析】化简可得,进而得到,再计算模长即可
详解】依题意,,则,得,所以,所以.
故答案为:.
15. 执行如图所示的程序框图,若输出的a的值为33,则输入的整数t的最大值为___________.
【15题答案】
【答案】32
【解析】
【分析】利用程序框图的功能一一循环,直至终止循环求解.
【详解】第一次循环,,不成立;
第二次循环,,不成立;
第三次循环,,不成立;
第四次循环,,,不成立;
第五次循环,,,成立;
所以,
则输入的整数t的最大值为32.
故答案为:32.
16. 在样本点的散点图中,所有的点都在曲线附近波动.经计算,,,则实数b的值为___________.
【16题答案】
【答案】
【解析】
【分析】根据样本中心点满足线性回归方程,代入计算即可
【详解】令,则为,
,,
因为样本中心点在回归直线上,所以,可得.
故答案为:.
三、解答题(共70分.解答应写出文字说明,证明过程或验算步骤)
17. 请选择适当方法证明.
(1)已知,,且,证明:;
(2)已知,,,证明:a,b中至少有一个不小于0.
【17题答案】
【答案】(1)证明见解析
(2)证明见解析
【解析】
【分析】(1)方法一:利用做差法,对因式分解,判断正负即可得出结论;即可证明;方法二:利用综合法即可证明;
(2)结合反正法假设a、b都小于0,推出矛盾即可得出结论.
【小问1详解】
方法一(做差法):
因为,
,
因为且,,所以,
所以,得证
方法二(综合法):因为,,且,
所以,,所以,
展开得:,
所以,
即,得证
【小问2详解】
(反证法)假设a、b都小于0,即,,则有,
因为,,,
则,
这与假设所得相矛盾,因此,假设不成立.
所以,a、b中至少有一个不小于0.
19. 已知复数,,,为虚数单位.
(1)若是纯虚数,求实数m的值;
(2)若,求实数m的值.
【19题答案】
【答案】(1)
(2)
【解析】
【分析】(1)分别化简,然后计算,根据纯虚数的概念即可求解.
(2)因为虚数无法比较大小,所以,由题意可知,为实数,令的实部大于0,虚部为0,即可求解.
【小问1详解】
化简,,
,
因为为纯虚数,
则,解得
【小问2详解】
因为,
则,解得.
21. 开普勒说:“我珍视类比胜过任何别的东西,它是我最可信赖的老师,它能揭示自然界的秘密.”波利亚也曾说过:“类比是一个伟大的引路人,求解立体几何问题往往有赖于平面几何中的类比问题.”在教材选修1—2第二章《推理与证明》的学习中,我们知道,很多平面图形可以推广为空间图形.如正三角形可以推广到正四面体,圆可以推广到球,平行四边形可以推广到平行六面体等.如图1,在三角形ABC中,已知,若,则.类比该命题:
(1)如图2,三棱锥A—BCD中,已知平面ABC,若A点在三角形BCD所在的平面内的射影为M,你能得出什么结论;
(2)判断该命题的真假,并证明.
【21题答案】
【答案】(1)答案见解析;
(2)真命题,证明见解析.
【解析】
【分析】(1)利用类比推理可得命题;
(2)利用线面垂直的判定定理及性质可得,,进而可得,然后利用面积公式即得.
【小问1详解】
命题是:在三棱锥中,已知平面ABC,若A点在三角形BCD所在的平面内的射影为M,则有;
【小问2详解】
该命题为真命题.
证明如下:
连接DM并延长交BC于点E,连接AE,
因为平面ABC,AE、平面ABC,
所以,.
因为平面BCD,DE、平面BCD,
所以,.
因为,
所以平面ADE.
因为AE、平面ADE,
所以,,
因为,,
所以,,
所以,,
所以,,
即.
23. 2022年年度大剧《人世间》自1月28日在央视一套黄金档开播以来,其收视率一路开挂.某调研机构为了解某社区居民对该剧的收视情况,随机抽取了该社区年龄在30~60岁的600名居民进行调查,经统计,其中男性居民与女性居民的人数之比是.收看本剧的居民比没有收看本剧的居民多300人,女性居民中仅有60人没有收看本剧.
(1)完成列联表,并判断是否有99.9%的把握认为收看过电视剧《人世间》与性别有关?
| 观看过 | 没有观看过 | 合计 |
男性 |
|
|
|
女性 |
| 60 |
|
合计 |
|
| 600 |
(2)按性别用分层抽样的方法从收看过本剧的居民中抽取5人,若要从这5人中随机选出2人对其做进一步的观剧感受访谈,求选出的2人中至少有一位是男性居民的概率.
附:,其中.
0.100 | 0.050 | 0.025 | 0.010 | 0.001 | |
2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【23题答案】
【答案】(1)列联表答案见解析,有99.9%的把握认为收看过电视剧《人世间》与性别有关
(2)
【解析】
【分析】(1)根据题目信息完善列联表数据,进而计算出,对比临界值即可得出结论;
(2)根据古典概型的计算公式即可求出结果.
【小问1详解】
由题意,调查的600名居民中,男性与女性居民的人数之比是9:11,故男性有人,女性有人.
因为收看过本剧的居民比没有收看过的居民多300人,所以收看过本剧的居民有450人,
没有收看过本剧的居民有150人;
因为没有收看过本剧的女性有60人,所以收看过本剧的女性居民有270人,没收看过本剧的男性有90人.完成22列联表,如下:
| 观看过 | 没有观看过 | 合计 |
男性 | 180 | 90 | 270 |
女性 | 270 | 60 | 330 |
合计 | 450 | 150 | 600 |
所以,
所以有99.9%的把握认为收看过电视剧《人世间》与性别有关.
【小问2详解】
收看过电视剧《人世间》的共有450人,从中抽取5人,抽到的男性人数、女性人数分别为:(人),(人),
记2名男性分别是a,b;3名女性分别是A,B,C.
则从5人中选出2人的基本事件是:ab,aA,aB,aC,bA,bB,bC,AB,AC,BC,
共10个;选出的2人中至少有一位是男性的事件有7个.
所以选出的2人至少有一位是男性的概率.
25. 应对严重威胁人类生存与发展的气候变化,其关键在于“控碳”,其必由之路是先实现“碳达峰”,而后实现“碳中和”,2020年第七十五届联合国大会上,我国向世界郑重承诺:力争在2030年前实现“碳达峰”,努力争取在2060年前实现“碳中和”,近年来,国家积极发展新能源汽车,某品牌的新能源汽车某区域销售在2021年11月至2022年3月这5个月的销售量y(单位:百辆)的数据如下表:
月份 | 2021年11月 | 2021年12月 | 2022年1月 | 2022年2月 | 2022年3月 |
月份代码:x | 1 | 2 | 3 | 4 | 5 |
销售量y(单位:百辆) | 45 | 56 | 64 | 68 | 72 |
(1)依据表中的统计数据,请判断月份代码x与该品牌的新能源汽车区域销售量y(单位;百辆)是否具有较高的线性相关程度?(参考:若,则线性相关程度一般,若,则线性相关程度较高,计算r时精确度为0.01.)
(2)求销售量y与月份代码x之间的线性回归方程,并预测2022年4月份该区域的销售量(单位:百辆).
参考数据:,,,参考公式:相关系数,线性回归方程中,,,其中,为样本平均值.
【25题答案】
【答案】(1)有较高的线性相关程度
(2),80.8百辆
【解析】
【分析】(1)根据所给数据算出相关系数即可;
(2)根据所给数据和公式算出答案即可.
【小问1详解】
由表中数据可得,,
所以,又,,
所以.
所以月份代码x与销售量y(单位:百辆)具有较高的线性相关程度,可用线性回归模型拟合销售量y与月份代码x之间的关系.
【小问2详解】
由表中数据可得,
则,所以,
令,可得(百辆),
故可预测2022年4月该品牌新能源汽车该区域的销售量为80.8百辆.
27. 椭圆与双曲线之间有许多优美的对称性质,已知椭圆和双曲线
(1)设AB是双曲线的不平行于对称轴且不过原点的弦,M为弦AB的中点,O为坐标原点,则为定值.类比双曲线的性质:若AB是椭圆的不平行于对称轴且不过原点的弦,M为AB的中点,O为坐标原点,试猜想的值,并证明;
(2)设椭圆交x轴于A,B两点,点P是椭圆上异于A,B的任意一点,直线PA,PB分别交y轴于点M,N,则为定值,类比椭圆的性质:若双曲线交x轴于A,B两点,点P是双曲线上异于A,B的任意一点,直线PA,PB分别交y轴于点M,N,试猜想的值,并证明.
【27题答案】
【答案】(1)猜想:,证明见解析
(2)猜想:,证明见解析
【解析】
【分析】(1)设,,,再表示,最后根据A,B满足椭圆的方程式化简即可
(2)设,再根据,求得直线PA方程为,得到点M坐标,表达出,同理得到,再根据满足双曲线方程代入化简即可
【小问1详解】
猜想:.
证明:设,,,则有
,,
则.
将A,B的坐标代入椭圆方程中得:①,②,
①-②得:,,即.
【小问2详解】
猜想:
证明:由题意得,,设,则,
所以直线PA方程为.
令,则,所以点M坐标为.
又,所以;同理可得:.
所以,又因为,
所以,得证.
【点睛】本题主要考查了利用圆锥曲线上的点满足圆锥曲线的方程,进而化简所求表达式的值的方法,需要根据题意根据相关直线的方程联立求解得出相关点的坐标,再化简求解,属于中档题
2023-2024学年河南省商丘市名校联考高二(上)期中数学试卷(含解析): 这是一份2023-2024学年河南省商丘市名校联考高二(上)期中数学试卷(含解析),共19页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
河南省商丘市商丘名校2023-2024学年高一数学上学期期中联考试题(Word版附解析): 这是一份河南省商丘市商丘名校2023-2024学年高一数学上学期期中联考试题(Word版附解析),共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年河南省商丘市五校高二下学期5月联考数学试题(解析版): 这是一份2021-2022学年河南省商丘市五校高二下学期5月联考数学试题(解析版),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












