人教A版 (2019)必修 第二册第十章 概率10.1 随机事件与概率教案配套ppt课件

这是一份人教A版 (2019)必修 第二册第十章 概率10.1 随机事件与概率教案配套ppt课件，共26页。PPT课件主要包含了1包含关系，事件的关系和运算，2相等关系，5互斥事件，6互为对立事件，概率的基本性质，概率的加法公式，不互斥，互斥不对立，互斥且对立等内容，欢迎下载使用。

C1 ={出现1点}；C2={出现2点}； C3={出现3点}； C4 ={出现4点}；C5={出现5点}； C6={出现6点}；
上述事件中有必然事件或不可能事件吗？有的话，哪些是？
D1={出现的点数不大于1}； D2={出现的点数大于3}；D3={出现的点数小于5}； E={出现的点数小于7}; F={出现的点数大于6}; G={出现的点数为偶数}; H={出现的点数为奇数};……
2. 若事件C1发生，则还有哪些事件也一定会发生？反过来可以吗？
3.上述事件中，哪些事件发生会使得 K={出现1点或5点}也发生？
4.上述事件中，哪些事件发生当且仅当事件D2且事件D3同时发生?
5.若只掷一次骰子，则事件C1和事件C2有可能同时发生么？
6.在掷骰子实验中事件G和事件H是否一定有一个会发生？
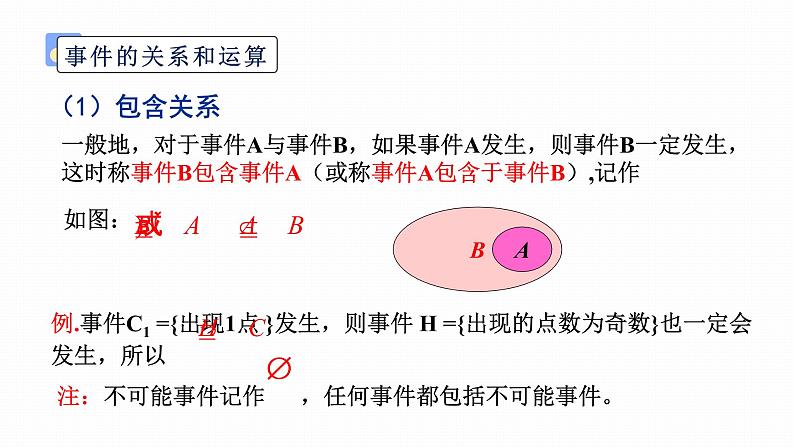
一般地，对于事件A与事件B，如果事件A发生，则事件B一定发生，这时称事件B包含事件A（或称事件A包含于事件B）,记作
例.事件C1={出现1点}发生，则事件D1={出现的点数不大于1}就一定会发生，反过来也一样，所以C1=D1。
（3）并事件（和事件）
若某事件发生当且仅当事件A发生或事件B发生，则称此事件为事件A和事件B的并事件（或和事件），记作 。
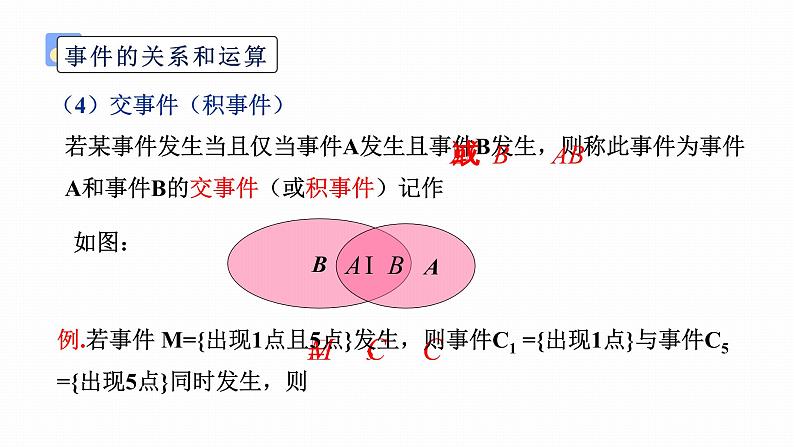
（4）交事件（积事件）
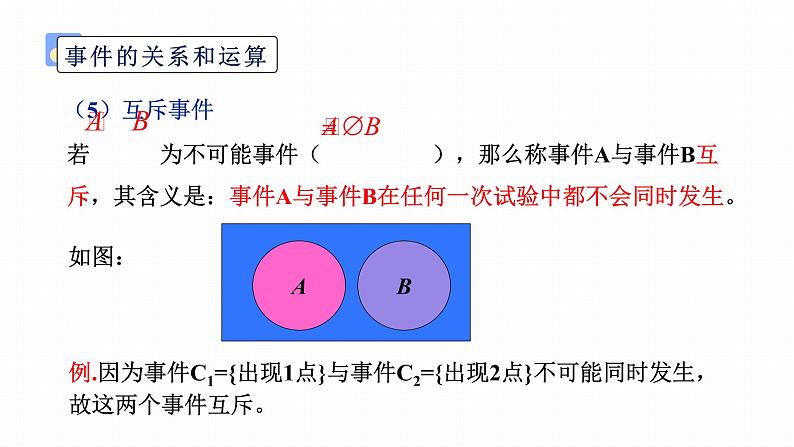
例.因为事件C1={出现1点}与事件C2={出现2点}不可能同时发生，故这两个事件互斥。
例. 事件G ={出现的点数为偶数}与事件H ={出现的点数为奇数} 即为互为对立事件。
①互斥事件可以是两个或两个以上事件的关系，而对立事件只针对两个事件而言。
②从定义上看，两个互斥事件有可能都不发生，也可能有一个发生，也就是不可能同时发生；而对立事件除了要求这两个事件不同时发生外，还要求这二者之间必须要有一个发生，因此，对立事件是互斥事件，是互斥事件的特殊情况，但互斥事件不一定是对立事件。
互斥事件与对立事件的区别：
1.概率P(A)的取值范围
（1）0≤P(A)≤1.
（2）必然事件的概率是1.
（3）不可能事件的概率是0.
结论：当事件A与事件B互斥时
若事件A，B为对立事件，则P(B)=1－P(A)
3.对立事件的概率公式
注意：1.利用上述公式求概率是，首先要确定两事件是否互斥，如果没有这一条件，该公式不能运用。即当两事件不互斥时，应有：
2.上述公式可推广，即如果随机事件A1，A2，……，An中任何两个都是互斥事件，那么有
(1),(3)为互斥事件
1.判断下列每对事件是否为互斥事件
(1)将一枚硬币抛掷两次，事件A：两次出现正面，事件B：只有一次出现正面．(2)某人射击一次，事件A：中靶，事件B：射中9环．(3)某人射击一次，事件A：射中环数大于5，事件B：射中环数小于5.
2.某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛．判断下列每对事件是不是互斥事件，如果是，再判别它们是不是对立事件．(1)恰有一名男生与恰有2名男生；(2)至少有1名男生与全是男生；(3)至少有1名男生与全是女生；(4)至少有1名男生与至少有1名女生．
3.袋中装有白球3个，黑球4个，从中任取3个，是对立事件的为( )①恰有1个白球和全是白球；②至少有1个白球和全是黑球；③至少有1个白球和至少有2个白球；④至少有1个白球和至少有1个黑球． A．① B．②　　C．③　 D．④
4.从一批产品中取出三件产品，设A＝｛三件产品全不是次品｝B＝｛三件产品全是次品｝C＝｛三件产品不全是次品｝则下列结论正确的是（ ）A.只有A和C互斥 B.只有B与C互斥C.任何两个均互斥 D.任何两个均不互斥
5.从装有两个红球和两个黑球的口袋里任取两个球，那么，互斥而不对立的两个事件是（ ）A.至少有一个黑球与都是黑球B.至少有一个黑球与至少有一个红球C.恰好有一个黑球与恰好有两个黑球D.至少有一个黑球与都是红球
6．甲、乙两人下象棋，甲获胜的概率为30%，两人下成和棋的概率为50%，则乙获胜的概率为________，甲不输的概率为________．
7.某射手射击一次射中，10环、9环、8环、7环的概率分别是0.24、0.28、0.19、 0.16，计算这名射手射击一次1）射中10环或9环的概率；2）至少射中7环的概率.3）射中环数不足8环的概率.
(二)根据题意列清各事件后再求解，完成后自由发言.
8.在一次数学考试中，小明的成绩在90分以上的概率是0.13，在80～89分以内的概率是0.55，在70～79分以内的概率是0.16，在60～69分以内的概率是0.12，求小明成绩在60分以上的概率和小明成绩不及格的概率．
[解析]　分别记小明成绩在90分以上，在80～89分，在70～79分，在60～69分，60分以下(不及格)为事件A、B、C、D、E，显然它们彼此互斥，故小明成绩在80分以上的概率为P(A∪B)＝P(A)＋P(B)＝0.13＋0.55＝0.68. 小明成绩在60分以上的概率为P(A∪B∪C∪D)＝P(A)＋P(B)＋P(C)＋P(D)＝0.13＋0.55＋0.16＋0.12＝0.96.∴小明成绩不及格的概率为P(E)＝1－P(A∪B∪C∪D)＝1－0.96＝0.04.
9.一盒中装有各色球12只，其中5红、4黑、2白、1绿，从中取1球．求：(1)取出球的颜色是红或黑的概率；(2)取出球的颜色是红或黑或白的概率．
三.迁移运用，巩固提高
1.事件的关系与运算，区分互斥事件与对立事件