




北京市丰台区2020-2021学年八年级下学期期末数学试卷+解析(试卷+解析)
展开2020-2021学年北京市丰台区八年级(下)期末数学试卷
一、选择题(本题共30分,每小题3分)第1-10题均有四个选项,符合题意的选项只有一个.
1. 函数中自变量的取值范围是( )
A. B. C. D.
2. 下列多边形中,内角和为360°的图形是( )
A. B. C. D.
3. 如图,一束平行光线中,插入一张对边平行纸版,如果光线与纸版右下方所成的∠1是110°,那么光线与纸版左上方所成的∠2的度数是( )
A. 110° B. 100° C. 90° D. 70°
4. 下列运算正确是( )
A. B. C. D.
5. 如图,为了测量一块不规则绿地B,C两点间的距离,可以在绿地的一侧选定一点A,然后测量出AB,AC的中点D,E,如果测量出D,E两点间的距离是8m,那么绿地B,C两点间的距离是( )
A. 4m B. 8m C. 16m D. 20m
6. 在菱形ABCD中,对角线AC,BD相交于点O,如果AC=6,BD=8,那么菱形ABCD的面积是( )
A. 6 B. 12 C. 24 D. 48
7. 下列各曲线中,不表示y是x函数的是( )
A. B. C. D.
8. 在中,对角线,相交于点,只需添加一个条件,即可证明是矩形,这个条件可以是( )
A. B. C. D.
9. 如图,直线y=kx+b与x轴的交点的坐标是(﹣3,0),那么关于x的不等式kx+b>0的解集是( )
A. x>﹣3 B. x<﹣3 C. x>0 D. x<0
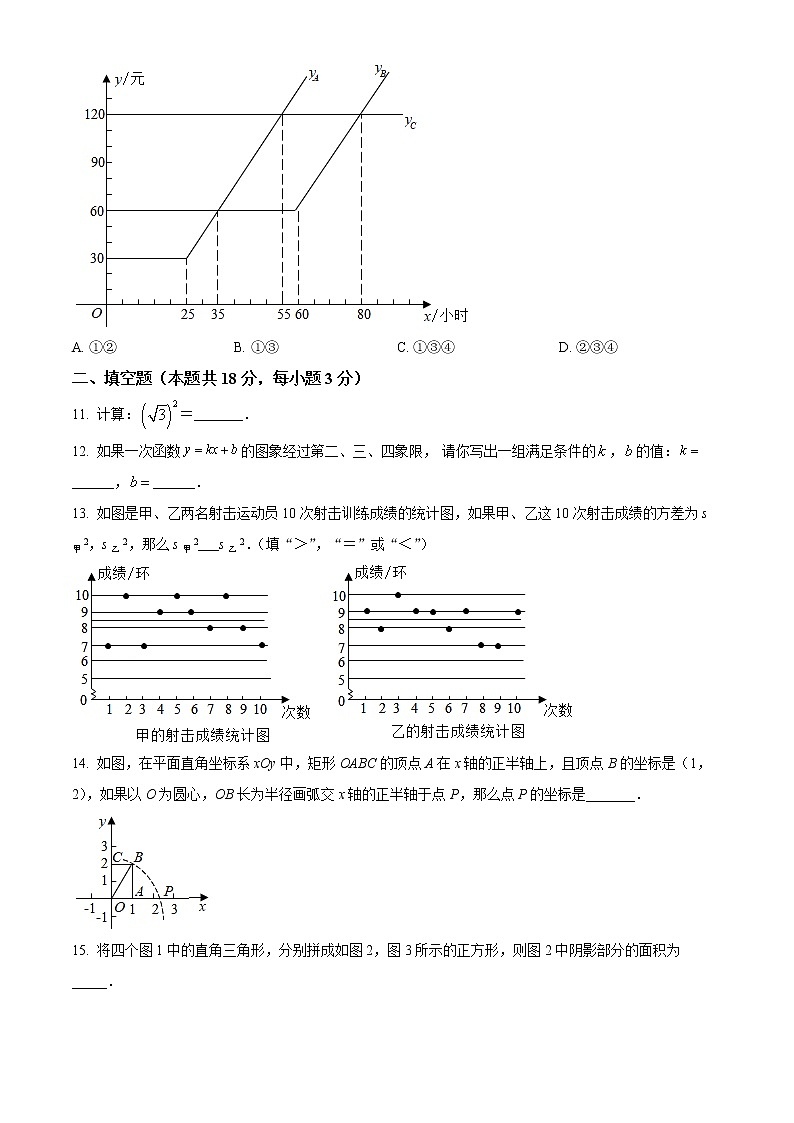
10. A,B,C三种上宽带网方式的月收费金额yA(元),yB(元),yC(元)与月上网时间x(小时)的对应关系如图所示.以下有四个推断:
①月上网时间不足35小时,选择方式A最省钱;
②月上网时间超过55小时且不足80小时,选择方式C最省钱;
③对于上网方式B,若月上网时间在60小时以内,则月收费金额为60元;
④对于上网方式A,若月上网时间超出25小时,则超出的时间每分钟收费0.05元.
所有合理推断的序号是( )
A. ①② B. ①③ C. ①③④ D. ②③④
二、填空题(本题共18分,每小题3分)
11. 计算:=_______.
12. 如果一次函数的图象经过第二、三、四象限, 请你写出一组满足条件的,的值:______,______.
13. 如图是甲、乙两名射击运动员10次射击训练成绩的统计图,如果甲、乙这10次射击成绩的方差为s甲2,s乙2,那么s甲2___s乙2.(填“>”,“=”或“<”)
14. 如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴的正半轴上,且顶点B的坐标是(1,2),如果以O为圆心,OB长为半径画弧交x轴的正半轴于点P,那么点P的坐标是_______.
15. 将四个图1中的直角三角形,分别拼成如图2,图3所示的正方形,则图2中阴影部分的面积为 _____.
16. 如图1,在平面直角坐标系xOy中,□ABCD的面积为10,且边AB在x轴上.如果将直线y=﹣x沿x轴正方向平移,在平移过程中,记该直线在x轴上平移的距离为m,直线被平行四边形的边所截得的线段的长度为n,且n与m的对应关系如图2所示,那么图2中a的值是 ___,b的值是 ___.
三、解答题(本题共52分,第17-20题,每小题5分,第21-23题,每小题5分,第24-25题,每小题5分)
17. 下面是小东设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程.
已知:如图,在Rt△ABC中,∠ABC=90°,O为AC的中点.
求作:四边形ABCD,使得四边形ABCD是矩形.
作法:①作射线BO,以点O为圆心,OB长为半径画弧,交射线BO于点D;
②连接AD,CD.
四边形ABCD是所求作的矩形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵点O为AC的中点,
∴AO=CO.
又∵BO= ,
∴四边形ABCD是平行四边形( )(填推理的依据).
∵∠ABC=90°,
∴□ABCD是矩形( )(填推理的依据).
18. 计算:.
19. 如图,在□ABCD中,E、F分别是AD、BC上的点,且BF=DE.求证:AF=CE.
20. 在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过点A(﹣1,1),B(0,3).
(1)求这个一次函数的解析式;
(2)若这个一次函数的图象与x轴的交点为C,求△BOC的面积.
21. 如图,在△ABC中,∠ACB=90°,D,E分别是边AB,AC的中点,BC=BD,点F在ED的延长线上,且BF//CD.
(1)求证:四边形CBFD为菱形;
(2)连接CF,与BD相交于点O,若CF=4,求AC的长.
22. 某学校在A,B两个校区各有八年级学生200人,为了解这两个校区八年级学生对垃圾分类有关知识的掌握程度,进行了抽样调查,过程如下,请补充完整.
收集数据
从A,B两个校区八年级各随机抽取20名学生,进行了垃圾分类有关知识测试,测试成绩(百分制)如下:
A校区 87 75 79 82 77 76 86 71 76 91
76 80 82 68 73 81 88 69 84 78
B校区 80 73 70 82 71 82 83 93 77 80
81 93 81 73 88 79 81 70 55 83
整理、描述数据
(1)按如下表分数段整理、描述这两组样本数据:
成绩x 人数 校区 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
A | 0 | 2 | 9 | 8 | 1 |
B |
|
| 7 |
| 2 |
(说明:成绩80分及以上为掌握程度优秀,70~79分为掌握程度良好,60~69分为掌握程度合格,60分以下为掌握程度不合格)
分析数据
(2)两组样本数据的平均数、中位数、众数如表所示:
校区 | 平均数 | 中位数 | 众数 |
A | 78.95 |
| 76 |
B | 78.75 | 80.5 |
|
得出结论
①估计B校区八年级对垃圾分类有关知识的掌握程度优秀的学生人数为 ;
②可以推断出 校区的八年级学生对垃圾分类有关知识的掌握程度较好,理由为 .(至少从两个不同的角度说明推断的合理性)
23. 在平面直角坐标系xOy中,直线l1:y=2x+2和直线l2:y=kx+b(k≠0)相交于点A(0,b).
(1)求b的值;
(2)直线l1与x轴交点为B,直线l2与x轴的交点为C,若线段BC的长度大于2,结合函数图象,求k的取值范围.
24. 如图,在正方形ABCD中,点E是边BC上一点(不与点B,C重合),过点C作CF⊥AE,交AE的延长线于点F,过点D作DG⊥FC,交FC的延长线于点G,连接FB,FD.
(1)依题意补全图形;
(2)求∠AFD的度数;
(3)用等式表示线段AF,BF,DF之间的数量关系,并证明.
25. 在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.给出如下定义:如果线段PQ是某个周长为t的矩形的一条对角线,且该矩形的边均与某条坐标轴垂直,那么称点P和点Q互为“t阶矩形点”.如图,点P(1,1)和点Q(3,2)互为“6阶矩形点”.
(1)在点A(1,3),B(2,﹣2),C(3,2)中,与点O互为“8阶矩形点”的点是 ;
(2)若第一象限内有一点N与点O互为“8阶矩形点”,求线段ON长度最小值;
(3)若点M在直线y=x上,且与点M互为“10阶矩形点”的点中恰有2个点与点O互为“8阶矩形点”,记点M的横坐标为m,请直接写出m的取值范围.
2022-2023学年北京市丰台区八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年北京市丰台区八年级(下)期末数学试卷(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年北京市丰台区八年级(上)期末数学试卷: 这是一份2020-2021学年北京市丰台区八年级(上)期末数学试卷
2020-2021学年北京市丰台区九下期末数学试卷: 这是一份2020-2021学年北京市丰台区九下期末数学试卷,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












