



2022年人教版七年级数学下册期末押题卷(三)(原卷+解析)
展开2022年人教版七年级下册期末押题卷(三)
考试时间:120分钟 满分:120分
姓名:__________ 班级:__________考号:__________
题号
一
二
三
总分
评分
一、填空题(共10题;共20分)
1.如图,已知直线a,b被直线c所截,那么∠1的同位角是 ________ .
【答案】 ∠2
【考点】同位角
【解析】【解答】解:∠1的同位角是∠2,故答案为:∠2
【分析】根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角可得答案.
2.不等式组 {x-2≤0x-12
【考点】解一元一次不等式组
【解析】【解答】解: {x-2≤0①x-12
解不等式②得:x>﹣1,
∴不等式组的解集是﹣1<x≤2,
故答案为﹣1<x≤2.
【分析】先求出不等式的解集,再求出不等式组的公共部分。
3.将容量为n的样本中的数据分成6组,绘制频率分布直方图.若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n等于________ .
【答案】 60
【考点】总体、个体、样本、样本容量,频数与频率
【解析】【解答】解:设第一组至第六组数据的频率分别为2x,3x,4x,6x,4x,x,
则2x+3x+4x+6x+4x+x=1,
解得 x=120 ,
所以前三组数据的频率分别是 220,320,420 ,
故前三组数据的频数之和等于 2n20+3n20+4n20 =27,
解得n=60.故答案为60.
【分析】根据题意得到第一组至第六组数据的频率之和是1,得到前三组数据的频率分别是2÷20,3÷20,4÷20;由前三组数据的频数之和等于27,求出样本容量n的值.
4.已知 6x=192 , 32y=192 ,则 [(x-1)(1-y)]2019= ________.
【答案】 -1
【考点】代数式求值,同底数幂的除法,幂的乘方
【解析】【解答】解:∵ 6x =192, 32y =192,,
∴ 6x =192=32×6, 32y =192=32×6,,
∴ 6x-1 =32, 32y-1 =6,,
∴ (6x-1)y-1=6 ,即 6(x-1)(y-1)=6 ,
∴ (x-1)(y-1)=1 ,
∴ [(x-1)(1-y)]2019=[-(x-1)(y-1)]2019=(-1)2019=-1 .
【分析】由 6x =192, 32y =192,推出 6x =192=32×6, 32y =192=32×6,推出 6x-1 =32, 32y-1 =6,可得 (6x-1)y-1=6 ,推出 (x-1)(y-1)=1 ,由此即可解决问题.
5.若一个正数的平方根为2a+1和﹣a﹣3,则a=________,这个正数是________.
【答案】 2;25
【考点】平方根
【解析】【解答】∵一个正数的平方根是2a+1和﹣a﹣3,
∴2a+1﹣a﹣3=0,
解得:a=2,
即这个正数是(2×2+1)2=25,
故答案为:2;25.
【分析】根据正数的两个平方根互为相反数列出方程求出a,再求出这个数的一个平方根,然后平方即可.
6.如果实数x,y满足方程组 {2x-y=1x+y=2 ,那么(-x+2y)2020=________。
【答案】 1
【考点】二元一次方程组的解
【解析】【解答】解: {2x-y=1 ①x+y=2 ② , ②-①得-x+2y=1,∴ (-x+2y)2020=12020=1.
故答案为:1.
【分析】根据等式的性质,由②-①得-x+2y=1,进而整体代入按有理数的乘方运算即可算出答案.
7.《九章算术》是我国古代内容极为丰富的数学名著。书中有下列问题“今有勾八步,股十五步。问勾中容圆径几何?”其意思为今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是________ 步。
【答案】 6
【考点】勾股定理,圆的综合题
【解析】【解答】解:如图所示:
设⊙O内切于△ABC,半径为r,
在Rt△ABC中,AB=8,BC=15,由勾股定理得:
AC=AB2+BC2=17,
根据S∆ABC=12×AB×BC=12×OD×AB+12×BC×OE+12×AC×OF,
可得:8×15=(8+15+17)×r,
解得:r=3,
所以直径d=2r=6
【分析】利用直角三角形三边与内切圆半径的关系求出半径,然后求出直径。
8.若有理数x满足方程|1-x|=1+|x|,则化简|x-1|的结果是________.
【答案】 1−x
【考点】解含绝对值符号的一元一次方程
【解析】【解答】解:①当x≤0时,|1−x|=1−x,1+|x|=1−x,满足题意;
②当0<x<1时,|1−x|=1−x,1+|x|=1+x,不满足题意;
③当x≥1时,|1−x|=x−1,1+|x|=1+x,不满足题意.
综上可得:x≤0,故|x−1|=1−x.
故答案为:1−x.
【分析】根据绝对值的性质,要化简绝对值,可以就x≤0,0<x<1,x≥1三种情况进行分析.
9.若关于x , y的 {a1x+b1y=c1a2x+b2y=c2 的解是 {x=2y=-3 ,则关于m , n的方程组 {2a1(m-n)-3b1(m+n)=5c12a2(m-n)-3b2(m+n)=5c2 的解是________.
【答案】 m=5n=0
【考点】二元一次方程组的解
【解析】【解答】解:由由题意得: {2a1-3b1=c12a2-3b2=c2 ,
∵由 {2a1(m-n)-3b1(m+n)=5c12a2(m-n)-3b2(m+n)=5c2 得 {2a1m-n5-3b1m+n5=c12a2m-n5-3b2m+n5=c2 ,
∴m-n5=1m+n5=1 ,
解得m=5n=0,
故答案为:m=5n=0.
【分析】把 {x=2y=-3 代入原方程得出{2a1-3b1=c12a2-3b2=c2 ,然后把关于m, n的方程组根据这个形式变形,则可得出m-n5=1m+n5=1 , 再解之即可.
10.若不等式3x-m≤0的正整数解恰好是1、2、3,则m的取值范围是________.
【答案】 9≤m<12 .
【考点】解一元一次不等式,一元一次不等式的特殊解,解一元一次不等式组
【解析】【解答】解:∵3x-m≤0 ,
∴ x≤m3 ,
又∵不等式3x-m≤0的正整数解恰好是1、2、3 ,故3≤m3<4 ,
解得 9≤m<12 .
故答案为: 9≤m<12 .
【分析】首先把m,作字母系数解出不等式的解,然后根据不等式3x-m≤0的正整数解恰好是1、2、3 ,得出关于m的不等式组3≤m3<4 ,解不等式组就得出m的取值范围。
二、选择题(共10题;共30分)
11.在下列图形中,∠1与∠2是同位角的是( )
A. B.
C. D.
【答案】 B
【考点】同位角
【解析】【解答】 两条直线a,b被第三条直线c所截(或说a,b相交c),在截线c的同旁,被截两直线a,b的同一侧的角,把这样的两个角称为同位角,B项∠1和∠2符合定义。
A、∠1和∠2不在截线的同旁;故A错误.
B、∠1和∠2在截线的同旁,又在被截两直线的同一侧,故B正确.
C、是内错角,故C错误;
D:、 在截线同旁,但不在被截两直线同侧,故D错误。
故答案为:B
【分析】根据同位角的定义逐项判断。
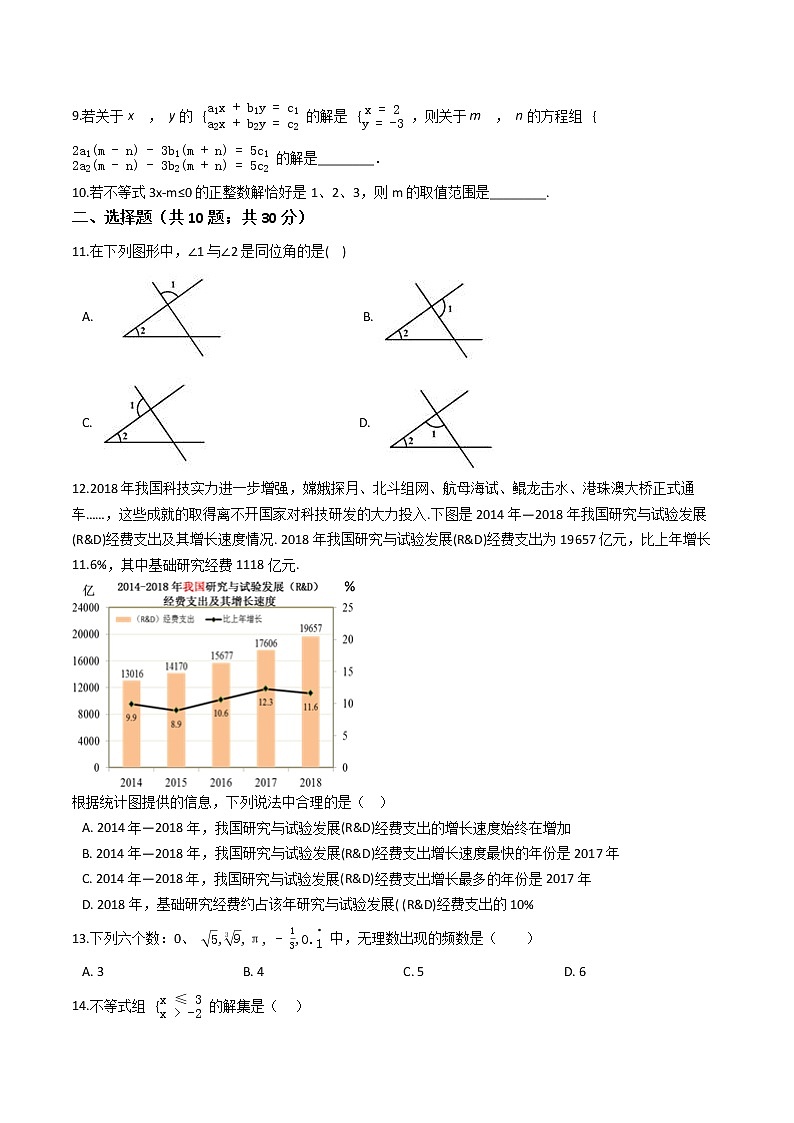
12.2018年我国科技实力进一步增强,嫦娥探月、北斗组网、航母海试、鲲龙击水、港珠澳大桥正式通车……,这些成就的取得离不开国家对科技研发的大力投入.下图是2014年—2018年我国研究与试验发展(R&D)经费支出及其增长速度情况. 2018年我国研究与试验发展(R&D)经费支出为19657亿元,比上年增长11.6%,其中基础研究经费1118亿元.
根据统计图提供的信息,下列说法中合理的是( )
A. 2014年—2018年,我国研究与试验发展(R&D)经费支出的增长速度始终在增加
B. 2014年—2018年,我国研究与试验发展(R&D)经费支出增长速度最快的年份是2017年
C. 2014年—2018年,我国研究与试验发展(R&D)经费支出增长最多的年份是2017年
D. 2018年,基础研究经费约占该年研究与试验发展( (R&D)经费支出的10%
【答案】 B
【考点】条形统计图,折线统计图
【解析】【解答】A. 2014年—2018年,我国研究与试验发展(R&D)经费支出的增长速度在2015年和2018年有所下降,A不符合题意;
B. 2014年—2018年,我国研究与试验发展(R&D)经费支出增长速度最快的年份是2017年,此选项符合题意;
C. 2014年—2018年,我国研究与试验发展(R&D)经费支出增长最多的年份是2018年,C不符合题意;
D. 2018年,基础研究经费约占该年研究与试验发展( (R&D)经费支出的5.7%,故此选项不符合题意.
故答案为:B.
【分析】利用条形统计图和折线统计图结合相应数据,分别分析得出正确的答案.
13.下列六个数:0、 5,39,π,-13,0.1• 中,无理数出现的频数是( )
A. 3 B. 4 C. 5 D. 6
【答案】 A
【考点】频数与频率,无理数的认识
【解析】【解答】因为六个数:0、 5,39,π,-13,0.1• 中,无理数是 5,39,π
即:无理数出现的频数是3
故答案为:A
【分析】根据无理数的定义找出无理数,根据频数的定义可得频数.
14.不等式组 {x≤3x>-2 的解集是( )
A. ﹣2<x≤3 B. ﹣2≤x<3 C. x≥3 D. x<﹣2
【答案】 A
【考点】解一元一次不等式组
【解析】【解答】解:不等式组 {x≤3x>-2 的解集是﹣2<x≤3,
故答案为:A.
【分析】根据找不等式组解集的规律找出即可.
15.已知实数a,b,若a>b,则下列结论错误的是( )
A. a+6>b+6 B. a﹣2>b﹣2 C. ﹣2a>﹣2b D. a3>b3
【答案】 C
【考点】不等式及其性质
【解析】【解答】A.两边都加6,不等号的方向不变,故A不符合题意;
B.两边都减2,不等号的方向不变,故B不符合题意;
C.两边都乘﹣2,不等号的方向改变,故C符合题意;
D.两边都除以3,不等号的方向不变,故D不符合题意.
故答案为:C.
【分析】根据不等式的基本性质,基本加减乘除运算后符号变化,对选项进行判断即可。
16.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于12EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
A. 20° B. 25° C. 30° D. 40°
【答案】 A
【考点】尺规作图的定义
【解析】【解答】解:由题意可得:AH平分∠CAB,
∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠ACD=140°,
∴∠CAB=40°,
∵AH平分∠CAB,
∴∠HAB=20°,
∴∠AHC=20°.
故选A.
【分析】根据题意可得AH平分∠CAB,再根据平行线的性质可得∠CAB的度数,再根据角平分线的性质可得答案.
17.利用科学计算器求值时,小明的按键顺序为 ,则计算器面板显示的结果为( )
A. -2 B. 2 C. ±2 D. 4
【答案】 B
【考点】计算器在数的开方中的应用
【解析】【解答】4的算术平方根 4=2 ,
故答案为:B.
【分析】根据算术平方根的求解方法进行计算即可得解.
18.七年级学生在会议室开会,每排座位坐12人,则有11人没有座位;每排座位坐14人,则余1人独坐一排,则这间会议室的座位排数是( )
A. 14 B. 13 C. 12 D. 15
【答案】 C
【考点】二元一次方程组的其他应用
【解析】【解答】解:设这间会议室的座位排数是x排,人数是y人.
根据题意,得
{12x+11=y14(x-1)+1=y ,
解得
{x=12y=155 .
故答案为:C.
【分析】本题中有两个等量关系:1、每排坐12人,则有11人没有座位;2、每排坐14 人,则余1人独坐一排. 这样设每排的座位数为x ,总人数为y,列出二元一次方程组即可.
19.如图所示,BA⊥AC,AD⊥BC,垂足分别为A,D,已知AB=3,AC=4,BC=5,AD=2.4,则点A到线段BC的距离是( )
A. 2.4 B. 3 C. 4 D. 5
【答案】 A
【考点】点到直线的距离
【解析】【分析】∵AD=2.4,AD⊥BC,
∴点A到线段BC的距离是AD的长,即是2.4,
选A
【点评】难度系数小,关键是理解点到直线的距离定义。
20.在本学期的“献爱心”的捐款活动中,九(1)班学生捐款情况如图,那么捐款金额的众数和中位数分别是( )
A. 15和13.5 B. 8元和6.5元 C. 15和8元 D. 8元和8元
【答案】 B
【考点】条形统计图
【解析】【解答】解:根据条形统计图得到捐8元的学生数最多,为15个,故捐款金额的众数为8元,
将捐款数按照从小到大顺序排列得到3,3,3,3,3,3,3,3,5,5,5,5,5,5,5,5,5,5,5,5,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,10,10,10,10,10,其中最中间的两个数为5和8,平均数为6.5,即中位数为6.5,
故选B
【分析】根据条形统计图中的数据求出众数与中位数即可.
三、解答题(共9题;共70分)
21.解不等式: x+12 ﹣ x-13 ≤1并将其解集在数轴上表示出来.
【答案】 解:去分母得,3(x+1)﹣2(x﹣1)≤6,
去括号得,3x+3﹣2x+2≤6,
移项得,3x﹣2x≤6﹣3﹣2,
合并同类项得,x≤1.
在数轴上表示为:
【考点】解一元一次不等式,在数轴上表示不等式的解集
【解析】【分析】先去分母,再去括号,移项,合并同类项,再在数轴上表示出来即可.
22.甲、乙两位同学共同解方程组 {ax+5y=15①4x-by=-2② ,由于甲同学看错了方程①中的a,得到方程组的解为 {x=-3y=-1 ;乙同学看错了方程②中的b,得到方程组的解为 {x=5y=4 ,现请你根据甲、乙两位同学的解,求出a,b的值,并解出原方程中的x和y.
【答案】解:根据题意得: , 解得:a=﹣1,b=10,
方程组为 ,
①×2+②得:2x=28,即x=14,
把x=14代入①得:y=5.8.
【考点】二元一次方程组的解
【解析】【分析】把甲的结果代入方程②求出b的值,把乙的结果代入方程①求出a的值,确定出方程组,求出解即可.
23.某批服装进价为每件200元,商店标价每件300元,现商店准备将这批服装打折出售,但要保证毛利润不低于 5% ,问售价最低可按标价的几折? ( 要求通过列不等式进行解答 )
【答案】 解:设售价可以按标价打x折,
根据题意,得: 200+200×5%≤300×x10 ,
解得: x≥7 ,
答:售价最低可按标价的7折.
【考点】一元一次不等式的应用
【解析】【分析】设售价可以按标价打x折,根据“保证毛利润不低于 5% ”列出不等式,解之可得.
24.如图,已知∠A=80°,BO,CO分别平分∠ABC,∠ACB,DE经过点O,且DE∥BC,求∠BOC的度数。
【答案】 解:在三角形ABC中
∵∠A+∠ABC+∠ACB=180°
又∵∠A=80°
∴∠ABC+∠ACB=100°
又∵CO、BO分别平分∠ACB,∠ABC
∴∠OCB= 12 ∠ACB,∠OBC= 12 ∠ABC
∴2∠OCB+2∠OBC=100°
∴∠OCB+∠OBC=50°
在三角形OBC中
∵∠OCB+∠OBC+∠BOC=180°
∴∠BOC=180°-(∠OCB+∠OBC)
=180°-50°
=130。
∴∠BOC的度数为130°
【考点】角的运算,平行线的性质,角平分线的定义
【解析】【分析】本题主要利用平行线的性质和角平分线的定义进行求解即可。
25.MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
【答案】 解:延长MF交CD于点H∠1=90∠FH,2140∴∠CHF=1405-902=50°,∠CHF=∠2,AB∥CD
【考点】平行线的判定
【解析】【分析】延长MF交CD于点H,根据已知条件可证得∠CHF=∠2,再根据同位角相等,两直线平行可证明AB∥CD。
26.阅读下面的文字,解答问题:大家知道 2 是无理数,而无理数是无限不循环小数,因此 2 的小数部分我们不可能全部地写出来,于是小明用 2 -1来表示 2 的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为 2 的整数部分是1,将这个数减去其整数部分,差就是小数部分。
又例如:
∵ 4 < 7 < 9 ,即2< 7 <3,
∴ 7 的整数部分为2,小数部分为( 7 -2).
请解答:
(1)17 的整数部分是________,小数部分是________。
(2)如果 5 的小数部分为a, 13 的整数部分为b,求a+b- 5 的值;
(3)已知:10+ 3 =x+y,其中x是整数,且0
(2)解:∵2< <3, ∴a= ﹣2,
∵3< <4,
∴b=3,
∴a+b﹣ = ﹣2+3﹣ =1;
(3)解:∵1<3<4, ∴1< <2,
∴11<10+ <12,
∵10+ =x+y,其中x是整数,且0<y<1,
∴x=11,y=10+ ﹣11= ﹣1,
∴x﹣y=11﹣( ﹣1)=12﹣ ,
∴x﹣y的相反数是﹣12+ ;
【考点】实数的运算
【解析】【分析】(1)根据题意,得出整数部分和小数部分。
(2)根据已知条件,可利用范围,得出结果。
(3)根据已知,进行运算,得出相反数。
27.为鼓励居民节约用电,广州市自2012年以来对家庭用电收费实行阶梯电价,即每月对每户居民的用电量分为三个档级收费,第一档为用电量在180千瓦时(含180千瓦时)以内的部分,执行基本价格;第二档为用电量在180千瓦时到450千瓦时(含450千瓦时)的部分,实行提高电价;第三档为用电量超出450千瓦时的部分,比第二档的单价每千瓦时提高0.05元. 海珠区的李白同学家今年2月份用电330千瓦时,电费为213元,3月份用电240千瓦时,电费为150元.已知我市的另一位居民杜甫家今年4、5月份的家庭用电量分别为200和 490千瓦时,请你依据题目条件,计算杜甫家4、5月份的电费分别为多少元?
【答案】 解:设基本电价为x元/千瓦时,提高电价为y元/千瓦时,
由题意得, {180x+150y=213180x+60y=150 ,
解得: {x=0.6y=0.7 ,
0.7+0.05=0.75元
则四月份电费为:180×0.6+0.7×(200-180)= 122(元),
五月份电费为:180×0.6+(450-180)×0.7+(490-450)×0.75=108+189+30= 327 (元).
答:杜甫家四月份的电费为96元,五月份的电费为269元
【考点】二元一次方程组的其他应用
【解析】【分析】本题属于阶梯性收费问题,电价被分成了三个阶梯,基本价格+第二档的价格+第三档的价格=总价格. 所以要看用电度数属于第几档,李白家2月份用电330千瓦时,属于前两档,所以基础价格+第二档的价格=213;3月份用电240千瓦时,同样属于第二档,所以可以列出二元一次方程组,求出基础电价和第二档的电价;进而求出第三档的电价,再求出杜甫家的用电总费用即可.
2022年人教版七年级数学下册期末押题卷(八)(原卷+解析): 这是一份2022年人教版七年级数学下册期末押题卷(八)(原卷+解析),文件包含2022年人教版七年级数学下册期末押题卷八解析版docx、2022年人教版七年级数学下册期末押题卷八原卷版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
2022年人教版七年级数学下册期末押题卷(七)(原卷+解析): 这是一份2022年人教版七年级数学下册期末押题卷(七)(原卷+解析),文件包含2022年人教版七年级数学下册期末押题卷七解析版docx、2022年人教版七年级数学下册期末押题卷七原卷版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
2022年人教版七年级数学下册期末押题卷(六)(原卷+解析): 这是一份2022年人教版七年级数学下册期末押题卷(六)(原卷+解析),文件包含2022年人教版七年级数学下册期末押题卷六解析版docx、2022年人教版七年级数学下册期末押题卷六原卷版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。












