2023年高考数学(理数)一轮复习课时36《由三视图求几何体面积、体积》达标练习（含详解）

2023年高考数学(理数)一轮复习课时36

《由三视图求几何体面积、体积》达标练习

一 、选择题

1.一个几何体的三视图如图所示(单位：cm)，则该几何体的表面积为(　　)

A.10 cm2      B.cm2        C.cm2        D.(10＋)cm2

2.如下图所示，在三棱锥D－ABC中，已知AC＝BC＝CD＝2，CD⊥平面ABC，∠ACB＝90°.

若其正视图、俯视图如右图所示，则其侧视图的面积为(　　)

A.         B.2           C.         D.

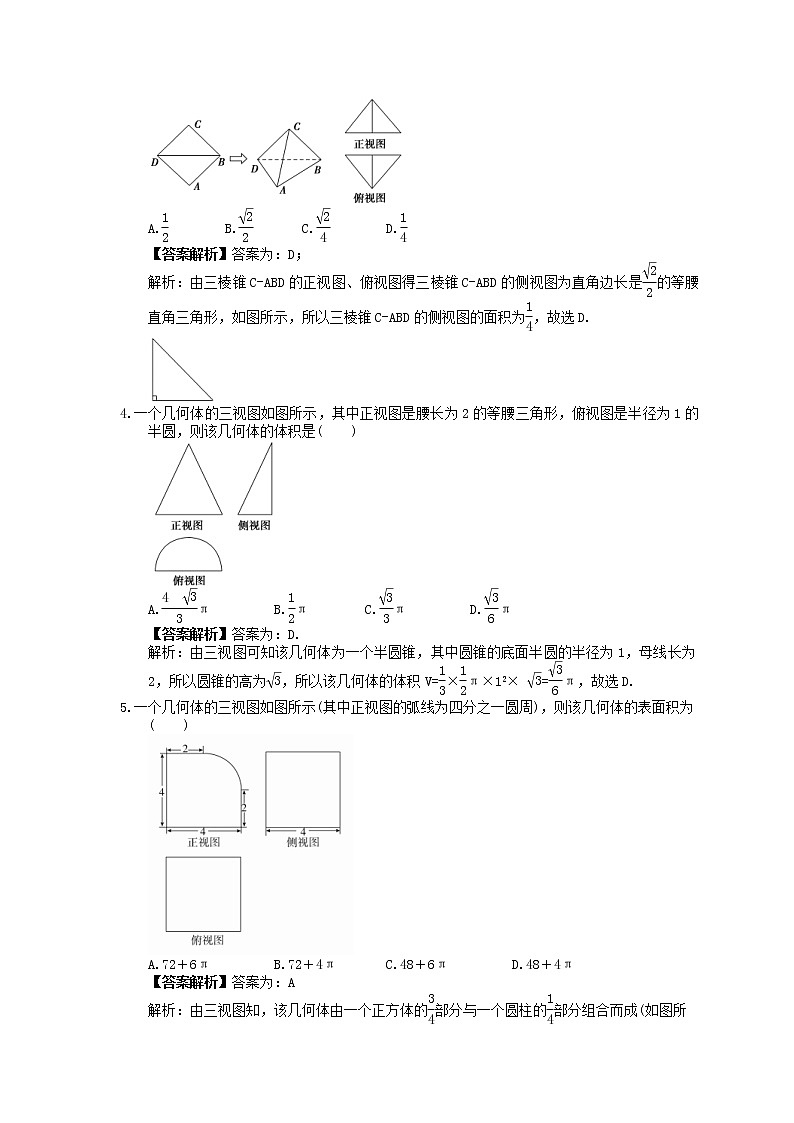
3.把边长为1的正方形ABCD沿对角线BD折起，使得平面ABD⊥平面CBD，形成的三棱锥C-ABD的正视图与俯视图如图所示，则侧视图的面积为(　　)

A.        B.       C.        D.

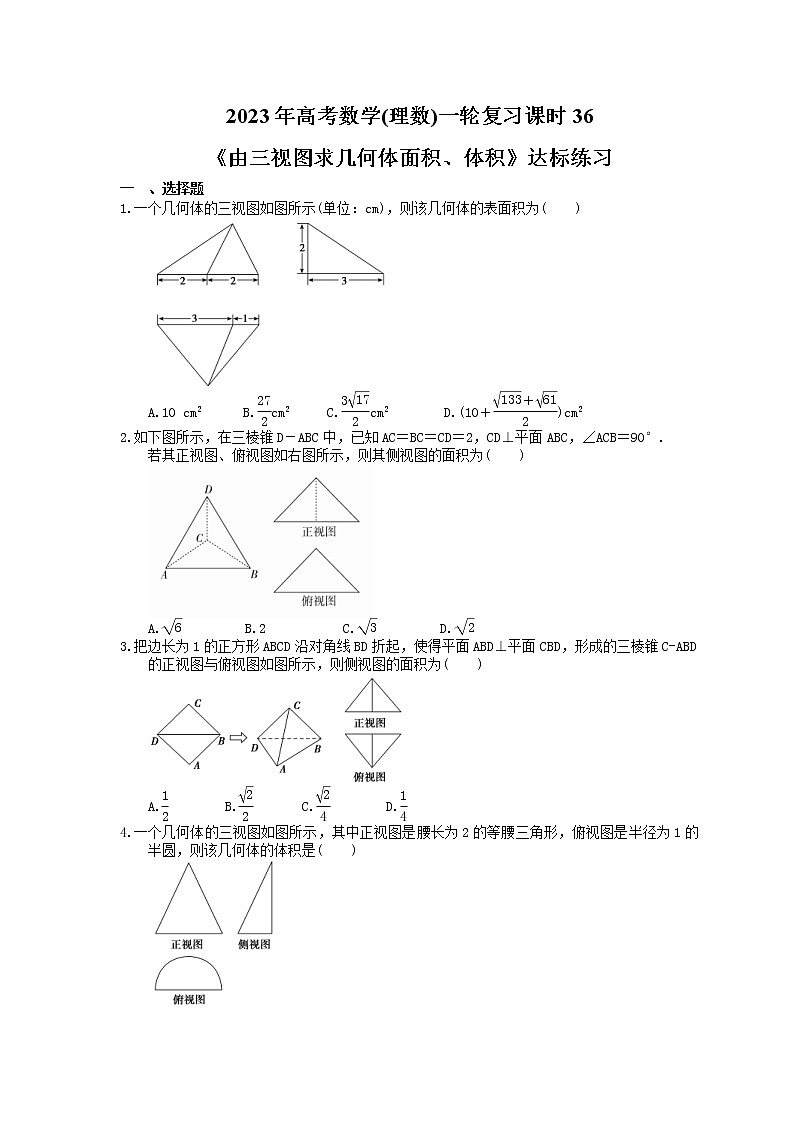
4.一个几何体的三视图如图所示，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是(　　)

A.π         B.π        C.π         D.π

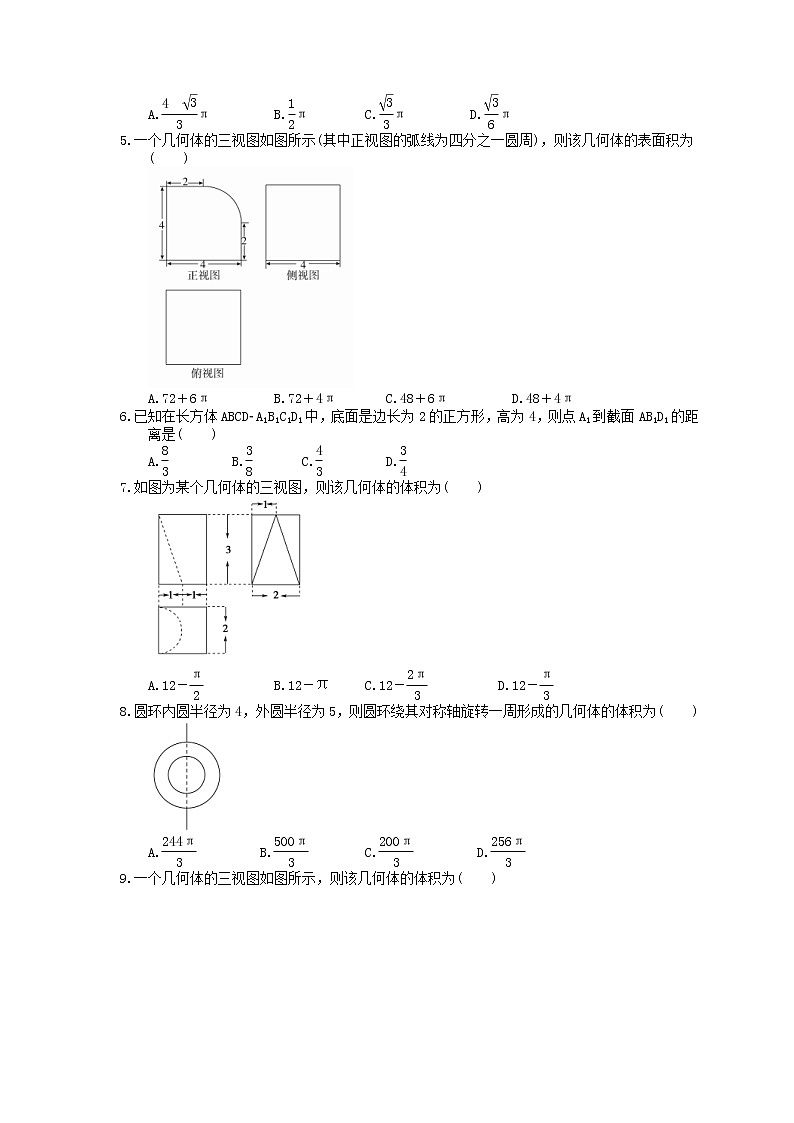
5.一个几何体的三视图如图所示(其中正视图的弧线为四分之一圆周)，则该几何体的表面积为(　　)

A.72＋6π         B.72＋4π       C.48＋6π         D.48＋4π

6.已知在长方体ABCD­A1B1C1D1中，底面是边长为2的正方形，高为4，则点A1到截面AB1D1的距离是(　　)

A.         B.       C.         D.

7.如图为某个几何体的三视图，则该几何体的体积为(　　)

A.12－　　　　　B.12－π     C.12－          D.12－

8.圆环内圆半径为4，外圆半径为5，则圆环绕其对称轴旋转一周形成的几何体的体积为(　　)

A.         B.        C.         D.

9.一个几何体的三视图如图所示，则该几何体的体积为(　　)

A.π        B.         C.　        D.

10.已知四棱锥S­ABCD的所有顶点都在球O的球面上，SD⊥平面ABCD，底面ABCD是等腰梯形，AB∥CD且满足AB=2AD=2DC=2，且∠DAB=，SC=，则球O的表面积是(　　)

A.5π      B.4π                 C.3π      D.2π

11.一锥体的三视图如图所示，则该棱锥的最长棱的棱长为（        ）

A.                         B.                        C.                         D.

12.已知正方体ABCD－A′B′C′D′的外接球的体积为，将正方体割去部分后，剩余几何体的三视图如图所示，则剩余几何体的表面积为(　　)

A.＋         B.3＋或＋       C.2＋        D.＋或2＋

二 、填空题

13.如图，在四棱锥P­ABCD中，底面ABCD是矩形，PD⊥底面ABCD，M，N分别为AB，PC的中点，PD=AD=2，AB=4.则点A到平面PMN的距离为________.

14.某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为2 cm的半圆，虚线是等腰三角形的两腰)，俯视图是一个半径为2 cm的圆(包括圆心)，则该零件的体积是______.

15.已知三棱锥A－BCD中，AB＝AC＝BC＝2，BD＝CD＝，点E是BC的中点，点A在平面BCD内的射影恰好为DE的中点，则该三棱锥外接球的表面积为________.

16.在四棱锥S-ABCD中，AB//CD，，，，

则三棱锥S-ABD外接球的表面积为______.

0.答案解析

1.答案为：D；

解析：由三视图可知，该几何体为三棱锥，其直观图如图所示，其中底面是底边长为4，

高为3的等腰三角形，后侧面是底边长为4，高为2的三角形，左边一个侧面是等腰三角形，还有一个侧面是非特殊三角形，所以表面积S=×4×3＋×4×2＋××

＋×××=10＋(cm2).

2.答案为：D

解析：由几何体的结构特征和正视图、俯视图，得该几何体的侧视图是一个直角三角形，

其中一直角边为CD，其长度为2，另一直角边为底面三角形ABC的边AB上的中线，

其长度为，则其侧视图的面积为S＝×2×＝，故选D.

3.答案为：D；

解析：由三棱锥C-ABD的正视图、俯视图得三棱锥C-ABD的侧视图为直角边长是的等腰直角三角形，如图所示，所以三棱锥C-ABD的侧视图的面积为，故选D.

4.答案为：D.

解析：由三视图可知该几何体为一个半圆锥，其中圆锥的底面半圆的半径为1，母线长为2，所以圆锥的高为，所以该几何体的体积V=×π×12× =π，故选D.

5.答案为：A

解析：由三视图知，该几何体由一个正方体的部分与一个圆柱的部分组合而成(如图所示)，

其表面积为16×2＋(16－4＋π)×2＋4×(2＋2＋π)＝72＋6π.故选A.

6.答案为：C；

解析：设点A1到截面AB1D1的距离是h，由VA1­AB1D1=VA­A1B1D1，

可得S△AB1D1·h=S△A1B1D1·AA1，即××2×2×4=×h，解得h=.

7.答案为：A.

解析：由三视图可知，该几何体是由一个正四棱柱挖掉一个半圆锥所得到的几何体，

其直观图如图所示，

其中正四棱柱的底面正方形的边长a=2，半圆锥的底面半径r=1，高h=3，

所以正四棱柱的体积V1=a2h=22×3=12，半圆锥的体积V2=×r2h=×12×3=，

所以该几何体的体积V=V1－V2=12－.]

8.答案为：A；

解析：该旋转体是大球体中挖掉一个小球体，该旋转体体积为V=×53－×43=.

9.答案为：D

解析：由题图可知该几何体是一个底面圆的半径为1，高为1的半圆锥，

故所求体积V=×π×12×1=.故选答案为：D.

10.答案为：A；

解析：依题意得，AB=2AD=2，∠DAB=，由余弦定理可得BD=，则AD2＋DB2=AB2，

则∠ADB=，又四边形ABCD是等腰梯形，故四边形ABCD的外接圆直径为AB，

设AB的中点为O1，球的半径为R，因为SD⊥平面ABCD，

所以R2=12＋=，则S=4πR2=5π，故选A.

11.【解答】解：由三视图知：几何体是四棱锥，且四棱锥的一个侧面与底面垂直，

底面为边长为4的正方形如图：其中PAD⊥平面ABCD，底面ABCD为正方形，

PE⊥AD，DE=1，AE=3，PE=4，PE⊥底面ABCD，连接CE，BE，

在直角三角形PBE中，PB===；

在直角三角形PCE中，可得PC===；

又PA===5；PD===．

几何体最长棱的棱长为．故选：C．

12.答案为：B

解析：设正方体的棱长为a，依题意得，×＝，解得a＝1.

由三视图可知，该几何体的直观图有以下两种可能，图1对应的几何体的表面积为

＋，图2对应的几何体的表面积为3＋.故选B.

二 、填空题

13.答案为：.

解析：取PD的中点E，连接AE，NE，则在四棱锥P­ABCD中，底面ABCD是矩形，

M，N分别为AB，PC的中点，所以NE∥AM，NE=AM，

所以四边形AENM是平行四边形，所以AE∥MN，

所以点A到平面PMN的距离等于点E到平面PMN的距离，设为h，

在△PMN中，PN=，PM=2，MN=，所以S△PMN=×2×=，

由VE­PMN=VM­PEN，可得×h=××1×2×2，所以h=.

14.答案为：4π cm3

解析：依题意得，零件可视为从一个半球中挖去一个小圆锥所剩余的几何体，

其体积为××23－×π×22×1=4π(cm3).

15.答案为：.

解析：如图，作出三棱锥A－BCD的外接球，设球的半径为r，球心O到底面BCD的距离为d，DE的中点为F，连接AF，过球心O作AF的垂线OH，垂足为H，连接OA，OD，OE，AE.

因为BD＝，CD＝，BC＝2，所以BD⊥CD，则OE⊥平面BCD，OE∥AF，

所以HF＝OE＝d.所以在Rt△BCD中，DE＝1，EF＝.

又AB＝AC＝BC＝2，所以AE＝，所以在Rt△AFE中，AF＝，

所以r2＝d2＋1＝( -d)2＋，解得r2＝，

所以三棱锥A－BCD的外接球的表面积S＝4πr2＝.

16.答案为：

解析：如图所示，取CD的中点，连接，，并连接BD交于，连接SH.

因为，，

所以四边形和四边形均为平行四边形，

所以，故，

所以为外接圆的圆心且，

则，，，

因为，所以，所以.

因为，，所以，所以，

因为，所以平面

设三棱锥外接球的球心为，连接，，，

则平面，则.过点作于点，则，

故四边形为矩形，故，.

设，外接球的半径为，则，

又，则，解得，所以，

所以三棱锥外接球的表面积为.