



所属成套资源:2023年高考数学(理数)一轮复习课时 达标练习(答案版+教师版)
2023年高考数学(理数)一轮复习课时38《空间线、面的平行关系》达标练习(含详解)
展开
这是一份2023年高考数学(理数)一轮复习课时38《空间线、面的平行关系》达标练习(含详解),文件包含2023年高考数学理数一轮复习课时38《空间线面的平行关系》达标练习含详解doc、2023年高考数学理数一轮复习课时38《空间线面的平行关系》达标练习教师版doc等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
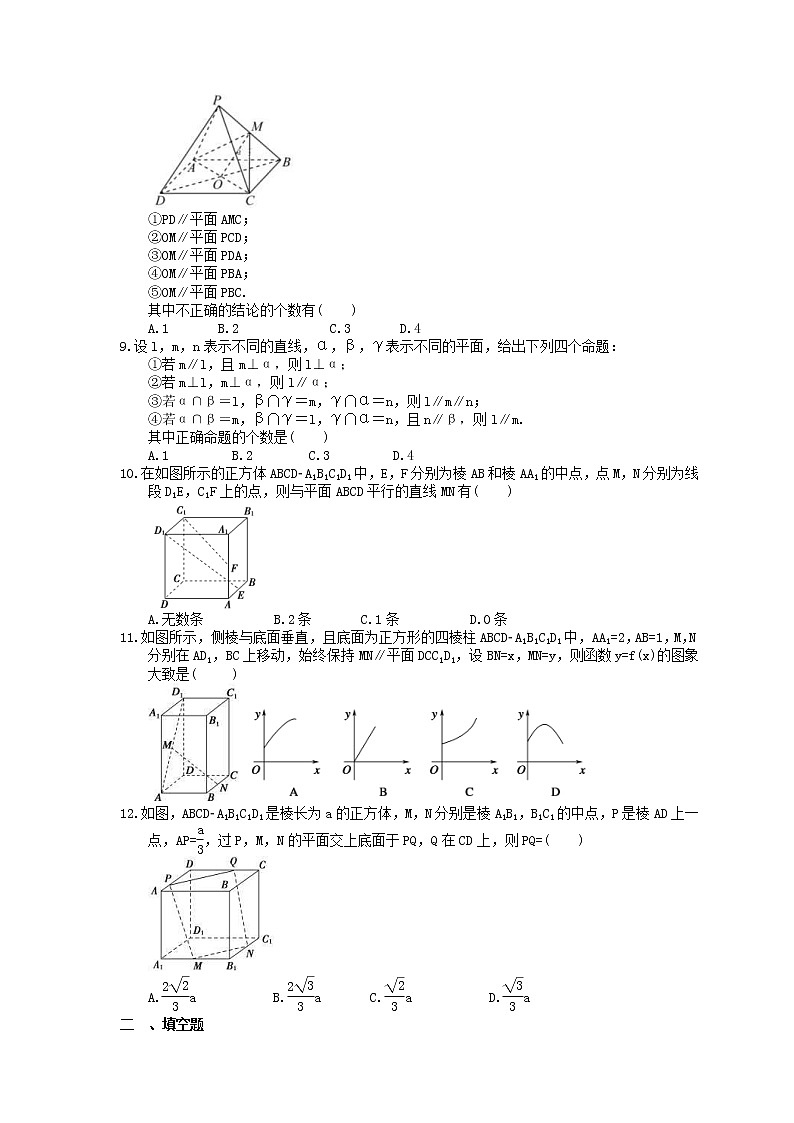
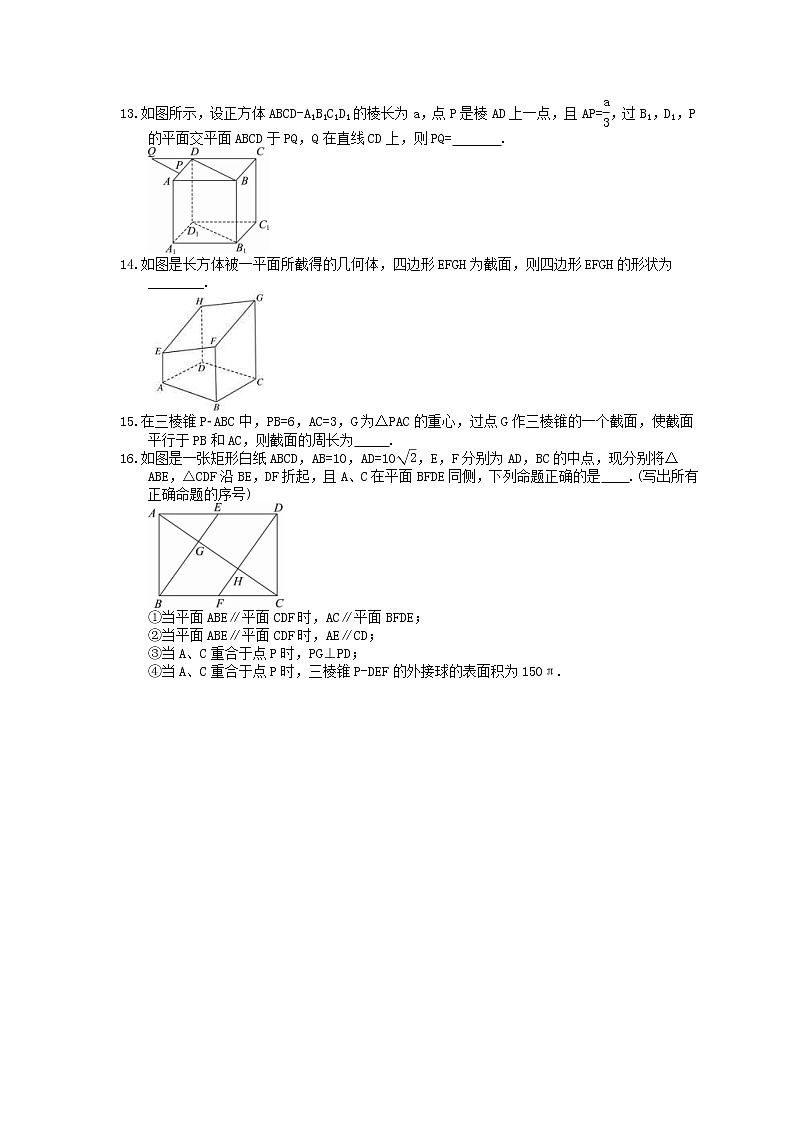
2023年高考数学(理数)一轮复习课时38《空间线、面的平行关系》达标练习一 、选择题1.已知α,β为平面,a,b,c为直线,下列命题正确的是( )A.a⊂α,若b∥a,则b∥αB.α⊥β,α∩β=c,b⊥c,则b⊥βC.a⊥b,b⊥c,则a∥cD.a∩b=A,a⊂α,b⊂α,a∥β,b∥β,则α∥β【答案解析】答案为:D;解析:选项A中,b⊂α或b∥α,不正确.B中b与β可能斜交或b在β内,B错误.C中a∥c,a与c异面,或a与c相交,C错误.利用面面平行的判定定理,易知D正确.2.已知α是一个平面,m,n是两条直线,A是一个点,若m⊄α,n⊂α,且A∈m,A∈α,则m,n的位置关系不可能是( )A.垂直 B.相交 C.异面 D.平行【答案解析】答案为:D.解析:对于选项A,当m⊥α时,因为n⊂α,所以m⊥n,可能;对于选项B,当A∈n时,m∩n=A,可能;对于选项C,若A∉n,由异面直线的定义知m,n异面,可能;对于选项D,若m∥n,因为m⊄α,n⊂α,所以m∥α,这与m∩α=A矛盾,不可能平行,故选D.3.设a,b为两条不同的直线,α,β为两个不同的平面.则下列四个命题中,正确的是( )A.若a,b与α所成的角相等,则a∥bB.若a∥α,b∥β,α∥β,则a∥bC.若a⊂α,b⊂β,a∥b,则α∥βD.若a⊥α,b⊥β,α⊥β,则a⊥b【答案解析】答案为:D;解析:对于选项A,a,b不一定平行,也可能相交;对于选项B,只需找个平面γ,使γ∥α∥β,且a⊂γ,b⊂γ即可满足题设,但a,b不一定平行;对于选项C,由直三棱柱模型可排除C.4.如图,在长方体ABCD-A′B′C′D′中,下列直线与平面AD′C平行的是( )A.B′C′ B.A′B C.A′B′ D.BB′【答案解析】答案为:B解析:连接A′B,∵A′B∥CD′,CD′⊂平面AD′C,A′B⊄平面AD′C,∴A′B∥平面AD′C.5.下列四个正方体中,A,B,C为所在棱的中点,则能得出平面ABC∥平面DEF的是( )【答案解析】答案为:B;解析:在B中,如图,连接MN,PN,∵A,B,C为正方体所在棱的中点,∴AB∥MN,AC∥PN,∵MN∥DE,PN∥EF,∴AB∥DE,AC∥EF,∵AB∩AC=A,DE∩EF=E,AB、AC⊂平面ABC,DE、EF⊂平面DEF,∴平面ABC∥平面DEF,故选B.6.在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,若A1M=AN=,则MN与平面BB1C1C的位置关系是( )A.相交 B.平行 C.垂直 D.不能确定【答案解析】答案为:B解析:连接CD1,在CD1上取点P,使D1P=,∴MP∥BC,PN∥AD1.∴MP∥平面BB1C1C,PN∥平面AA1D1D.∴平面MNP∥平面BB1C1C,∴MN∥平面BB1C1C.故选B.7.已知平面α∥平面β,P是α,β外一点,过点P的直线m与α,β分别交于点A,C,过点P的直线n与α,β分别交于点B,D,且PA=6,AC=9,PD=8,则BD=( )A.16 B.24或4.8 C.14 D.20【答案解析】答案为:B;解析:设BD=x,由α∥β⇒AB∥CD⇒△PAB∽△PCD⇒=.①当点P在两平面之间时,如图(1),则有=,∴x=24;②当点P在两平面外侧时,如图(2),则有=,∴x=,故选B.8.如图所示,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下列五个结论:①PD∥平面AMC;②OM∥平面PCD;③OM∥平面PDA;④OM∥平面PBA;⑤OM∥平面PBC.其中不正确的结论的个数有( )A.1 B.2 C.3 D.4【答案解析】答案为:B解析:矩形ABCD的对角线AC与BD交于点O,所以O为BD的中点.在△PBD中,M是PB的中点,所以OM是△PBD的中位线,OM∥PD,则PD∥平面AMC,OM∥平面PCD,且OM∥平面PDA.因为M∈PB,所以OM与平面PBA、平面PBC相交.9.设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m∥l,且m⊥α,则l⊥α;②若m⊥l,m⊥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=m,β∩γ=l,γ∩α=n,且n∥β,则l∥m.其中正确命题的个数是( )A.1 B.2 C.3 D.4【答案解析】答案为:B解析:对①,两条平行线中有一条与一平面垂直,则另一条也与这个平面垂直,故①正确;对②,直线l可能在平面α内,故②错误;对③,三条交线除了平行,还可能相交于同一点,故③错误;对④,结合线面平行的判定定理和性质定理可判断其正确.综上①④正确.故选B.10.在如图所示的正方体ABCDA1B1C1D1中,E,F分别为棱AB和棱AA1的中点,点M,N分别为线段D1E,C1F上的点,则与平面ABCD平行的直线MN有( )A.无数条 B.2条 C.1条 D.0条【答案解析】答案为:A.解析:法一:取BB1的中点H,连接FH,则FH∥C1D1,连接HE,D1H,在D1E上任取一点M,取D1E的中点O,连接OH,在平面D1HE中,作MG平行于HO,交D1H于G,连接DE,取DE的中点K,连接KB,OK,则易证得OH∥KB.过G作GN∥FH,交C1F于点N,连接MN,由于GM∥HO,HO∥KB,KB平面ABCD,GM平面ABCD,所以GM∥平面ABCD,同理,NG∥平面ABCD,又GM∩NG=G,由面面平行的判定定理得,平面MNG∥平面ABCD,则MN∥平面ABCD.由于M为D1E上任意一点,故与平面ABCD平行的直线MN有无数条.故选A.法二:因为直线D1E,C1F与平面ABCD都相交,所以只需要把平面ABCD向上平移,与线段D1E的交点为M,与线段C1F的交点为N,由面面平行的性质定理知MN∥平面ABCD,故有无数条直线MN∥平面ABCD,故选A.]11.如图所示,侧棱与底面垂直,且底面为正方形的四棱柱ABCDA1B1C1D1中,AA1=2,AB=1,M,N分别在AD1,BC上移动,始终保持MN∥平面DCC1D1,设BN=x,MN=y,则函数y=f(x)的图象大致是( ) 【答案解析】答案为:C.解析:过M作MQ∥DD1,交AD于点Q,连接QN.∵MN∥平面DCC1D1,MQ∥平面DCC1D1,MN∩MQ=M,∴平面MNQ∥平面DCC1D1.又平面ABCD与平面MNQ和DCC1D1分别交于QN和DC,∴NQ∥DC,可得QN=CD=AB=1,AQ=BN=x,∵==2,∴MQ=2x.在Rt△MQN中,MN2=MQ2+QN2,即y2=4x2+1,∴y2-4x2=1(x≥0,y≥1),∴函数y=f(x)的图象为焦点在y轴上的双曲线上支的一部分.故选C.12.如图,ABCDA1B1C1D1是棱长为a的正方体,M,N分别是棱A1B1,B1C1的中点,P是棱AD上一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=( )A.a B.a C.a D.a【答案解析】答案为:A;解析:因为ABCDA1B1C1D1是棱长为a的正方体,所以平面ABCD∥平面A1B1C1D1,又P是棱AD上一点,过P,M,N的平面交上底面于PQ,Q在CD上,所以MN∥PQ,又M,N分别是棱A1B1,B1C1的中点,AP=,所以CQ=,所以DP=DQ=,所以PQ==.二 、填空题13.如图所示,设正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=,过B1,D1,P的平面交平面ABCD于PQ,Q在直线CD上,则PQ= .【答案解析】答案为:a.解析:如图,∵平面A1B1C1D1∥平面ABCD,而平面B1D1P∩平面ABCD=PQ,平面B1D1P∩平面A1B1C1D1=B1D1,∴B1D1∥PQ.又∵B1D1∥BD,∴BD∥PQ,设PQ∩AB=M,∵AB∥CD,∴△APM∽△DPQ.∴==2,即PQ=2PM.又知△APM∽△ADB,∴==,∴PM=BD,又BD=a,∴PQ=a.14.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为________.【答案解析】答案为:平行四边形解析:∵平面ABFE∥平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,∴EF∥HG.同理EH∥FG,∴四边形EFGH的形状是平行四边形.15.在三棱锥PABC中,PB=6,AC=3,G为△PAC的重心,过点G作三棱锥的一个截面,使截面平行于PB和AC,则截面的周长为 .【答案解析】答案为:8.解析:过点G作EF∥AC,分别交PA,PC于点E,F,过点E作EN∥PB交AB于点N,过点F作FM∥PB交BC于点M,连接MN,则四边形EFMN是平行四边形(平面EFMN为所求截面),且EF=MN=AC=2,FM=EN=PB=2,所以截面的周长为2×4=8.16.如图是一张矩形白纸ABCD,AB=10,AD=10,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,且A、C在平面BFDE同侧,下列命题正确的是 .(写出所有正确命题的序号)①当平面ABE∥平面CDF时,AC∥平面BFDE;②当平面ABE∥平面CDF时,AE∥CD;③当A、C重合于点P时,PG⊥PD;④当A、C重合于点P时,三棱锥P-DEF的外接球的表面积为150π.【答案解析】答案为:①④;解析:在△ABE中,tan∠ABE=,在△ACD中,tan∠CAD=,所以∠ABE=∠DAC,由题意,将△ABE,△DCF沿BE,DF折起,且A,C在平面BEDF同侧,此时A、C、G、H四点在同一平面内,平面ABE∩平面AGHC=AG,平面CDF∩平面AGHC=CH,当平面ABE∥平面CDF时,得到AG∥CH,显然AG=CH,所以四边形AGHC为平行四边形,所以AC∥GH,进而可得AC∥平面BFDE,故①正确;由于折叠后,直线AE与直线CD为异面直线,所以AE与CD不平行,故②不正确;当A、C重合于点P时,可得PG=,PD=10,又GD=10,∴PG2+PD2≠GD2,所以PG与PD不垂直,故③不正确;当A,C重合于点P时,在三棱锥P-DEF中,△EFD与△FCD均为直角三角形,所以DF为外接球的直径,即R==,所以外接球的表面积为S=4πR2=4π×2=150π,故④正确.综上,正确命题的序号为①④.
相关试卷
这是一份2023年高考数学(理数)一轮复习课时40《空间向量》达标练习(含详解),文件包含2023年高考数学理数一轮复习课时40《空间向量》达标练习教师版doc、2023年高考数学理数一轮复习课时40《空间向量》达标练习含详解doc等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。
这是一份2023年高考数学(理数)一轮复习课时39《空间线、面的垂直关系》达标练习(含详解),文件包含2023年高考数学理数一轮复习课时39《空间线面的垂直关系》达标练习含详解doc、2023年高考数学理数一轮复习课时39《空间线面的垂直关系》达标练习教师版doc等2份试卷配套教学资源,其中试卷共12页, 欢迎下载使用。
这是一份2023年高考数学(理数)一轮复习课时37《空间点、线、面的位置关系》达标练习(含详解),文件包含2023年高考数学理数一轮复习课时37《空间点线面的位置关系》达标练习含详解doc、2023年高考数学理数一轮复习课时37《空间点线面的位置关系》达标练习教师版doc等2份试卷配套教学资源,其中试卷共11页, 欢迎下载使用。








