

广西专用高考数学一轮复习考点规范练10幂函数与二次函数含解析新人教A版文
展开考点规范练10 幂函数与二次函数
基础巩固
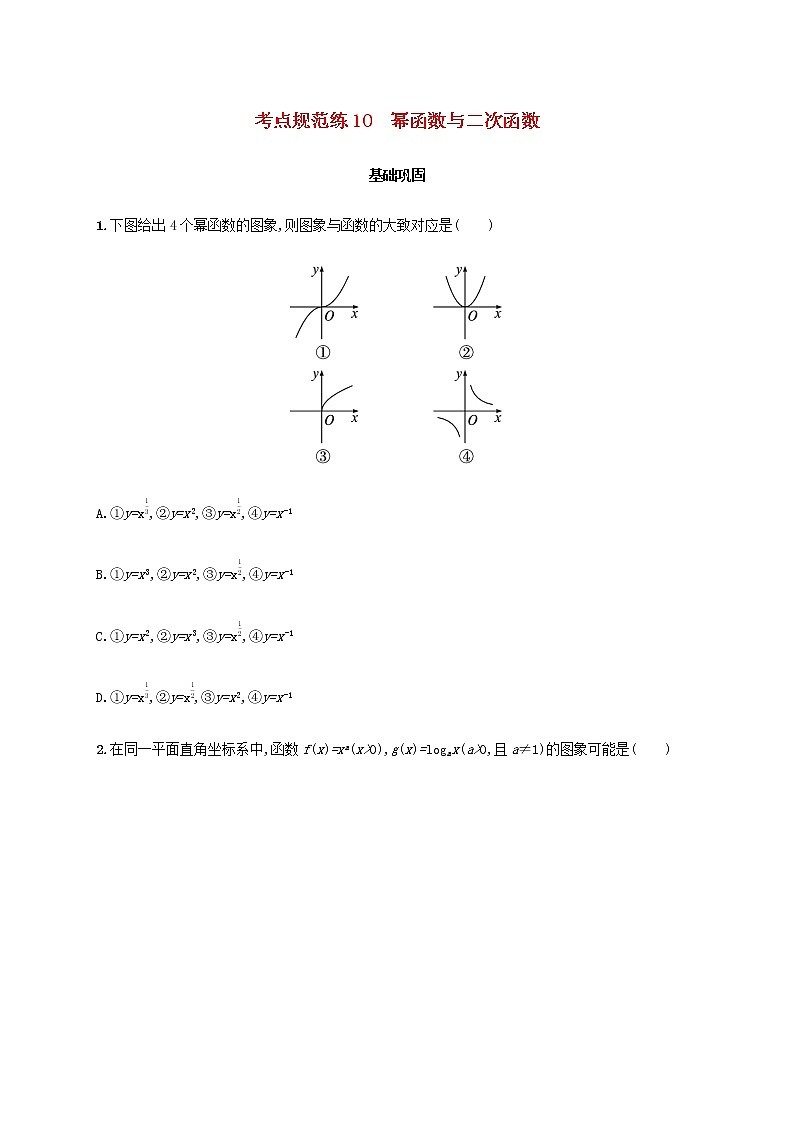
1.下图给出4个幂函数的图象,则图象与函数的大致对应是( )
A.①y=,②y=x2,③y=,④y=x-1
B.①y=x3,②y=x2,③y=,④y=x-1
C.①y=x2,②y=x3,③y=,④y=x-1
D.①y=,②y=,③y=x2,④y=x-1
2.在同一平面直角坐标系中,函数f(x)=xa(x>0),g(x)=logax(a>0,且a≠1)的图象可能是( )
3.若函数y=x2-3x-4的定义域为[0,m],值域为,则m的取值范围是( )
A.[0,4] B.
C. D.
4.若函数f(x)=x2-|x|-6,则f(x)的零点个数为( )
A.1 B.2
C.3 D.4
5.对于幂函数f(x)=,若0<x1<x2,则f的大小关系是( )
A.f
B.f
C.f
D.无法确定
6.已知函数f(x)=x2-bx+c满足f(x+1)=f(1-x),且f(0)=3,则f(bx)与f(cx)的大小关系是( )
A.与x有关,不确定
B.f(bx)≥f(cx)
C.f(bx)>f(cx)
D.f(bx)≤f(cx)
7.若关于x的不等式x2+ax+1≥0对于一切x∈恒成立,则a的最小值是( )
A.0
B.2
C.-
D.-3
8.已知二次函数f(x)的图象过点(0,1),对称轴为x=2,最小值为-1,则它的解析式为 .
9.若幂函数f(x)=(m2-5m+7)xm在R上为增函数,则logm+2lg 5+lg 4+= .
10.(2021广西崇左模拟)若函数f(x)=-x2+4ax在区间[1,3]上不单调,则实数a的取值范围是 .
11.(2021四川内江诊断测试)若函数f(x)=x2+ax在区间[1,2]上的最大值为a+1,则a的取值范围为 .
12.已知幂函数f(x)=,若f(a+1)<f(10-2a),则a的取值范围是 .
能力提升
13.已知幂函数f(x)=(m-1)2·在区间(0,+∞)内单调递增,函数g(x)=2x-t,若对于任意的x1∈[1,5),总存在x2∈[1,5)使得f(x1)=g(x2),则t的取值范围是( )
A.⌀
B.t≥7或t≤1
C.t>7或t<1
D.1≤t≤7
14.(2021广东普宁模拟)如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点的纵坐标在区间[2,3]上,有以下结论:
①当x>3时,y<0;
②4a+2b+c=0;
③-1≤a≤-;
④3a+b>0.
其中正确的有 .(填序号)
15.(2021江苏南通高三检测)已知f(x)=x2+x+11,g(x)=[f(x)-x2-13]·|x|,则函数g(x)在区间[t,2]上的最大值是 ,最小值是 .
高考预测
16.(2021陕西安康高三质检)已知函数f(x)=2x2-mx-3m,则“m>2”是“f(x)<0对x∈[1,3]恒成立”的( )
A.充分不必要条件
B.充要条件
C.必要不充分条件
D.既不充分也不必要条件
答案:
1.B 解析②的图象关于y轴对称,②应为偶函数,故排除选项C,D,
由①的图象知,在第一象限内,图象下凸,递增的较快,所以幂函数的指数大于1,故排除选项A.
2.D 解析由于本题中函数为y=xa(x>0)与y=logax,对于选项A,没有幂函数图象,故错误;
对于选项B,由y=xa(x>0)的图象知a>1,而由y=logax的图象知0<a<1,故B错误;
对于选项C,由y=xa(x>0)的图象知0<a<1,而由y=logax的图象知a>1,故C错误;
对于选项D,由y=xa(x>0)的图象知0<a<1,而由y=logax的图象知0<a<1,故选D.
3.D 解析二次函数图象的对称轴的方程为x=,且f=-,f(3)=f(0)=-4,结合图象可得m∈.
4.B 解析当x>0时,由x2-x-6=0,解得x=-2或x=3,可知x=3;
当x<0时,由x2+x-6=0,解得x=2或x=-3,可知x=-3;
故f(x)的零点个数为2.故选B.
5.A 解析∵幂函数f(x)=在区间(0,+∞)内单调递增,图象是上凸的,
∴当0<x1<x2时,应有f.
6.D 解析因为f(x+1)=f(1-x),所以=1,即b=2,
因为f(0)=3,所以c=3,所以bx=2x,cx=3x,
若x<0,则有0<cx<bx<1,而f(x)在区间(-∞,1)内单调递减,所以f(bx)<f(cx);
若x=0,则有cx=bx=1,此时有f(bx)=f(cx);
若x>0,则有1<bx<cx,而f(x)在区间(1,+∞)内单调递增,所以f(bx)<f(cx).
综合可得f(bx)≤f(cx).
7.C 解析由x2+ax+1≥0得a≥-在x∈上恒成立.
令g(x)=-,则g(x)在区间上为增函数,
所以g(x)max=g=-,所以a≥-.
8.f(x)=(x-2)2-1 解析依题意可设f(x)=a(x-2)2-1.
∵函数图象过点(0,1),∴4a-1=1.
∴a=.∴f(x)=(x-2)2-1.
9.4 解析由题意得m2-5m+7=1,解得m=2或m=3.
因为f(x)在R上为增函数,所以m=3,所以f(x)=x3,
故logm+2lg5+lg4+
=log3+2lg10+
=+2+=4.
10. 解析由题意得f(x)=-x2+4ax图象的对称轴为直线x=2a,
因为函数f(x)在区间[1,3]上不单调,所以1<2a<3,得<a<.
11.(-∞,-3] 解析∵f(x)=x2+ax图象的对称轴为直线x=-,
当a>-3,即-时,f(x)max=f(2)=4+2a=a+1,解得a=-3,不符合题意,舍去;
当a≤-3,即-时,f(x)max=f(1)=1+a,符合题意,故a≤-3.
综上可知,a的取值范围为(-∞,-3].
12.(3,5) 解析∵f(x)=(x>0),
∴f(x)是定义在区间(0,+∞)内的减函数.
又f(a+1)<f(10-2a),
∴解得∴3<a<5.
13.D 解析∵幂函数f(x)=(m-1)2在区间(0,+∞)内单调递增,∴解得m=0,∴f(x)=x2.
当x1∈[1,5)时,f(x1)∈[1,25),设集合A=[1,25),
又当x2∈[1,5)时,g(x2)∈[2-t,32-t),设集合B=[2-t,32-t),
由题意得A⊆B,∴解得1≤t≤7.
14.①③ 解析依题意抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),顶点坐标为(1,n),
所以抛物线与x轴的另一交点为(3,0),所以当x>3时,y<0,故①正确;
当x=2时,y=4a+2b+c>0,故②错误;
∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),且a<0,
∴a-b+c=0,又-=1,即b=-2a,∴a+2a+c=0,2a+b=0,
∴3a+b<0,c=-3a,∵2≤c≤3,∴2≤-3a≤3,
∴-1≤a≤-,∴③正确,④错误.
15.0 解析g(x)=(x2+x+11-x2-13)·|x|=(x-2)·|x|=
因为g(1)=-1,当x<0时,由-x2+2x=-1解得x=1-.
因为x∈[t,2],所以当1≤t<2时,g(x)=x2-2x在区间[t,2]上单调递增,
所以g(x)max=g(2)=0,g(x)min=g(t)=t2-2t;
当0≤t<1时,g(x)=x2-2x在区间(t,1)上单调递减,在区间(1,2)上单调递增,
所以g(x)max=g(2)=0,g(x)min=g(1)=-1;
当1-≤t<0时,因为x∈[t,0)时,g(x)=-x2+2x在区间[t,0)上单调递增,
则-1=g(1-)≤g(t)≤g(x)<g(0)=0;x∈[0,2]时,g(x)=x2-2x在区间(0,1)上单调递减,在区间(1,2)上单调递增,所以g(x)∈[g(1),g(2)],即g(x)∈[-1,0],
所以g(x)max=g(2)=0,g(x)min=g(1)=-1;
当t<1-时,因为x∈[t,0)时,g(x)=-x2+2x在区间[t,0)上单调递增,所以g(t)≤g(x)<g(0)=0,g(t)<g(1-)=-1;x∈[0,2]时,g(x)=x2-2x∈[-1,0],
所以g(x)max=g(2)=0,g(x)min=g(t)=-t2+2t.
综上,函数g(x)在区间[t,2]上的最大值g(x)max=g(2)=0,
最小值g(x)min=
16.C 解析若f(x)<0对x∈[1,3]恒成立,则解得m>3,{m|m>3}是{m|m>2}的真子集,所以“m>2”是“f(x)<0对x∈[1,3]恒成立”的必要不充分条件.
广西专用2022年高考数学一轮复习考点规范练10幂函数与二次函数含解析新人教A版文: 这是一份广西专用2022年高考数学一轮复习考点规范练10幂函数与二次函数含解析新人教A版文,共7页。
高考数学一轮复习考点规范练10幂函数与二次函数含解析新人教A版文: 这是一份高考数学一轮复习考点规范练10幂函数与二次函数含解析新人教A版文,共8页。试卷主要包含了若a<0,则0,5aB等内容,欢迎下载使用。
高考数学一轮复习考点规范练10幂函数与二次函数含解析新人教A版理: 这是一份高考数学一轮复习考点规范练10幂函数与二次函数含解析新人教A版理,共8页。试卷主要包含了若a<0,则0,5aB等内容,欢迎下载使用。












