广西专用高考数学一轮复习考点规范练11函数的图象含解析新人教A版文

考点规范练11　函数的图象

基础巩固

1.(2021云南昭通高三期末)函数f(x)=的大致图象为(　　)

2.(2021浙江高考)已知函数f(x)=x2+,g(x)=sin x,则图中曲线对应的函数可能是(　　)

A.y=f(x)+g(x)-

B.y=f(x)-g(x)-

C.y=f(x)g(x)

D.y=

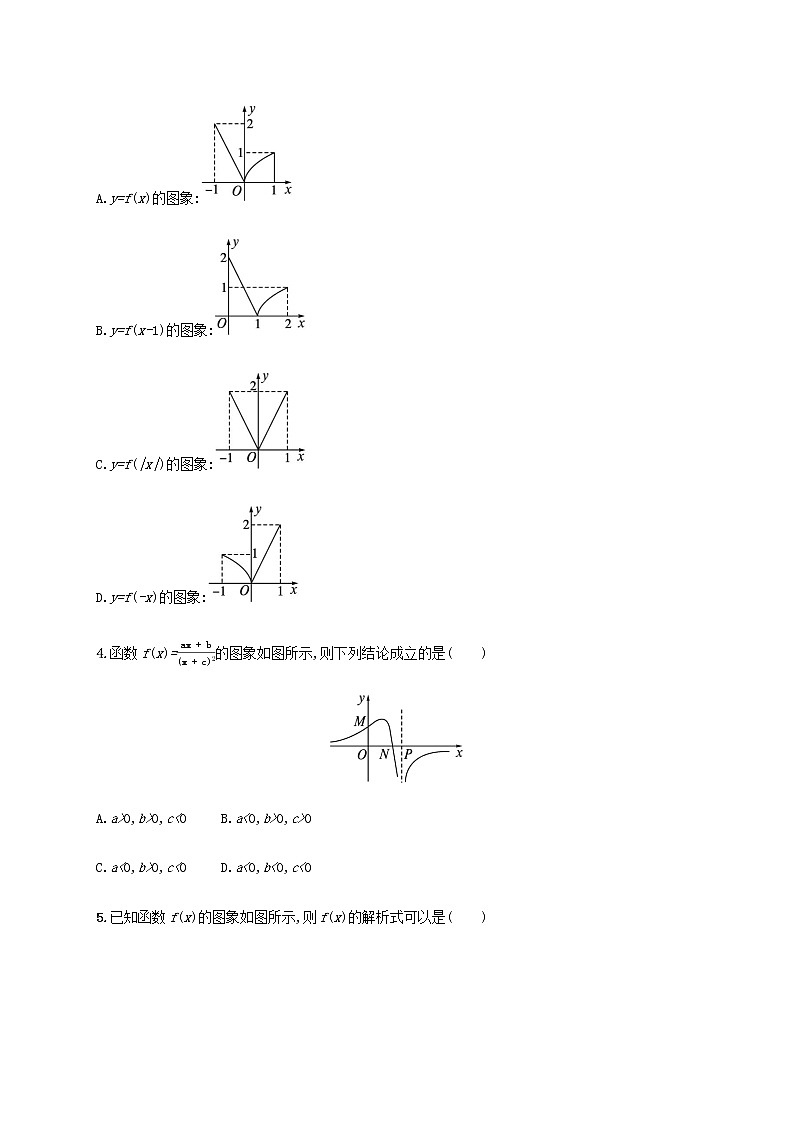
3.(2021广东中山纪念中学高三月考)已知函数f(x)=则下列图象错误的是(　　)

A.y=f(x)的图象:

B.y=f(x-1)的图象:

C.y=f(|x|)的图象:

D.y=f(-x)的图象:

4.函数f(x)=的图象如图所示,则下列结论成立的是(　　)

A.a>0,b>0,c<0 B.a<0,b>0,c>0

C.a<0,b>0,c<0 D.a<0,b<0,c<0

5.已知函数f(x)的图象如图所示,则f(x)的解析式可以是(　　)

A.f(x)=

B.f(x)=

C.f(x)=-1

D.f(x)=x-

6.已知函数f(x)=x2+ex-(x<0)与g(x)=x2+ln(x+a)的图象上存在关于y轴对称的点,则a的取值范围是(　　)

A.-∞, B.(-∞,)

C.- D.-

7.定义在R上的函数f(x)=若关于x的方程f(x)=c(c为常数)恰有3个不同的实数根x1,x2,x3,则x1+x2+x3=　　　　　. 

8.若函数y=f(x)的图象过点(1,1),则函数f(4-x)的图象一定经过点　　　　　. 

9.不等式3sinx-lox<0的整数解的个数为　　　　. 

能力提升

10.已知函数f(x)=x-4+,x∈(0,4),当x=a时,f(x)取得最小值b,则函数g(x)=a|x+b|的大致图象为(　　)

11.对于函数f(x)=lg(|x-2|+1),给出如下三个命题:①f(x+2)是偶函数;②f(x)在区间(-∞,2)内是减函数,在区间(2,+∞)内是增函数;③f(x)没有最小值.其中正确的个数为(　　)

A.1 B.2 C.3 D.0

12.已知函数f(x)=函数g(x)=b-f(2-x),其中b∈R,若函数y=f(x)-g(x)恰有4个零点,则b的取值范围是(　　)

A. B.

C. D.

13.已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=x,且在区间[-1,3]上,关于x的方程f(x)=kx+k+1(k∈R,k≠-1)有四个根,则k的取值范围是　　　　　　　. 

高考预测

14.(2021北京石景山一模)已知f(x)=若|f(x)|≥ax对x∈[-1,1]恒成立,则实数a的取值范围是(　　)

A.(-∞,-1]∪[0,+∞)

B.[0,1]

C.[-1,0]

D.(-1,0)

答案：

1.A　解析函数f(x)=的定义域为(-∞,0)∪(0,+∞),

且f(x)=,f(-x)==f(x),所以函数f(x)为偶函数,

排除B,C选项;

当0<x<1时,lnx<0,则f(x)=<0,排除D选项.

2.D　解析对于A,y=f(x)+g(x)-=x2+sinx,该函数为非奇非偶函数,与题中图象不符,排除A;

对于B,y=f(x)-g(x)-=x2-sinx,该函数为非奇非偶函数,与题中图象不符,排除B;

对于C,y=f(x)g(x)=sinx,则y'=2xsinx+cosx,

当x=时,y'=>0,与题中图象不符,排除C.

故选D.

3.C　解析先作出f(x)=的图象,如图所示,所以A正确;

对于B,y=f(x-1)的图象是由f(x)的图象向右平移1个单位长度得到的,故B正确;

对于C,当x>0时,y=f(|x|)的图象与f(x)的图象相同,且函数y=f(|x|)的图象关于y轴对称,故C错误;

对于D,y=f(-x)的图象与f(x)的图象关于y轴对称,故D正确.

4.C　解析由题中图象知f(0)=>0,因此b>0.

函数f(x)的定义域为(-∞,-c)∪(-c,+∞),

因此-c>0,c<0.而当x→+∞时,f(x)<0,

可得a<0,故选C.

5.A　解析由题中函数图象可知,函数f(x)为奇函数,故排除B,C.

若函数为f(x)=x-,

则当x→+∞时,f(x)→+∞,与图象不符,故排除D.

故选A.

6.B　解析由已知得与函数f(x)的图象关于y轴对称的图象对应的函数解析式为h(x)=x2+e-x-(x>0).

令h(x)=g(x),得ln(x+a)=e-x-(x>0),作函数M(x)=e-x-(x>0)的图象,显然当a≤0时,函数y=ln(x+a)的图象与M(x)的图象一定有交点.

当a>0时,若函数y=ln(x+a)的图象与M(x)的图象有交点,则lna<,则0<a<.

综上,a<.故选B.

7.0　解析函数f(x)的图象如图,方程f(x)=c有3个不同的实数根,

即y=f(x)与y=c的图象有3个交点,易知c=1,且一根为0.

由lg|x|=1知另两根为-10和10,故x1+x2+x3=0.

8.(3,1)　解析由于函数y=f(4-x)的图象可以看作y=f(x)的图象先关于y轴对称,再向右平移4个单位得到.点(1,1)关于y轴对称的点为(-1,1),再将此点向右平移4个单位可推出函数y=f(4-x)的图象过点(3,1).

9.2　解析不等式3sin-lox<0,即3sin<lox.设f(x)=3sin,g(x)=lox,在同一平面直角坐标系中分别作出函数f(x)与g(x)的图象,由图象可知,当f(x)<g(x)时,x可取的整数有3,7,所以不等式3sin-lox<0的整数解的个数为2.

10.A　解析∵x∈(0,4),∴x+1>1,

∴f(x)=x-4+=x+1+-5≥2-5=1,

当且仅当x=2时取等号,此时函数f(x)有最小值1,

∴a=2,b=1,此时g(x)=2|x+1|=

此函数可以看成将函数y=的图象向左平移1个单位长度得到,结合指数函数的图象及选项可知A正确.

11.B　解析因为函数f(x)=lg(|x-2|+1),

所以函数f(x+2)=lg(|x|+1)是偶函数.

由y=lgx

y=lg(x+1)

y=lg(|x|+1)y=lg(|x-2|+1),如图,可知f(x)在区间(-∞,2)内是减函数,在区间(2,+∞)内是增函数.

由图象可知函数存在最小值为0.所以①②正确.

12.D　解析由f(x)=

得f(x)=

故f(2-x)=

所以f(x)+f(2-x)=

因为函数y=f(x)-g(x)=f(x)+f(2-x)-b恰有4个零点,

所以直线y=b与函数y=f(x)+f(2-x)的图象有4个不同的交点.

画出函数y=f(x)+f(2-x)的大致图象,如图.

由图可知,当b∈时,直线y=b与函数y=f(x)+f(2-x)的图象有4个不同的交点.故选D.

13.　解析由题意作出f(x)在区间[-1,3]上的图象,如图所示.

记y=k(x+1)+1,则函数y=k(x+1)+1的图象过定点A(-1,1).

记B(2,0),由图象知,方程f(x)=kx+k+1有四个根,

即函数f(x)的图象与直线y=kx+k+1有四个交点,

故kAB<k<0.

又kAB==-,故-<k<0.

14.C　解析作出y=|f(x)|,y=ax在区间[-1,1]上的图象如图所示.

因为|f(x)|≥ax对x∈[-1,1]恒成立,所以y=|f(x)|的图象在直线y=ax的上方(可以部分点重合).又|f(-1)|=|1-2|=1,令3x-2=0,得x=,所以A(-1,1),B.

根据图象可知,当直线y=ax经过点A(-1,1)时,a有最小值,且amin=-1,

当直线y=ax经过点B时,a有最大值,且amax=0.

综上可知,a的取值范围是[-1,0].