广西专用高考数学一轮复习考点规范练33二元一次不等式组与简单的线性规划问题含解析新人教A版文

考点规范练33　二元一次不等式(组)与简单的线性规划问题

基础巩固

1.(2021山东春季高考)不等式组表示的区域(阴影部分)是(　　)

2.(2021全国Ⅰ)若x,y满足约束条件则z=3x+y的最小值为(　　)

A.18 B.10 C.6 D.4

3.已知点A(2,1),O是坐标原点,点P(x,y)的坐标满足设z=,则z的最大值是(　　)

A.-6 B.1 C.2 D.4

4.如图,其中A(5,3),B(1,1),C(1,5),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值是(　　)

A.　　　　　　　　　B.

C.2　　　　　　　　　　D.

5.已知实数x,y满足则z=ax+y(a>0)的最小值为(　　)

A.0 B.a C.2a+1 D.-1

6.已知点(m+n,m-n)在表示的平面区域内,则m2+n2的最小值为(　　)

A. B. C. D.

7.(2021广西桂林质量检测)已知x,y满足若使得z=ax+y取得最大值的点(x,y)有无数个,则a的值等于　　　　. 

8.某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨、B原料2吨;生产每吨乙产品要用A原料1吨、B原料3吨.销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨、B原料不超过18吨,则该企业可获得的最大利润是　　　　　万元. 

9.已知实数x,y满足则x2+y2的取值范围是　　　　　. 

能力提升

10.若实数x,y满足约束条件则z=2|x|-y的最小值是(　　)

A.- B.5 C.-1 D.-2

11.若实数x,y满足且2x+y-3≥k(x-2)恒成立,则k的取值范围是(　　)

A.(-∞,-1] B.(-∞,1]

C.[-1,+∞) D.[1,+∞)

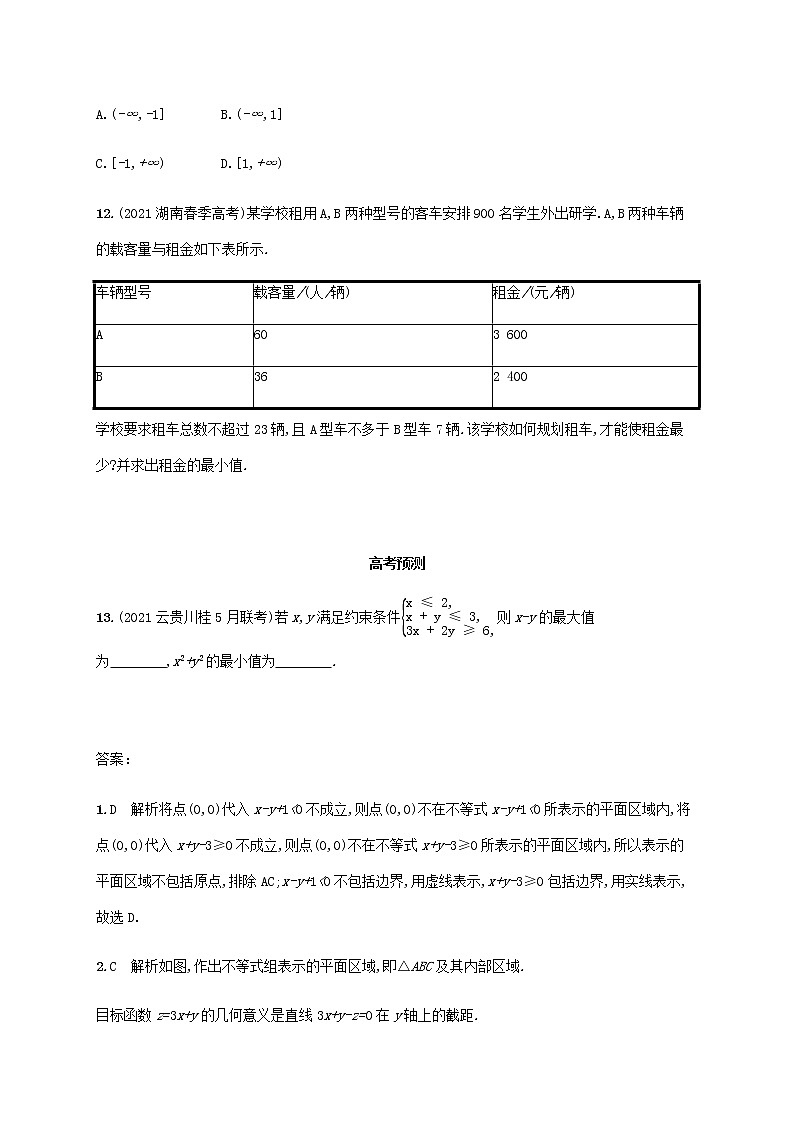
12.(2021湖南春季高考)某学校租用A,B两种型号的客车安排900名学生外出研学.A,B两种车辆的载客量与租金如下表所示.

学校要求租车总数不超过23辆,且A型车不多于B型车7辆.该学校如何规划租车,才能使租金最少?并求出租金的最小值.

高考预测

13.(2021云贵川桂5月联考)若x,y满足约束条件则x-y的最大值为　　　　,x2+y2的最小值为　　　　. 

答案：

1.D　解析将点(0,0)代入x-y+1<0不成立,则点(0,0)不在不等式x-y+1<0所表示的平面区域内,将点(0,0)代入x+y-3≥0不成立,则点(0,0)不在不等式x+y-3≥0所表示的平面区域内,所以表示的平面区域不包括原点,排除AC;x-y+1<0不包括边界,用虚线表示,x+y-3≥0包括边界,用实线表示,故选D.

2.C　解析如图,作出不等式组表示的平面区域,即△ABC及其内部区域.

目标函数z=3x+y的几何意义是直线3x+y-z=0在y轴上的截距.

作出直线l:3x+y-z=0.

由图可知,当直线l过点C时,直线l在y轴上的截距最小,即z取得最小值.

由解得即C(1,3).

故z的最小值为3×1+3=6.

3.D　解析由题意,作出可行域如图中阴影部分所示.z==2x+y,作出直线2x+y=0并平移,可知当直线过点C时,z取得最大值.

由

即C(1,2),则z的最大值是4,故选D.

4.B　解析直线y=-ax+z(a>0)的斜率为-a<0,当直线y=-ax平移到直线AC位置时取得最大值的最优解有无穷多个.

∵kAC=-,∴-a=-,即a=.

5.D　解析由约束条件作出可行域(阴影部分),如图.

化目标函数z=ax+y(a>0)为y=-ax+z,

由图可知,当直线y=-ax+z过点A(0,-1)时,直线在y轴上的截距最小,z有最小值为-1.

6.D　解析作出不等式组所表示的平面区域,即可行域,如图所示.

已知点(m+n,m-n)在可行域内,则所以m=,n=,

所以m2+n2=(x2+y2).

所以m2+n2的最小值即为可行域内的点与原点的距离的最小值平方的一半.

由图可知,可行域内的点与坐标原点的距离的最小值即为原点到直线2x-y-2=0的距离,所以距离的最小值为.

所以m2+n2的最小值为.

7.-1　解析先根据约束条件画出可行域,如图所示.

当直线z=ax+y和直线AB重合时,z取得最大值的点(x,y)有无数个,

∴-a=kAB=1(kAB为直线AB的斜率),所以a=-1.

8.27　解析设生产甲产品x吨、乙产品y吨,

则获得的利润为z=5x+3y.

由题意得此不等式组表示的平面区域(阴影部分),如图所示.

由图可知当y=-x+经过点A时,z取得最大值,此时x=3,y=4,zmax=5×3+3×4=27(万元).

9.　解析画出约束条件对应的可行域(如图中阴影部分所示),x2+y2表示原点到可行域中的点的距离的平方,由图知原点到直线2x+y-2=0的距离的平方为x2+y2的最小值,为,原点到点(2,3)的距离的平方为x2+y2的最大值,为22+32=13.

因此x2+y2的取值范围是.

10.C　解析作出实数x,y满足约束条件所表示的平面区域,即可行域,如图所示.

由已知可得点A,B,C,D的坐标分别为A,B,C(-2,-1),D(0,1).

若x≥0,则z=2|x|-y可化为y=2x-z,由图可知,当直线y=2x-z过点D时,直线在y轴上的截距最大,此时z取得最小值-1.

若x<0,则z=2|x|-y可化为y=-2x-z,由图可知,当直线y=-2x-z过点D时,直线在y轴上的截距最大,此时z取得最小值-1.故选C.

11.D　解析作出不等式组所表示的平面区域,即可行域,它为△ABC,其中A(1,2),B(0,3),C(0,1),如图所示.

∵对于可行域内任一点P(x,y),都有0≤x≤1,

∴x-2<0.∴2x+y-3≥k(x-2),

即为k≥=2+恒成立,

转化为求z=2+的最大值,

又的几何意义为点P(x,y)和点M(2,-1)连线的斜率,

由图可知,kMA≤≤kMC,即-3≤≤-1.

∴z∈[-1,1],即zmax=1.∴k≥1.故选D.

12.解设A型车和B型车分别为x,y辆,则租金为z=3600x+2400y,

依题意,x,y需满足

如图,作出可行域.

令z=0,目标函数变形为3x+2y=0,即y=-x,当直线平移至点B时,目标函数取得最小值,

由解得此时zmin=3600×12+2400×5=55200(元).

所以A型车和B型车分别为12辆和5辆时,租金最少,租金的最小值是55200元.

13.2　　解析作出可行域,如图.由图可知,当直线z=x-y过B(2,0)时,z取得最大值2.

x2+y2表示可行域内点(x,y)到原点距离的平方,

原点到直线3x+2y=6的距离为d=,

所以x2+y2的最小值是.