

所属成套资源:全套广西专用高考数学一轮复习大题专项练含解析新人教A版理
广西专用高考数学一轮复习大题专项练4高考中的立体几何含解析新人教A版理
展开
这是一份广西专用高考数学一轮复习大题专项练4高考中的立体几何含解析新人教A版理,共15页。
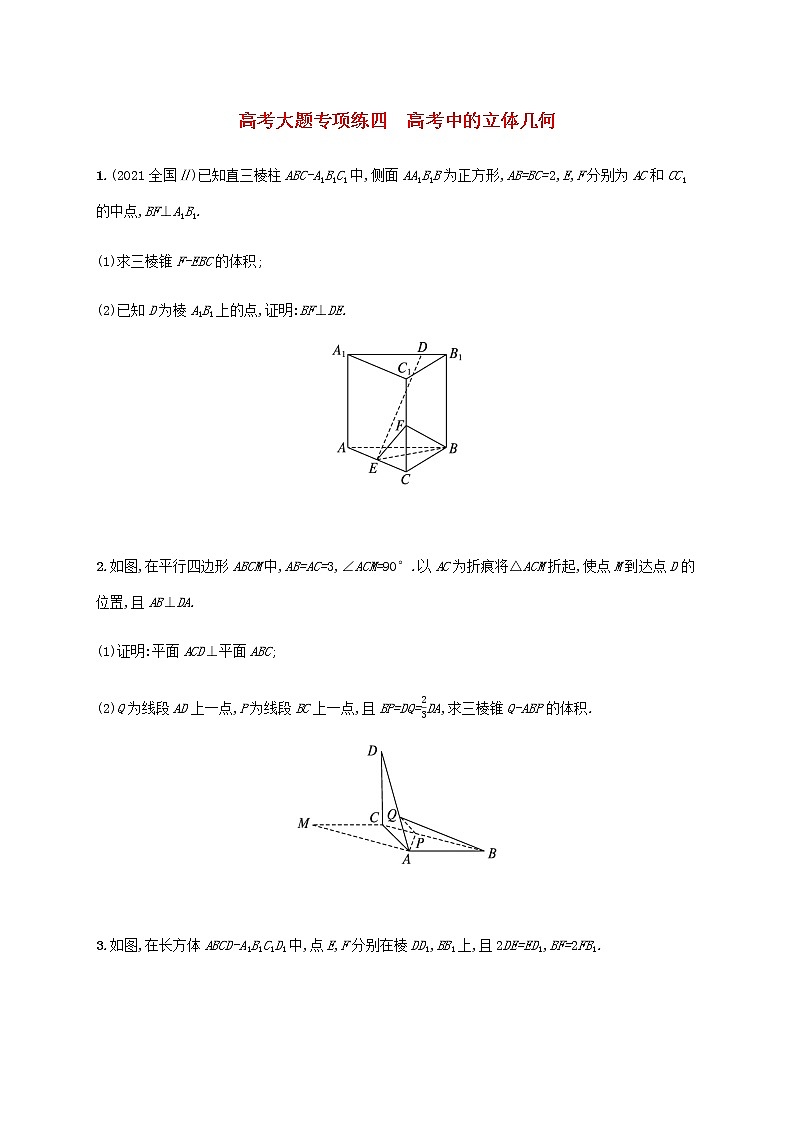
高考大题专项练四 高考中的立体几何1.(2021全国Ⅱ)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,BF⊥A1B1.(1)求三棱锥F-EBC的体积;(2)已知D为棱A1B1上的点,证明:BF⊥DE. 2.如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°.以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=DA,求三棱锥Q-ABP的体积. 3.如图,在长方体ABCD-A1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE=ED1,BF=2FB1.(1)证明:点C1在平面AEF内;(2)若AB=2,AD=1,AA1=3,求二面角A-EF-A1的正弦值. 4.(2021全国Ⅰ)如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM.(1)求BC;(2)求二面角A-PM-B的正弦值. 5.如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且.(1)求证:CD⊥平面PAD;(2)求二面角F-AE-P的余弦值;(3)设点G在PB上,且,判断直线AG是否在平面AEF内,说明理由. 6.如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F;(2)设O为△A1B1C1的中心,若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN所成角的正弦值. 7.(2021天津高考)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱BC的中点,F为棱CD的中点.(1)求证:D1F∥平面A1EC1;(2)求直线AC1与平面A1EC1所成角的正弦值;(3)求二面角A-A1C1-E的正弦值. 8.如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=,且点M和N分别为B1C和D1D的中点.(1)求证:MN∥平面ABCD;(2)求二面角D1-AC-B1的正弦值;(3)设E为棱A1B1上的点,若直线NE和平面ABCD所成角的正弦值为,求线段A1E的长. 答案:1.(1)解在直三棱柱ABC-A1B1C1中,BB1⊥A1B1,∵BF⊥A1B1,BB1∩BF=B,BB1,BF⊂平面BCC1B1,∴A1B1⊥平面BCC1B1.∵AB∥A1B1,∴AB⊥平面BCC1B1,∴AB⊥BC.∵AB=BC=2,∴AC==2,∴CE=BE=.∴CF=CC1=AB=1,∴V三棱锥F-EBC=S△EBC×CF=×1=.(2)证明如图,连接A1E,取BC中点M,连接B1M,EM.∵E,M分别为AC,BC中点,∴EM∥AB.又AB∥A1B1,∴A1B1∥EM,则点A1,B1,M,E四点共面,故DE⊂平面A1B1ME.又在侧面BCC1B1中,△FCB≌△MBB1,∴∠FBM=∠MB1B.又∠MB1B+∠B1MB=90°,∴∠FBM+∠B1MB=90°,∴BF⊥MB1.又BF⊥A1B1,MB1∩A1B1=B1,MB1,A1B1⊂平面A1B1ME,∴BF⊥平面A1B1ME,∴BF⊥DE.2.(1)证明由已知可得,∠BAC=90°,BA⊥AC.又BA⊥AD,AC∩AD=A,所以AB⊥平面ACD.又AB⊂平面ABC,所以平面ACD⊥平面ABC.(2)解由已知可得,DC=CM=AB=3,DA=3.又BP=DQ=DA,所以BP=2.作QE⊥AC,垂足为E,则QEDC.由已知及(1)可得DC⊥平面ABC,所以QE⊥平面ABC,QE=1.由AB=AC,∠BAC=90°,得∠ABC=45°.因此,三棱锥Q-APB的体积为VQ-ABP=QE·S△ABP=×1××3×2×sin45°=1.3.解设AB=a,AD=b,AA1=c,如图,以C1为坐标原点,的方向为x轴正方向,建立空间直角坐标系C1xyz.(1)证明:连接C1F,则C1(0,0,0),A(a,b,c),E,F0,b,c,=0,b,c,=0,b,c,得,因此EA∥C1F,即A,E,F,C1四点共面,所以点C1在平面AEF内.(2)由已知得A(2,1,3),E(2,0,2),F(0,1,1),A1(2,1,0),=(0,-1,-1),=(-2,0,-2),=(0,-1,2),=(-2,0,1).设n1=(x,y,z)为平面AEF的法向量,则即可取n1=(-1,-1,1).设n2为平面A1EF的法向量,则同理可取n2=,2,1.因为cos<n1,n2>==-,所以二面角A-EF-A1的正弦值为.4.解(1)连接BD.∵PD⊥底面ABCD,AM⊂底面ABCD,∴PD⊥AM.∵PB⊥AM,PB∩PD=P,∴AM⊥平面PBD,∴AM⊥BD,∴∠ADB+∠DAM=90°.又∠DAM+∠MAB=90°,∴∠ADB=∠MAB,∴Rt△DAB∽Rt△ABM,∴,∴BC2=1,∴BC=.(2)如图,以D为原点,的方向分别为x,y,z轴的正方向建立空间直角坐标系.可得A(,0,0),B(,1,0),M,1,0,P(0,0,1),=(-,0,1),=(-,-1,1).设平面AMP的法向量为m=(x1,y1,z1),则即令x1=,则y1=1,z1=2,可得m=(,1,2).设平面BMP的法向量为n=(x2,y2,z2),同理可得n=(0,1,1).则cos<m,n>=.设二面角A-PM-B的平面角为θ,则sinθ=.5.(1)证明因为PA⊥平面ABCD,所以PA⊥CD.又因为AD⊥CD,所以CD⊥平面PAD.(2)解过A作AD的垂线交BC于点M.因为PA⊥平面ABCD,所以PA⊥AM,PA⊥AD.如图,建立空间直角坐标系Axyz,则A(0,0,0),B(2,-1,0),C(2,2,0),D(0,2,0),P(0,0,2).因为E为PD的中点,所以E(0,1,1).所以=(0,1,1),=(2,2,-2),=(0,0,2).所以=,-,=.设平面AEF的法向量为n=(x,y,z),则即令z=1,则y=-1,x=-1.于是n=(-1,-1,1).又因为平面PAD的法向量为p=(1,0,0),所以cos<n,p>==-.由题知,二面角F-AE-P为锐角,所以其余弦值为.(3)解直线AG在平面AEF内.因为点G在PB上,且=(2,-1,-2),所以=,-,-,=,-.由(2)知,平面AEF的法向量n=(-1,-1,1).所以·n=-=0.所以直线AG在平面AEF内.6.(1)证明因为M,N分别为BC,B1C1的中点,所以MN∥CC1.又由已知得AA1∥CC1,故AA1∥MN.因为△A1B1C1是正三角形,所以B1C1⊥A1N.又B1C1⊥MN,且MN∩A1N=N,所以B1C1⊥平面A1AMN.所以平面A1AMN⊥平面EB1C1F.(2)解由已知得AM⊥BC.以M为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系M-xyz,则AB=2,AM=.连接NP,则四边形AONP为平行四边形,故PM=,E,0.由(1)知平面A1AMN⊥平面ABC,且交线为AM.作NQ⊥AM,垂足为Q,则NQ⊥平面ABC.设Q(a,0,0),则NQ=,B1,故=-a,-,-,||=.又n=(0,-1,0)是平面A1AMN的法向量,故sin=cos<n,>=.所以直线B1E与平面A1AMN所成角的正弦值为.7.(1)证明如图,以A为原点,AB,AD,AA1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,则A(0,0,0),A1(0,0,2),B(2,0,0),C(2,2,0),D(0,2,0),C1(2,2,2),D1(0,2,2).因为E为棱BC的中点,F为棱CD的中点,所以E(2,1,0),F(1,2,0),所以=(1,0,-2),=(2,2,0),=(2,1,-2).设平面A1EC1的法向量为m=(x1,y1,z1),则令x1=2,则m=(2,-2,1).因为·m=2-2=0,所以⊥m,又因为D1F⊄平面A1EC1,所以D1F∥平面A1EC1.(2)解由(1)得,=(2,2,2),设直线AC1与平面A1EC1所成角为θ,则sinθ=|cos<m,>|=.(3)解由正方体的特征可得,平面AA1C1的一个法向量为=(2,-2,0),则cos<,m>=,所以二面角A-A1C1-E的正弦值为.8.解如图,以A为原点建立空间直角坐标系,依题意可得A(0,0,0),B(0,1,0),C(2,0,0),D(1,-2,0),A1(0,0,2),B1(0,1,2),C1(2,0,2),D1(1,-2,2).又因为M,N分别为B1C和D1D的中点,得M,N(1,-2,1).(1)证明:依题意,可得n=(0,0,1)为平面ABCD的一个法向量..由此可得·n=0,又因为直线MN⊄平面ABCD,所以MN∥平面ABCD.(2)=(1,-2,2),=(2,0,0).设n1=(x1,y1,z1)为平面ACD1的法向量,则即不妨设z1=1,可得n1=(0,1,1).设n2=(x2,y2,z2)为平面ACB1的法向量,则又=(0,1,2),得不妨设z2=1,可得n2=(0,-2,1).因此有cos<n1,n2>==-,于是sin<n1,n2>=.所以,二面角D1-AC-B1的正弦值为.(3)依题意,可设=λ,其中λ∈[0,1],则E(0,λ,2),从而=(-1,λ+2,1).又n=(0,0,1)为平面ABCD的一个法向量,由已知,得cos<,n>=,整理得λ2+4λ-3=0,又因为λ∈[0,1],解得λ=-2.所以,线段A1E的长为-2.
相关试卷
这是一份高考数学一轮复习高考大题专项练四高考中的立体几何含解析新人教A版理,共16页。试卷主要包含了非选择题等内容,欢迎下载使用。
这是一份广西专用高考数学一轮复习大题专项练6高考中的概率统计与统计案例含解析新人教A版理,共9页。
这是一份广西专用高考数学一轮复习高考大题专项练四高考中的立体几何含解析新人教A版文,共11页。









