广西专用高考数学一轮复习第一章集合常用逻辑用语及不等式4简单的逻辑联结词全称量词与存在量词课件新人教A版理

这是一份广西专用高考数学一轮复习第一章集合常用逻辑用语及不等式4简单的逻辑联结词全称量词与存在量词课件新人教A版理，共25页。PPT课件主要包含了-2-，知识梳理，双基自测，“且”“或”“非”，-3-，-4-，∀x∈Mpx，-5-，-6-，-7-等内容，欢迎下载使用。
1.简单的逻辑联结词(1)命题中的　　　　　　　　　　　叫做逻辑联结词. (2)命题p∧q,p∨q, p的真假判断
2.全称量词和存在量词
3.全称命题和特称命题
∃x0∈M,p(x0)
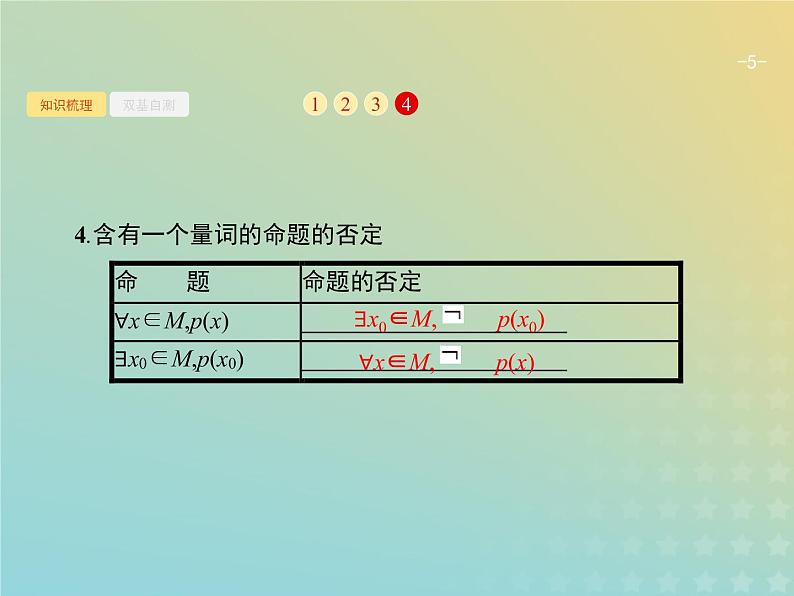
4.含有一个量词的命题的否定
∃x0∈M, p(x0)
　∀x∈M, p(x)
1.下列结论正确的打“√”,错误的打“×”.(1)若命题p∧q为假命题,则命题p,q都是假命题. (　　)(2)命题“4>6或3>2”是真命题. (　　)(3)若p∧q为真,则p∨q必为真;反之,若p∨q为真,则p∧q必为真. (　　)(4)“梯形的对角线相等”是特称命题. (　　)(5)命题“菱形的对角线相等”的否定是“菱形的对角线不相等”. (　　)
2.(2020宁夏银川四模)命题“∀x∈R,ex-x2>0”的否定是(　　)
3.命题“∃x0∈(0,+∞),ln x0=x0-1”的否定是(　　)A.∀x∈(0,+∞),ln x≠x-1B.∀x∉(0,+∞),ln x=x-1C.∃x0∈(0,+∞),ln x0≠x0-1D.∃x0∉(0,+∞),ln x0=x0-1
4.已知命题p:对任意x∈R,总有2x>0;命题q:“x>1”是“x>2”的充分不必要条件,则下列命题为真命题的是(　　)A.p∧qB.( p)∧( q)C.( p)∧qD.p∧( q)
5.(2020湖南衡阳一模)若“∃x0∈R,使得sin x0- cs x0=a”为真命题,则实数a的取值范围是(　　)A.[-2,2]B.(-2,2)C.(-∞,-2]∪[2,+∞)D.(-∞,-2)∪(2,+∞)
6.命题“所有末位数字是0的整数,都可以被5整除”的否定为　　　　　　 　　　. 
有些末位数字是0的整数,不可以被5整除
例1(1)(2017山东潍坊二模)已知命题p∧q是假命题,p∨q是真命题,则下列命题一定是真命题的是(　　)A.qB.( p)∧( q)C.pD.( p)∨( q)
(2)已知命题p:∀x>0,ln(x+1)>0;命题q:若a>b,则a2>b2,下列命题为真命题的是(　　)A.p∧qB.p∧ qC. p∧qD. p∧ q思考如何判断含简单逻辑联结词的命题的真假?
解题心得要判断一个含有逻辑联结词的命题的真假,首先判断构成这个命题的每个简单命题的真假,然后依据“p∨q见真即真”“p∧q见假即假”“p与 p真假相反”做出判断.
对点训练1(2020四川绵阳模拟)已知命题p:∃x0∈R,使得lg cs x0>0;命题q:∀x0,则下列命题为真命题的是(　　)A.p∧qB.p∨( q)C.( p)∧( q)D.p∨q
解析:命题p:∃x0∈R,使得lg cs x0>0,∵-1≤cs x≤1,∴lg cs x≤0,∴命题p为假命题.命题q:∀x0是真命题,∴p∧q为假命题,p∨( q)为假命题,( p)∧( q)为假命题,p∨q为真命题.
例2下列命题,为真命题的是(　　)B.任意x∈(0,π),sin x>cs xC.任意x∈(0,+∞),x2+1>xD.存在x0∈R, +x0=-1思考如何判断一个全称命题是真命题?又如何判断一个特称命题是真命题?
解题心得1.判定全称命题“∀x∈M,p(x)”是真命题,需要对集合M中的每个元素x,证明p(x)成立;要判断特称命题是真命题,只要在限定集合内至少能找到一个x0,使p(x0)成立.2.不管是全称命题,还是特称命题,若其真假不容易正面判断时,可先判断其否定的真假.
对点训练2(2020四川广元模拟)已知集合A={x|x2-2x≤8},B={-2, 0},下列命题为假命题的是(　　)A.∃x0∈A,x0∈BB.∃x0∈B,x0∈AC.∀x∈A,x∈BD.∀x∈B,x∈A
解析:集合A={x|x2-2x≤8}={x|-2≤x≤4}.∵B={-2,0}⊆A,∴∀x∈A,x∈B为假命题,选项A,B,D中的命题均为真命题.
例3命题“∀n∈N*,f(n)∈N*,且f(n)≤n”的否定是(　　)A.∀n∈N*,f(n)∉N*,且f(n)>nB.∀n∈N*,f(n)∉N*或f(n)>nC.∃n0∈N*,f(n0)∉N*,且f(n0)>n0D.∃n0∈N*,f(n0)∉N*或f(n0)>n0思考如何对全(特)称命题进行否定?
解题心得1.对全(特)称命题进行否定的方法是改量词,否结论.没有量词的要结合命题的含义加上量词.2.常见词语的否定形式:
A.p是假命题, p:∀x∈R,lg2(3x+1)≤0B.p是假命题, p:∀x∈R,lg2(3x+1)>0C.p是真命题, p:∀x∈R,lg2(3x+1)≤0D.p是真命题, p:∀x∈R,lg2(3x+1)>0
例4(1)已知p:∃x∈R,mx2+1≤0,q:∀x∈R,x2+mx+1>0,若p∨q为假命题,则实数m的取值范围为(　　)A.m≥2B.m≤-2C.m≤-2或m≥2D.-2≤m≤2(2)若把(1)中条件“若p∨q为假命题”改为“若p∧q为真命题”,则实数m的取值范围为　　　　　　　　. (3)若把(1)中条件“若p∨q为假命题”改为“若p∧q为假命题,p∨q为真命题”,则实数m的取值范围为　　　　　　　　　　　. 思考如何依据命题的真假求参数的取值范围?
(-∞,-2]∪[0,2)
解析: (1)由题意知p,q均为假命题.当p是假命题时,mx2+1>0恒成立,则有m≥0;当q是真命题时,有Δ=m2-4