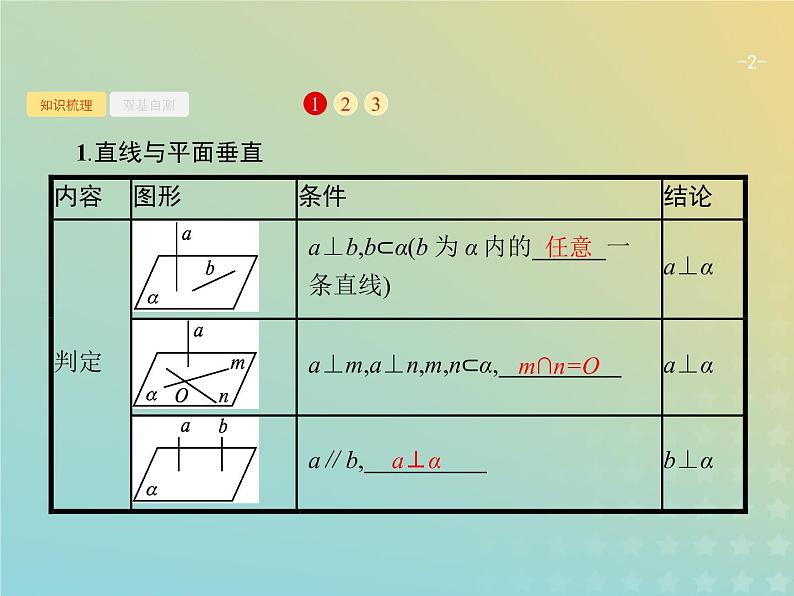
广西专用高考数学一轮复习第八章立体几何5直线平面垂直的判定与性质课件新人教A版理

这是一份广西专用高考数学一轮复习第八章立体几何5直线平面垂直的判定与性质课件新人教A版理，共37页。PPT课件主要包含了-2-，知识梳理，双基自测，直线与平面垂直，m∩nO，a⊥α，-3-，b⊂α，a∥b，-4-等内容，欢迎下载使用。

2.平面与平面垂直(1)平面与平面垂直的定义两个平面相交,如果它们所成的二面角是　　　　　　　　,就说这两个平面互相垂直. 
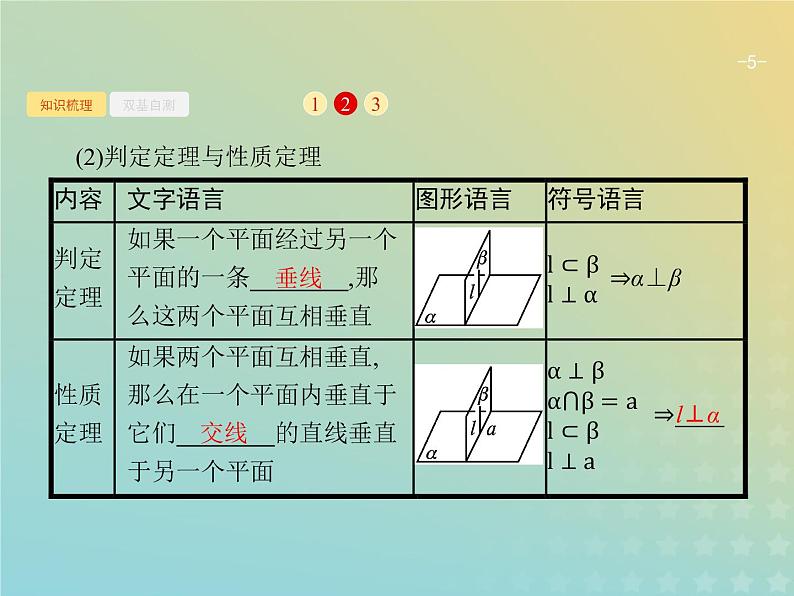
(2)判定定理与性质定理
3.常用结论(1)线面平行或垂直的有关结论①若两平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.②若一条直线垂直于一个平面,则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法).③垂直于同一条直线的两个平面平行.④一条直线垂直于两平行平面中的一个,则这一条直线与另一个平面也垂直.⑤两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.(2)证明线面垂直时,易忽视平面内两条线为相交线这一条件.
1.下列结论正确的打“√”,错误的打“×”.(1)已知直线a,b,c;若a⊥b,b⊥c,则a∥c.(　　)(2)直线l与平面α内的无数条直线都垂直,则l⊥α.(　　)(3)设m,n是两条不同的直线,α是一个平面,若m∥n,m⊥α,则n⊥α.(　　)(4)若两平面垂直,则其中一个平面内的任意一条直线垂直于另一个平面.(　　)(5)若平面α内的一条直线垂直于平面β内的无数条直线,则α⊥β.(　　)
2.若l,m为两条不同的直线,α为平面,且l⊥α,则“m∥α”是“m⊥l”的(　　)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
3.将图①中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体A-BCD(如图②),则在空间四面体A-BCD中,AD与BC的位置关系是(　　)A.相交且垂直B.相交但不垂直C.异面且垂直D.异面但不垂直
4.P为△ABC所在平面外一点,O为P在平面ABC内的射影.(1)若P到△ABC三边距离相等,且O在△ABC的内部,则O是△ABC的　　　　　心; (2)若PA⊥BC,PB⊥AC,则O是△ABC的　　　　　心; (3)若PA,PB,PC与底面所成的角相等,则O是△ABC的　　　　　心. 
5.如图,PA⊥☉O所在平面,AB是☉O的直径,C是☉O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的序号是　　　　　　　　. 
例1(2020广西玉林一模)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD,∠ABC=45°.(1)证明:AC⊥PB;
(1)证明:∵AD⊥CD,且AD=CD,∴∠ACD=∠DAC=45°.∵AD∥BC,∴∠BCA=45°,又∠ABC=45°,∴∠BAC=90°,即AC⊥AB.∵PA⊥平面ABCD,AC⊂平面ABCD,∴PA⊥AC.∵PA∩AB=A,∴AC⊥平面PAB.∵PB⊂平面PAB,∴AC⊥PB.
解题心得1.证明线面垂直的方法(1)线面垂直的判定定理(常用方法):l⊥a,l⊥b,a⊂α,b⊂α,a∩b=P⇒l⊥α.(2)面面垂直的性质定理(常用方法):α⊥β,α∩β=l,a⊂α,a⊥l⇒a⊥β.(3)性质:①a∥b,b⊥α⇒a⊥α,②α∥β,a⊥β⇒a⊥α.(4)α⊥γ,β⊥γ,α∩β=l⇒l⊥γ.(客观题可用)2.在证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形(或给出线段长度,经计算满足勾股定理)、直角梯形等等.
对点训练1如图,在正方体ABCD-A1B1C1D1中,EF⊥A1D,EF⊥AC,求证:EF∥BD1.
证明:如图,连接A1C1,C1D,B1D1,BD.因为AC∥A1C1,EF⊥AC,所以EF⊥A1C1.又EF⊥A1D,A1D∩A1C1=A1,所以EF⊥平面A1C1D.①因为BB1⊥平面A1B1C1D1,A1C1⊂平面A1B1C1D1,所以BB1⊥A1C1.因为四边形A1B1C1D1为正方形,所以A1C1⊥B1D1.又B1D1∩BB1=B1,所以A1C1⊥平面BB1D1D.又BD1⊂平面BB1D1D,所以A1C1⊥BD1.同理,DC1⊥BD1.因为DC1∩A1C1=C1,所以BD1⊥平面A1C1D.②由①②可知EF∥BD1.
例2(2020广西南宁二模)如图,在四棱锥S-ABCD中,四边形ABCD是等腰梯形,AD∥BC,AD=DC,∠ADC=120°,三角形SAB是等边三角形,平面SAB⊥平面ABCD,E,F分别为AB,AD的中点.(1)求证:平面SCD⊥平面SEF;
(1)证明:由题意知SE⊥AB.∵平面SAB⊥平面ABCD,平面SAB∩平面ABCD=AB,SE⊂平面SAB,∴SE⊥平面ABCD.又CD⊂平面ABCD,∴SE⊥CD.连接BD,∵E,F分别为AB,AD的中点,∴BD∥EF.∵AD=DC=AB,∴∠ABD=∠ADB.又∠BAD=∠ADC=120°,∴∠ADB=30°.∴∠BDC=90°,即BD⊥CD.又BD∥EF,∴CD⊥EF.又SE∩EF=E,∴CD⊥平面SEF.又CD⊂平面SCD,∴平面SCD⊥平面SEF.
(2)解:记△CDF在DF边上的高为h1,△BEC在BC边上的高为h2.则h1∶h2=CD∶BE=2∶1.在等腰梯形ABCD中,AD=DC,∠ADC=120°,可得BC=2AD=4DF,
解题心得1.两个平面互相垂直是两个平面相交的特殊情形.2.由平面和平面垂直的判定定理可知,要证明平面与平面垂直,可转化为从现有直线中寻找平面的垂线,即证明线面垂直.3.平面和平面垂直的判定定理的两个条件:l⊂α,l⊥β,缺一不可.
对点训练2如图,在三棱锥P-ABC中,平面PAB⊥平面PAC,AB⊥BP,M,N分别为PA,AB的中点.(1)求证:PB∥平面CMN;(2)若AC=PC,求证:AB⊥平面CMN.
证明:(1)在平面PAB中,因为M,N分别为PA,AB的中点,所以MN∥PB.又PB⊄平面CMN,MN⊂平面CMN,所以PB∥平面CMN.(2)在平面PAB中,因为AB⊥BP,MN∥PB,所以AB⊥MN.因为AC=PC,M为PA的中点,所以CM⊥PA.又平面PAB⊥平面PAC,平面PAB∩平面PAC=PA,所以CM⊥平面PAB.因为AB⊂平面PAB,所以CM⊥AB.又CM∩MN=M,CM⊂平面CMN,MN⊂平面CMN,所以AB⊥平面CMN.
考向一　平行与垂直关系的证明例3如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:(1)A1B1∥平面DEC1;(2)BE⊥C1E.思考处理平行与垂直关系的综合问题的主要数学思想是什么?
证明:(1)因为D,E分别为BC,AC的中点,所以ED∥AB.在直三棱柱ABC-A1B1C1中,AB∥A1B1,所以A1B1∥ED.又因为ED⊂平面DEC1,A1B1⊄平面DEC1,所以A1B1∥平面DEC1.
(2)因为AB=BC,E为AC的中点,所以BE⊥AC.因为三棱柱ABC-A1B1C1是直棱柱,所以C1C⊥平面ABC.又因为BE⊂平面ABC,所以C1C⊥BE.因为C1C⊂平面A1ACC1,AC⊂平面A1ACC1,C1C∩AC=C,所以BE⊥平面A1ACC1.因为C1E⊂平面A1ACC1,所以BE⊥C1E.
考向二　探索性问题中的平行与垂直关系例4如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°, PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且 点F为PD中点.(1)若k= ,求证:直线AF∥平面PEC;(2)是否存在一个常数k,使得平面PED⊥平面PAB?若存在,求出k的值;若不存在,请说明理由.思考探索性问题的一般处理方法是什么?
∴四边形AEMF为平行四边形.∴AF∥EM.∵AF⊄平面PEC,EM⊂平面PEC,∴直线AF∥平面PEC.
又∵∠DAB=45°,AD=1,∴AB⊥DE.又∵PD⊥平面ABCD,∴PD⊥AB.又∵PD∩DE=D,∴AB⊥平面PDE.∵AB⊂平面PAB,∴平面PED⊥平面PAB.
考向三　折叠问题中的平行与垂直关系例5如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D'EF的位置.(1)证明:AC⊥HD';思考折叠问题的处理关键是什么?
由此得EF⊥HD.又DE=DF,所以H为EF的中点.由折叠的性质知,D'E=D'F,所以EF⊥HD',所以AC⊥HD'.
故OD'⊥OH.由(1)知AC⊥HD',又AC⊥BD,BD∩HD'=H,所以AC⊥平面BHD',于是AC⊥OD'.又AC∩OH=O,AC,OH⊂平面ABC,所以OD'⊥平面ABC.
解题心得平行与垂直的综合应用问题的主要数学思想和处理策略:(1)处理平行与垂直的综合问题的主要数学思想是转化,要熟练掌握线线、线面、面面之间的平行与垂直的转化.(2)探索性问题一般是先根据条件猜测点的位置再给出证明,探索点的存在问题,点多为中点或三等分点中的某一个,也可以根据相似知识找点.(3)折叠问题中的平行与垂直关系的处理关键是结合图形弄清折叠前后变与不变的数量关系,尤其是隐含着的垂直关系.
对点训练3(1)如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2,DA= .
(2)如图①,在Rt△ABC中,∠ABC=90°,D为AC的中点,AE⊥BD于点E(不同于点D),延长AE交BC于点F,将△ABD沿BD折起,得到三棱锥A1-BCD,如图②所示.①若M是FC的中点,求证:直线DM∥平面A1EF;②求证:BD⊥A1F.
∴BD=DC=2,∵E为BC的中点,∴BC⊥DE,∵PD⊥平面ABCD,∴BC⊥PD,∵DE∩PD=D,∴BC⊥平面PDE,∵BC⊂平面PBC,∴平面PBC⊥平面PDE.