广西专用高考数学一轮复习第十章算法初步统计与统计案例3用样本估计总体课件新人教A版理

这是一份广西专用高考数学一轮复习第十章算法初步统计与统计案例3用样本估计总体课件新人教A版理，共32页。PPT课件主要包含了-2-，知识梳理，双基自测，频率fi，求极差，将数据分组，-3-，-4-，-5-，-6-等内容，欢迎下载使用。
1.用样本的频率分布估计总体分布(1)频率分布表:把反映总体频率分布的表格称为频率分布表.(2)频率分布直方图①含义:频率分布直方图由一些小矩形来表示,每个小矩形的宽度为　　　　　　　　　　　　　,高为 ,小矩形的面积恰为相应的　　　　　　,图中所有小矩形的面积之和为　　. ②绘制频率分布直方图的步骤为:a.　　　　　　;b.决定组距与组数;c.　　　　　　　　　;d.列频率分布表;e.画频率分布直方图. 
Δxi(分组的宽度)　
(3)总体密度曲线①频率分布折线图:连接频率分布直方图中各小长方形上端的中点,就得到频率分布折线图.②总体密度曲线:随着样本容量的增加,作图时所分的组数增加,组距减小,相应的频率分布折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.总体密度曲线反映了总体在各个范围内取值的百分比,它能提供更加精细的信息.(4)茎叶图:茎叶图中茎是指　　　　的一列数,叶是从茎的_____　　　　生长出来的数.当样本数据较少时,用茎叶图表示数据的效果较好,它不但可以保留所有信息,而且可以随时记录,给数据的记录和表示都带来方便. 
1.下列结论正确的打“√”,错误的打“×”.(1)平均数、众数与中位数都可以描述数据的集中趋势.(　　)(2)一组数据的方差越大,说明这组数据的波动越大.(　　)(3)在频率分布直方图中,小矩形的面积越大,表示样本数据落在该区间内的频率越大.(　　)(4)茎叶图中的数据要按从小到大的顺序写,相同的数据可以只记一次.(　　)(5)频率分布表和频率分布直方图是一组数据频率分布的两种形式,前者准确,后者直观.(　　)(6)在频率分布直方图中,最高的小长方形底边中点的横坐标是众数.(　　)
2.(2020广西桂林二模)某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为(　　)A.8B.7C.9D.168
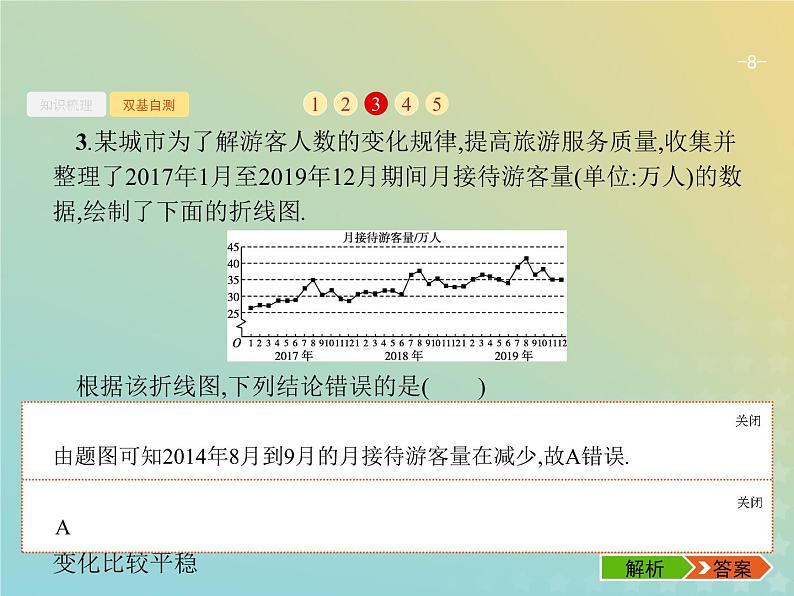
3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是(　　)A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
4.若样本数据x1,x2,…,x10的标准差为8,则数据2x1-1,2x2-1,…,2x10-1的标准差为(　　)A.8B.15 C.16 D.32
5.为了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有　　　　　株树木的底部周长小于100 cm. 
例1(1)(2020湖北武汉模拟)节约用水是中华民族的传统美德,某市政府希望在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过x的部分按平价收费,超过x的部分按议价收费.为此希望已经学习过统计的小明来给出建议.为了解全市居民用水量的分布情况,小明通过随机走访,获得了100位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了频率分布直方图如图所示.若该市政府希望使85%的居民每月的用水量不超过标准x(吨),如果你是小明,你觉得x的估计值为　　　　　.(精确到小数点后1位) 
(2)为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下频率分布直方图:
乙离子残留百分比直方图记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据频率分布直方图得到P(C)的估计值为0.70.①求乙离子残留百分比频率分布直方图中a,b的值;②分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).思考频率分布直方图有哪些性质?如何利用频率分布直方图求众数、中位数与平均数?
(1)解析:由频率分布直方图,知(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5=1,解得a=0.30.计算月均用水量小于2.5吨的居民人数所占的百分比为0.5×(0.08+0.16+0.30+0.40+0.52)=0.73,即73%的居民月均用水量小于2.5吨.同理,88%的居民月均用水量小于3吨.故2.5≤x