人教版七年级下册5.1.2 垂线随堂练习题

5.1.2  垂线

第1课时  垂线

知识点1  垂直的定义

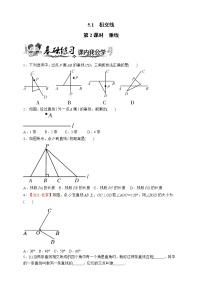
1．（2021春•兴城市期末）如图，直线AB、CD相交于点O，过O作EO⊥CD，若∠EOA＝50°，则∠BOD的度数是（　　）

A．35° B．40° C．45° D．50°

【答案】B

【解答】解：∵EO⊥CD，

∴∠EOD＝90°．

∴∠BOD＝180°﹣∠EOA﹣∠EOD＝180°﹣50°﹣90°＝40°．

故选：B．

2．（2021春•郑州期末）小红在学习垂线时遇到了这样一个问题，请你帮她解决：如图，线段AB和CD相交于点O，则下列条件中能说明AB⊥CD的是（　　）

A．AO＝OB B．CO＝OD C．∠AOC＝∠BOD D．∠AOC＝∠BOC

【答案】D

【解答】解：由OA＝OB只能得出O是AB的中点，

故A选项错误，

由OC＝OD只能得出O是CD的中点，

故B选项错误，

∠AOC和∠BOD是对顶角，始终是相等的，

故C选项错误，

∠AOC和∠BOC互补，当∠AOC＝∠BOC时，

∠AOC＝180°÷2＝90°，

∴CD⊥AB，

故选项D正确，

故选：D．

3．（2021春•老河口市期末）如图，直线AB，CD相交于点O，OE⊥CD，OF平分∠BOD，∠AOE＝24°，∠COF的度数是（　　）

A．146° B．147° C．157° D．136°

【答案】B

【解答】解：∵OE⊥CD，

∴∠EOD＝90°．

∴∠BOD＝180°﹣∠AOE﹣∠DOE＝66°．

又∵OF平分∠BOD，

∴∠DOF＝＝33°．

∴∠COF＝180°﹣∠DOF＝180°﹣33°＝147°．

故选：B．

4．（2021•河南模拟）如图，直线AB，CD相交于点O，OE⊥AB，∠DOB＝34°，则∠COE＝　  　°．

【答案】56

【解答】解：∵OE⊥AB于O，

∴∠AOE＝90°，

∵∠DOB＝24°，

∴∠AOC＝∠BOD＝34°（对顶角相等）．

∴∠COE＝∠AOE﹣∠AOC＝90°﹣34°＝56°，

故答案为：56．

5．（2021春•亳州期末）如图，AC⊥BC，直线EF经过点C，若∠1＝37°，则∠2的度数是 　    　．

【答案】53°

【解答】解：∵AC⊥BC，

∴∠ACB＝90°，

∵∠1+∠ACB+∠2＝180°，

∴∠2＝180°﹣90°﹣37°＝53°，

故答案为：53°．

考点2  垂线的画法

6．（2021秋•双阳区期末）下列各图中，过直线l外点P画l的垂线CD，三角板操作正确的是（　　）

A． B． 

C． D．

【答案】D

【解答】解：根据分析可得D的画法正确，

故选：D．

7．（2017春•文登区期中）如图，已知钝角∠AOB，点D在射线OB上．

（1）画直线DE⊥OB；

（2）画直线DF⊥OA，垂足为F．

【答案】略

【解答】解：（1）如图所示：

（2）如图所示：

考点3  垂线的性质

8．下列说法正确个数为（　　）

①过一点有且只有一条直线与已知直线垂直；

②在同一平面内，过一点有且只有一条直线与已知直线垂直；

③过直线l外一点有且只有一条直线与直线l垂直；

④过直线l上一点有且只有一条直线与已知直线l垂直．

A．1个 B．2个 C．3个 D．4个

【答案】A

【解答】解：①在同一平面内，过一点有且只有一条直线与已知直线垂直，故本小题错误；

②在同一平面内，过一点有且只有一条直线与已知直线垂直，正确；

③应为在同一平面内，过直线l外一点有且只有一条直线与直线l垂直；

④应为在同一平面内，过直线l上一点有且只有一条直线与已知直线l垂直．

综上所述，说法正确的是②共1个．

故选：A．

9．如图，直线a，b相交于点O，射线c⊥a，垂足为点O，若∠1＝40°，则∠2的度数为（　　）

A．50° B．120° C．130° D．140°

【答案】C

【解答】解：∵c⊥a，

∴∠AOB＝90°，

∵∠1＝40°，

∴∠AOC＝90°+40°＝130°，

∵∠2＝∠AOC，

∴∠2＝130°．

故选：C．

10．（2021春•金州区月考）如图，AB⊥CD于D，DE⊥DF，若∠BDE＝60°，则∠ADF的度数是（　　）

A．30° B．45° C．60° D．120°

【答案】A

【解答】解：∵DE⊥DF，

∴∠EDF＝90°，

∵∠ADF+∠EDF+∠BDE＝180°，

∴∠ADF＝180°﹣90°﹣60°＝30°，

故选：A．

11．（2020秋•虎林市期末）如图，将一副三角尺的直角顶点重合放置于点A处，下列结论：

①∠BAE＞∠DAC；②∠BAD＝∠EAC；③AD⊥BC；④∠BAE+∠DAC＝180°；⑤∠E+∠D＝∠B+∠C．其中结论正确的个数是（　　）

A．2个 B．3个 C．4个 D．5个

【答案】C

【解答】解：（1）由图可得：∠BAE＝∠CAE+∠BAD+∠CAD．

∴∠BAE＞∠DAC．

故①正确．

（2）由题意得：∠EAD＝90°，∠BAC＝90°．

∴∠EAC+∠CAD＝∠CAD+∠BAD．

∴∠EAC＝∠BAD．

故②正确．

（3）欲证AD⊥BC，需证∠B+∠DAB＝90°．

由题得：∠B＝45°．

∵题目已知条件无法证得∠DAB＝45°．

故③无法得证．

（4）由题意得：∠EAD＝90°，∠BAC＝90°．

∴∠EAC+∠CAD＝∠CAD+∠BAD＝90°．

∴∠BAE+∠DAC＝∠BAC+∠EAC+∠DAC＝90°+∠EAD＝90°+90°＝180°．

故④正确．

（5）由题意得：∠EAD＝90°，∠BAC＝90°．

∴∠E+∠D＝180﹣∠EAD＝90°，∠B+∠C＝180°﹣∠BAC＝90°．

∴∠E+∠D＝∠B+∠C．

故⑤正确．

综上：正确有①②④⑤，共4个．

故选：C．

12．（2019春•云冈区期末）如图，点O是直线AB上一点，OC⊥OD，∠AOC：∠BOD＝5：1，那么∠AOC的度数是　      　．

【答案】75°

【解答】解：∵OC⊥OD，

∴∠COD＝90°．

∴∠AOC+∠BOD＝90°

设∠BOD为x，则∠AOC为5x．

根据题意得：x+5x＝90°．

解得：x＝15°．

∴∠AOC＝5x＝75°．

故答案为：75°．

13．（2020秋•盘龙区期末）如图，已知直线AB、CD相交于点O，射线OD平分∠BOF，OE⊥CD于点O，∠AOC＝30°．

（1）求∠EOF的度数；

（2）试判断射线OE是否平分∠AOF，并说明理由．

【答案】（1） ∠EOF＝60°  （2）OE平分∠AOF

【解答】解：（1）∵OD平分∠BOF，

∴∠BOD＝∠DOF，

∵∠BOD＝∠AOC＝30°，

∴∠DOF＝30°，

∵EO⊥CD，

∴∠EOD＝90°，

∴∠EOF＝90°﹣∠DOF＝60°．

（2）OE平分∠AOF．

理由：∵∠AOB＝180°，∠EOD＝90°，

∴∠AOE+∠BOD＝90°，

∵∠BOD＝30°，

∴∠AOE＝60°，

∵∠EOF＝60°，

∴∠AOE＝∠EOF，

∴OE平分∠AOF．

14．（2020秋•永嘉县校级期末）直线AB与直线CD相交于点O，OE平分∠BOD．

（1）如图①，若∠BOC＝130°，求∠AOE的度数；

（2）如图②，射线OF在∠AOD内部．

①若OF⊥OE，判断OF是否为∠AOD的平分线，并说明理由；

②若OF平分∠AOE，∠AOF＝∠DOF，求∠BOD的度数．

【答案】（1） ∠AOE的度数为155°  （2）∠BOD的度数为60°

【解答】解：（1）∵∠BOC＝130°，

∴∠AOD＝∠BOC＝150°，

∠BOD＝180°﹣∠BOC＝50°

∵OE平分∠BOD，

∴∠DOE＝25°

∴∠AOE＝∠AOD+∠DOE＝155°．

答：∠AOE的度数为155°

（2）①OF是∠AOD的平分线，理由如下：

∵OF⊥OE，

∴∠EOF＝90°

∴∠BOE+∠AOF＝90°

∵OE平分∠BOD，

∴∠BOE＝∠DOE

∴∠DOE+∠AOF＝90°

∠DOE+∠DOF＝90°

∴∠AOF＝∠DOF

∴OF是∠AOD的平分线；

②∵∠AOF＝∠DOF，

设∠DOF＝3x，则∠AOF＝∠5x，

∵OF平分∠AOE，

∴∠AOF＝∠EOF＝5x

∴∠DOE＝2x

∵OE平分∠BOD，

∴∠BOD＝4x

5x+3x+4x＝180°

∴x＝15°．

∴∠BOD＝4x＝60°．

答：∠BOD的度数为60°．

15．（2020秋•惠城区期末）如图，直线AB与CD相交于点O，OE是∠COB的平分线，OE⊥OF．

（1）图中∠BOE的补角是 　　；

（2）若∠COF＝2∠COE，求∠BOE的度数；

（3）试判断OF是否平分∠AOC，并说明理由．

【答案】（1） ∠AOE或∠DOE   （2）∠BOE＝30°   （3），OF平分∠AOC

【解答】解：（1）∵∠AOE+∠BOE＝∠AOB＝180°，∠COE+∠DOE＝∠COD＝180°，∠COE＝∠BOE

∴∠BOE的补角是∠AOE，∠DOE

故答案为：∠AOE或∠DOE；

（2）∵OE⊥OF．∠COF＝2∠COE，

∴∠COF＝×90°＝60°，∠COE＝×90°＝30°，

∵OE是∠COB的平分线，

∴∠BOE＝∠COE＝30°；

（3）OF平分∠AOC，

∵OE是∠COB的平分线，OE⊥OF．

∴∠BOE＝∠COE，∠COE+∠COF＝90°，

∵∠BOE+∠EOC+∠COF+∠FOA＝180°，

∴∠COE+∠FOA＝90°，

∴∠FOA＝∠COF，

即，OF平分∠AOC．

  第2课时  垂线段

考点1  垂线段的定义及性质

1．（2020秋•奉化区校级期末）下列生活实例中，数学原理解释错误的一项是（　　）

A．从一条河向一个村庄引一条最短的水渠，其中数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线             

B．两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短 

C．把一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线 

D．从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连接直线外一点与直线上各点的所有线段中，垂线段最短

【答案】A

【解答】解：A、从一条河向一个村庄引一条最短的水渠，其中数学原理是：垂线段最短，故原命题错误；

B、两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短，正确；

C、一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线，正确；

D、从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连接直线外一点与直线上各点的所有线段中，垂线段最短，正确．

故选：A．

2．（2021春•当涂县期末）如图，AC⊥BC于点C，D是线段BC上任意一点，AC＝4，则AD的长不可能是（　　）

A． B．4 C．5 D．10

【答案】A

【解答】解：∵AC＝4，AC⊥BC于点C，

∴AD≥4，

∵＜4，

∴AD的长不可能是．

故选：A．

3．（2021春•香洲区期末）在乡村振兴活动中，某村通过铺设水管将河水引到村庄C处，为节省材料，他们过点C向河岸l作垂线，垂足为点D，于是确定沿CD铺设水管，这样做的数学道理是（　　）

A．两点之间，线段最短 

B．过一点有且只有一条直线与已知直线垂直 

C．垂线段最短 

D．两条直线相交有且只有一个交点

【答案】C

【解答】解：因为CD⊥l于点D，根据垂线段最短，所以CD为C点到河岸l的最短路径．故选：C．

考点2  点到直线的距离

4．（2020秋•肇源县期末）如图，点P是直线a外一点，A，B，C，D都在直线上，PB⊥α于B，下列线段最短的是（　　）

A．PA B．PC C．PB D．PD

【答案】C

【解答】解：由题意，得

点P是直线a外一点，A，B，C，D都在直线上，PB⊥α于B，下列线段最短的是PB，

故选：C．

5．（2020春•汉阳区校级期中）P是直线l外一点，A、B、C分别是l上三点，已知PA＝1，PB＝2，PC＝3，则点P到l的距离是（　　）

A．1 B．2 

C．3 D．小于或等于1

【答案】D

【解答】解：∵直线外一点与直线上各点连接的所有线段中，垂线段最短，

∴点P到直线l的距离≤PA，

即点P到直线l的距离不大于1．

故选：D．

6．（2020•高阳县模拟）如图，已知AB⊥BC，垂足为B，AB＝3，点P是射线BC上的动点，则线段AP长不可能是（　　）

A．2.5 B．3 C．4 D．5

【答案】A

【解答】解：∵AB⊥BC，

∴AP≥AB，

即AP≥3．

故选：A．

7．（2021春•罗湖区校级期末）点P是直线l外一点，A、B、C为直线l上的三点，PA＝4cm，PB＝5cm，PC＝2cm，则点P到直线l的距离（　　）

A．小于2cm B．等于2cm C．不大于2cm D．等于4cm

【答案】C

【解答】解：∵根据点到直线的距离为点到直线的垂线段（垂线段最短），

2＜4＜5，

∴点P到直线l的距离小于等于2，即不大于2，

故选：C．

8．（2019秋•侯马市期末）如图，点P，点Q分别代表两个村庄，直线l代表两个村庄中间的一条公路．根据居民出行的需要，计划在公路l上的某处设置一个公交站．

（1）若考虑到村庄P居住的老年人较多，计划建一个离村庄P最近的车站，请在公路l上画出车站的位置（用点M表示），依据是　　                             ；

（2）若考虑到修路的费用问题，希望车站的位置到村庄P和村庄Q的距离之和最小，请在公路l上画出车站的位置（用点N表示），依据是　　．

【答案】（1）直线外一点与直线上各点连接的所有线段中垂线段最短  

（2）两点之间线段最短

【解答】解：（1）如图，点M即为所示．依据是直线外一点与直线上各点连接的所有线段中垂线段最短

（2）如图，点N即为所示．依据是两点之间线段最短；

故答案为：直线外一点与直线上各点连接的所有线段中垂线段最短；两点之间线段最短．