高考数学二轮复习综合练习题1含答案

这是一份高考数学二轮复习综合练习题1含答案，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．已知集合M＝{x|y＝ln(x-1)}，N＝{x|2x-x2＞0}，则M∩N＝( D )
A．(0，＋∞)B．(2，＋∞)
C．(0，1)D．(1，2)
【解析】 ∵M＝{x|x＞1}，N＝{x|0＜x＜2}，
∴M∩N＝(1，2)．故选D.
2．若复数z满足(1＋2i)z＝(1-i)，则|z|＝( C )
A．eq \f(2,5)B．eq \f(3,5)
C．eq \f(\r(10),5)D．eq \r(10)
【解析】 由(1＋2i)z＝(1-i)，
得z＝eq \f(1-i,1＋2i)＝eq \f(（1-i）（1-2i）,（1＋2i）（1-2i）)＝eq \f(-1-3i,5)＝-eq \f(1,5)-eq \f(3,5)i，
则|z|＝eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,5)))\s\up12(2)＋\b\lc\(\rc\)(\a\vs4\al\c1(-\f(3,5)))\s\up12(2))＝eq \f(\r(10),5).
故选C.
3．霍兰德职业能力测试问卷可以为大学生在择业方面提供参考，对人的能力兴趣等方面进行评估．某大学随机抽取100名学生进行霍兰德职业能力测试问卷测试，测试结果发现这100名学生的得分都在[50，100]内，按得分分成5组：[50，60)，[60，70)，[70，80)，[80，90)，[90，100]，得到如图所示的频率分布直方图，则这100名同学得分的中位数为( A )
A．72.5 B．75
C．77.5 D．80
【解析】 根据频率分布直方图可得，得分在[50，60)内的频率为0.01×10＝0.1，
得分在[60，70)内的频率为0.03×10＝0.3，
故这100名同学得分的中位数在区间[70，80)内，
设中位数为x，则有(x-70)×0.04＝0.5-0.3-0.1，
解得x＝72.5，
故这100名同学得分的中位数为72.5.
故选A．
4．已知函数f(x)＝ex＋ax2的图象在(1，f(1))处的切线斜率为e＋2，则该切线方程为( D )
A．(e＋2)x-y＋2e-1＝0B．(e＋2)x-y-2e-3＝0
C．x-(e＋2)y-1＝0D．(e＋2)x-y-1＝0
【解析】 由f(x)＝ex＋ax2的导数
f′(x)＝ex＋2ax，
可得f′(1)＝e＋2a＝e＋2，
所以a＝1，故f(1)＝e＋1，
所以切点(1，e＋1)，
所以切线方程为y-(e＋1)＝(e＋2)(x-1)，
即(e＋2)x-y-1＝0.
故选D.
5．我国古代数学名著《九章算术》中有如下问题：“今有羡除，下广六尺，上广一丈，深三尺，末广八尺，无深，袤七尺．问积几何”，羡除是一个五面体，其中三个面是梯形，另两个面是三角形，已知一个羡除的三视图如图粗线所示，其中小正方形网格的边长为1，则该羡除的表面中，三个梯形的面积之和为( C )
A．40 B．43
C．46 D．47
【解析】 几何体的直观图如图五面体，
其中平面ABCD⊥平面ABEF，
CD＝2，AB＝6，EF＝4，底面梯形是等腰梯形，高为3，
梯形ABCD的高为4，
可知：等腰梯形FECD的高为：5，
三个梯形的面积之和为：
eq \f(2＋6,2)×4＋eq \f(4＋6,2)×3＋eq \f(2＋4,2)×5＝46.
故选C.
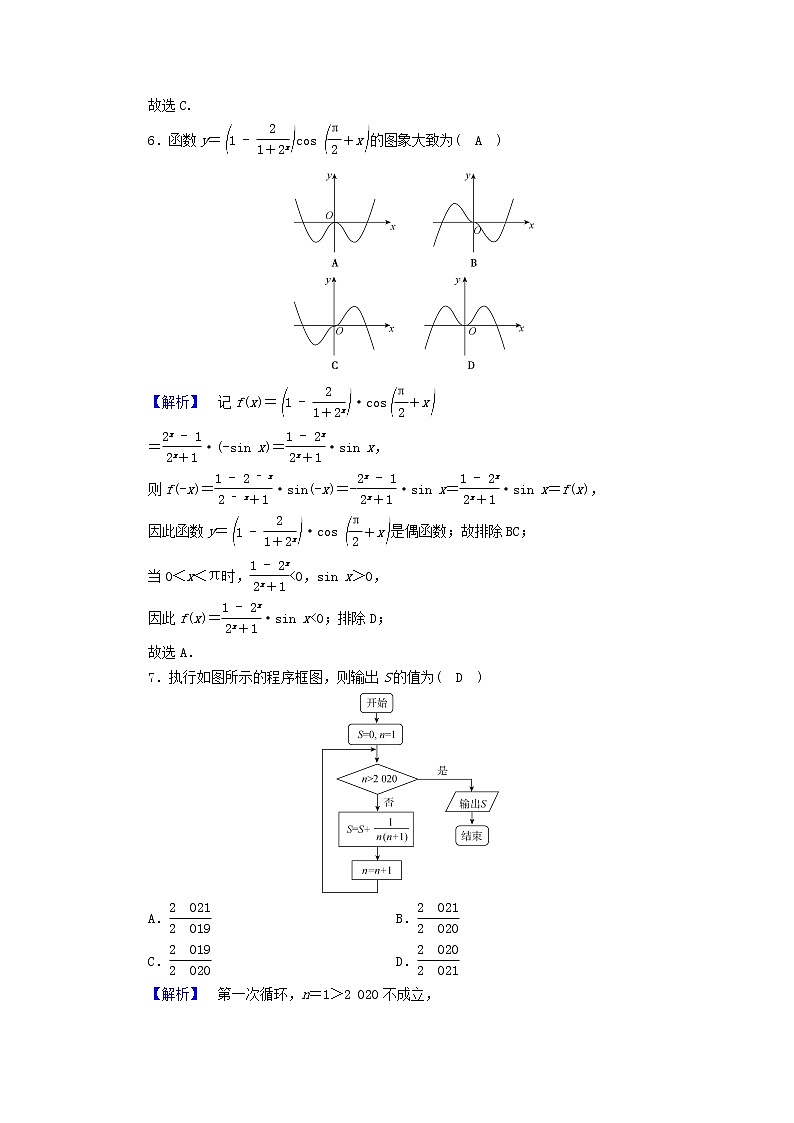
6．函数y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(2,1＋2x)))cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋x))的图象大致为( A )
【解析】 记f(x)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(2,1＋2x)))·cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋x))
＝eq \f(2x-1,2x＋1)·(-sin x)＝eq \f(1-2x,2x＋1)·sin x，
则f(-x)＝eq \f(1-2-x,2-x＋1)·sin(-x)＝-eq \f(2x-1,2x＋1)·sin x＝eq \f(1-2x,2x＋1)·sin x＝f(x)，
因此函数y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(1-\f(2,1＋2x)))·cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋x))是偶函数；故排除BC；
当0＜x＜π时，eq \f(1-2x,2x＋1)0)与抛物线y2＝x交于M，N两点，
可设M(x，eq \r(x))，N(x，-eq \r(x))，
∵△OMN的面积为2eq \r(2)，
∴xeq \r(x)＝2eq \r(2)，解得x＝2，
∴M(2，eq \r(2))，N(2，-eq \r(2))，
由已知得eq \b\lc\{(\a\vs4\al\c1(\f(c,a)＝\f(\r(2),2),\f(4,a2)＋\f(2,b2)＝1,a2＝b2＋c2))，
解得a＝2eq \r(2)，b＝c＝2.
∴椭圆C的方程为eq \f(x2,8)＋eq \f(y2,4)＝1.
(2)当直线AB的斜率不存在时，
不妨取A(2，eq \r(2))，B(2，-eq \r(2))，C(-2，-eq \r(2))，
故S△ABC＝eq \f(1,2)×2eq \r(2)×4＝4eq \r(2)；
当直线AB的斜率存在时，
设直线方程为y＝k(x-2)，
A(x1，y1)，B(x2，y2)，
联立eq \b\lc\{(\a\vs4\al\c1(y＝k（x-2）,\f(x2,8)＋\f(y2,4)＝1))，
得(1＋2k2)x2-8k2x＋8k2-8＝0.
Δ＝64k4-4(1＋2k2)(8k2-8)＝32(k2＋1)＞0.
x1＋x2＝eq \f(8k2,2k2＋1)，x1x2＝eq \f(8k2-8,2k2＋1).
|AB|＝eq \r(（1＋k2）·[（x1＋x2）2-4x1x2])
＝eq \r(（1＋k2）·\b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(\f(8k2,2k2＋1)))\s\up12(2)-4·\f(8k2-8,2k2＋1))))
＝4eq \r(2)·eq \f(k2＋1,2k2＋1).
点O到直线kx-y-2k＝0的距离
d＝eq \f(|-2k|,\r(k2＋1))＝eq \f(2|k|,\r(k2＋1))，
∵O是线段AC的中点，
∴点C到直线AB的距离为2d＝eq \f(4|k|,\r(k2＋1)).
∴S△ABC＝eq \f(1,2)|AB|·2d
＝eq \f(1,2)·eq \b\lc\(\rc\)(\a\vs4\al\c1(4\r(2)·\f(k2＋1,2k2＋1)))·eq \f(4|k|,\r(k2＋1))
＝8eq \r(2)·eq \r(\f(k2（k2＋1）,（2k2＋1）2)).
∵eq \f(k2（k2＋1）,（2k2＋1）2)＝eq \f(k2（k2＋1）,[k2＋（k2＋1）]2)
≤eq \f(k2（k2＋1）,4k2（k2＋1）2)＝eq \f(1,4)，
又k2≠k2＋1，∴等号不成立，
∴S△ABC＝8eq \r(2)·eq \r(\f(k2（k2＋1）,（2k2＋1）2))＜4eq \r(2).
综上，△ABC面积的最大值为4eq \r(2).
21．(本小题满分12分)已知函数f(x)＝eq \f(2aln x,x)＋x，g(x)＝2x-eq \f(1,x)，其中a∈R.
(1)若方程f(x)＝g(x)在[1，e](e为自然对数的底数)上存在唯一实数解，求实数a的取值范围；
(2)若存在x∈[1，e]，使不等式xf(x)>x2＋eq \f(2（a＋1）,x)＋2x成立，求实数a的取值范围．
【解析】 (1)函数f(x)＝eq \f(2aln x,x)＋x，g(x)＝2x-eq \f(1,x)，
因为f(x)＝g(x)，所以eq \f(2aln x,x)＋x＝2x-eq \f(1,x)，
即eq \f(x2,2)-aln x-eq \f(1,2)＝0，
令F(x)＝eq \f(x2,2)-aln x-eq \f(1,2)，
由题意得只需函数y＝F(x)在[1，e]上有唯一的零点，
又F′(x)＝x-eq \f(a,x)＝eq \f(x2-a,x)，其中x∈[1，e]，
①当a≤1时，F′(x)≥0恒成立，F(x)单调递增，
又F(1)＝0，则函数F(x)在区间[1，e]上有唯一的零点；
②当a≥e2时，F′(x)≤0恒成立，F(x)单调递减，
又F(1)＝0，则函数F(x)在区间[1，e]上有唯一的零点；
③当1＜a＜e2时，
当1≤x≤eq \r(a)时，F′(x)＜0，F(x)单调递减，
又F(1)＝0，所以F(eq \r(a))0)．
(1)若m＝1，求不等式f(x)＜5的解集；
(2)当函数f(x)的最小值取得最小值时，求m的值．
【解析】 (1)当m＝1时，不等式f(x)＜5，
即为|x-1|＋|x＋1|＜5.
当x＜-1时，原不等式即为-2x＜5，
解得-eq \f(5,2)