高考数学二轮复习第2篇5解析几何第1讲直线与圆课件

这是一份高考数学二轮复习第2篇5解析几何第1讲直线与圆课件，共60页。PPT课件主要包含了专题五解析几何，第一讲直线与圆，高频考点，真题热身，ACD，ABD，感悟高考，考点一直线的方程，典例1，考点二圆的方程等内容，欢迎下载使用。
导航立前沿•考点启方向
自主先热身•真题定乾坤
核心拔头筹•考点巧突破
明晰易错点•高考零失误
1．直线方程、圆的方程、两直线的平行与垂直、直线与圆的位置关系是本讲高考的重点．2．考查的主要内容包括求直线(圆)的方程、点到直线的距离、直线与圆的位置关系判断、简单的弦长与切线问题，多为选择题、填空题．
【解析】　由于圆上的点(2，1)在第一象限，若圆心不在第一象限，则圆至少与一条坐标轴相交，不合乎题意，所以圆心必在第一象限，设圆心的坐标为(a，a)，则圆的半径为a，圆的标准方程为(x-a)2＋(y-a)2＝a2.由题意可得(2-a)2＋(1-a)2＝a2，可得a2-6a＋5＝0，解得a＝1或a＝5，所以圆心的坐标为(1，1)或(5，5)，
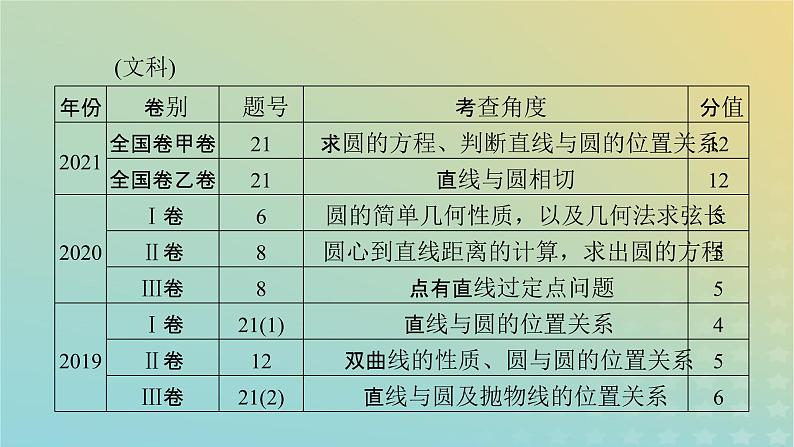
3．(2020·全国卷Ⅰ卷)已知⊙M：x2＋y2-2x-2y-2＝0，直线l：2x＋y＋2＝0，P为l上的动点，过点P作⊙M的切线PA，PB，切点为A，B，当|PM|·|AB|最小时，直线AB的方程为(　　)A．2x-y-1＝0B．2x＋y-1＝0C．2x-y＋1＝0D．2x＋y＋1＝0
5．(多选)(2021·全国新高考Ⅱ卷)已知直线l：ax＋by-r2＝0与圆C：x2＋y2＝r2，点A(a，b)，则下列说法正确的是(　　　)A．若点A在圆C上，则直线l与圆C相切B．若点A在圆C内，则直线l与圆C相离C．若点A在圆C外，则直线l与圆C相离D．若点A在直线l上，则直线l与圆C相切
6．(2018·全国卷Ⅱ)设抛物线C：y2＝4x的焦点为F，过F且斜率为k(k>0)的直线l与C交于A，B两点，|AB|＝8.(1)求l的方程；(2)求过点A，B且与C的准线相切的圆的方程．
7．(2021·全国卷甲卷)抛物线C的顶点为坐标原点O，焦点在x轴上，直线l：x＝1交C于P，Q两点，且OP⊥OQ.已知点M(2，0)，且⊙M与l相切．(1)求C，⊙M的方程；(2)设A1，A2，A3是C上的三个点，直线A1A2，A1A3均与⊙M相切．判断直线A2A3与⊙M的位置关系，并说明理由．
1．近两年圆的方程成为高考全国课标卷命题的热点，需重点关注．此类试题难度中等偏下，多以选择题或填空题形式考查．2．直线与圆的方程偶尔单独命题，单独命题时有一定的深度，有时也会出现在压轴题的位置，难度较大，对直线与圆的方程(特别是直线)的考查主要体现在圆锥曲线的综合问题上．
3．两条直线平行与垂直的判定若两条不重合的直线l1，l2的斜率k1，k2存在，则l1∥l2⇔k1＝k2，l1⊥l2⇔k1k2＝-1，若给出的直线方程中存在字母系数，则要考虑斜率是否存在．
(1)(2021·辽宁高三二模)若两直线l1：(a-1)x-3y-2＝0与l2：x-(a＋1)y＋2＝0平行，则a的值为(　　)A．±2B．2　C．-2　D．0
【解析】　(1)由题意知：-(a＋1)(a-1)-(-3)×1＝0，整理得4-a2＝0，∴a＝±2，故选A．
(2)(2021·全国高三模拟)已知直线l1：a2x＋y-2＝0与直线l2：x-(2a＋3)y＋1＝0垂直，则a＝(　　)A．3B．1或-3C．-1D．3或-1
【解析】　(2)直线l1：a2x＋y-2＝0与直线l2：x-(2a＋3)y＋1＝0垂直，所以a2-(2a＋3)＝0，解得a＝-1或a＝3.故选D.
求解直线方程应注意的问题(1)求解两条直线平行的问题时，在利用A1B2-A2B1＝0建立方程求出参数的值后，要注意代入检验，排除两条直线重合的情况．(2)要注意几种直线方程的局限性，点斜式、斜截式要求直线不能与x轴垂直；两点式要求直线不能与坐标轴垂直；截距式方程不能表示过原点的直线，也不能表示垂直于坐标轴的直线．(3)求直线方程要考虑直线的斜率是否存在．
1．(2021·北京市十一学校高三模拟)直线x＋ay＋2＝0与直线ax＋y＋2a2＝0平行，则实数a的值为(　　)A．1或-1B．0或-1C．-1D．1
1．圆的标准方程当圆心为(a，b)，半径为r时，其标准方程为(x-a)2＋(y-b)2＝r2，特别地，当圆心在原点时，方程为x2＋y2＝r2.
(1)(理)(2021·黑龙江佳木斯一中高三三模)已知圆C的圆心坐标是(0，m)，若直线2x-y＋3＝0与圆C相切于点A(2，7)，则圆C的标准方程为______________________.
x2＋(y-8)2＝5　
(2)已知两点A(2，0)，B(0，2)，则以线段AB为直径的圆的方程为____________________.
(x-1)2＋(y-1)2＝2　
求圆的方程的两种方法(1)几何法：通过已知条件，利用相应的几何知识求圆的圆心，半径．(2)代数法：用待定系数法先设出圆的方程，再由条件求得各系数．
3．在平面直角坐标系xOy中，矩形OABC的顶点坐标分别为O(0，0)，A(-4，0)，B(-4，2)，C(0，2)，则矩形OABC的外接圆方程是(　　)A．x2＋y2-4x＋2y＝0B．x2＋y2＋4x-2y＝0C．x2＋y2-8x＋4y＝0D．x2＋y2＋8x-4y＝0
4．圆C的半径为5，圆心在x轴的负半轴上，且被直线3x＋4y＋4＝0截得的弦长为6，则圆C的方程为(　　)A．x2＋y2-2x-3＝0B．x2＋16x＋y2＋39＝0C．x2-16x＋y2-39＝0D．x2＋y2-4x＝0　
1．直线与圆的位置关系的判定(1)几何法把圆心到直线的距离d和半径r的大小加以比较：d＜r⇔相交；d＝r⇔相切；d＞r⇔相离． (2)代数法将圆的方程和直线的方程联立起来组成方程组，消元后得到一元二次方程，利用判别式Δ来讨论位置关系：Δ＞0⇔相交；Δ＝0⇔相切；Δ＜0⇔相离．
考点三　直线与圆、圆与圆的位置关系
2．圆与圆的位置关系的判定(1)d＞r1＋r2⇔两圆外离；(2)d＝r1＋r2⇔两圆外切；(3)|r1-r2|＜d＜r1＋r2⇔两圆相交；(4)d＝|r1-r2|(r1≠r2)⇔两圆内切；(5)0≤d＜|r1-r2|(r1≠r2)⇔两圆内含．
1．直线(圆)与圆位置关系问题的求解思路(1)研究直线与圆的位置关系主要通过比较圆心到直线的距离和圆的半径实现，两个圆的位置关系的判断依据是两圆圆心距与两半径差与和的比较．(2)利用位置关系求过圆外一定点的切线方程的基本思路：先将直线方程设为点斜式，再利用圆心到直线的距离等于半径求斜率．
5．(2020·安徽宿州市·高二期中)圆O1：(x-1)2＋(y-2)2＝2与圆O2：x2＋y2＋4x＋2y-3＝0的位置关系是(　　)A．相离B．相交C．外切D．内切
a为何值时，(1)直线l1：x＋2ay-1＝0与直线l2：(3a-1)x-ay-1＝0平行？(2)直线l3：2x＋ay＝2与直线l4：ax＋2y＝1垂直？
易错点一：忽视对斜率为零或不存在等特殊情况的讨论致误
【易错释疑】　此题出错是因为：(1)没有考虑斜率不存在即a＝0的情况；(2)没有考虑l3的斜率不存在且l4斜率为0也符合要求这种情况．
已知圆C的方程为x2＋y2＋ax＋2y＋a2＝0，一定点为A(1，2)，且过定点A(1，2)作圆的切线有两条，求a的取值范围．
易错点二：忽视圆的一般方程中的隐含条件致误
【易错释疑】　二元二次方程x2＋y2＋Dx＋Ey＋F＝0表示圆是有条件的，必须有D2＋E2-4F>0.在解题时很容易忽视这个条件导致错误．在解决此类问题时，可以直接判断D2＋E2-4F>0，也可以配方后，判断方程右侧大于0，因为右侧相当于r2.
已知直线l与点A(3，3)和B(5，2)的距离相等，且过二直线l1：3x-y-1＝0和l2：x＋y-3＝0的交点，则直线l的方程为__________________________．
易错点三：在求直线方程时数字与代数式运算出错
x-6y＋11＝0或x＋2y-5＝0