高考数学一轮复习单元质检十算法初步统计与统计案例含解析新人教A版理

单元质检十　算法初步、统计与统计案例

(时间:45分钟　满分:100分)

一、选择题(本大题共6小题,每小题7分,共42分)

1.执行如图所示的程序框图,输出的s值为(　　)

A. B. C. D.

答案:B

解析:第一步:s=1-,k=2,k<3;

第二步:s=,k=3,输出s.

故选B.

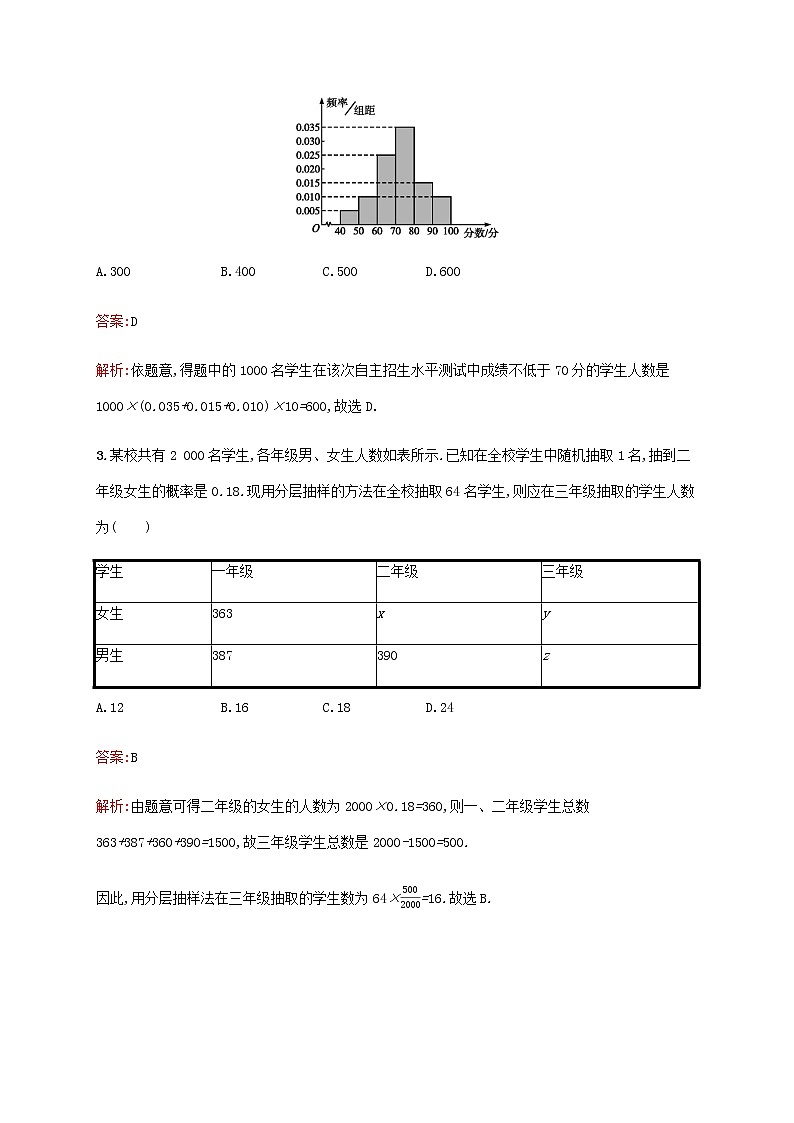
2.某大学对1 000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图如图所示,则这1 000名学生在该次自主招生水平测试中成绩不低于70分的学生人数是(　　)

A.300 B.400 C.500 D.600

答案:D

解析:依题意,得题中的1000名学生在该次自主招生水平测试中成绩不低于70分的学生人数是1000×(0.035+0.015+0.010)×10=600,故选D.

3.某校共有2 000名学生,各年级男、女生人数如表所示.已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.18.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为(　　)

A.12 B.16 C.18 D.24

答案:B

解析:由题意可得二年级的女生的人数为2000×0.18=360,则一、二年级学生总数363+387+360+390=1500,故三年级学生总数是2000-1500=500.

因此,用分层抽样法在三年级抽取的学生数为64×=16.故选B.

4.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据某地某日早7点到晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图如图所示,则甲、乙两地PM2.5的方差较小的是(　　)

A.甲 B.乙

C.甲、乙相等 D.无法确定

答案:A

解析:从茎叶图上可以观察到:甲监测点的样本数据比乙监测点的样本数据更加集中,因此甲地PM2.5的方差较小.

5.在利用最小二乘法求回归方程=0.67x+54.9时,用到了下面表中的5组数据,则表格中a的值为(　　)

A.68 B.70 C.75 D.72

答案:A

解析:由题意可得(10+20+30+40+50)=30,(62+a+75+81+89)=(a+307).

因为回归直线方程=0.67x+54.9过样本点的中心,所以(a+307)=0.67×30+54.9,解得a=68.

6.某高校进行自主招生,先从报名者中筛选出400人参加笔试,再按笔试成绩择优选出100人参加面试.现随机调查了24名笔试者的成绩,如下表所示:

据此估计允许参加面试的分数线是(　　)

A.75 B.80 C.85 D.90

答案:B

解析:因为参加笔试的400人中择优选出100人,所以每个人被择优选出的概率P=.因为随机调查24名笔试者,所以估计能够参加面试的人数为24×=6.观察表格可知,分数在[80,85)的有5人,分数在[85,90)的有1人,故面试的分数线大约为80分,故选B.

二、填空题(本大题共3小题,每小题7分,共21分)

7.若一组样本数据2,3,7,8,a的平均数为5,则该组数据的方差s2=　　　　　. 

答案:

解析:∵=5,∴a=5.

∴s2=[(2-5)2+(3-5)2+(7-5)2+(8-5)2+(5-5)2]=.

8.有24名投资者想到海南某地投资,他们年龄的茎叶图如图所示,先将他们的年龄从小到大编号为1~24号,再用系统抽样方法抽出6名投资者,邀请他们到海南某地实地考察.其中年龄不超过55岁的人数为　　　　　. 

答案:2

解析:因为系统抽样方法是等距抽样,所以从小到大每4人(一个区间)抽出一人.因为不超过55岁落在(39,40,41,41),(42,45,51,53),所以应抽取2人.

9.执行如图所示的程序框图,若输出的结果为80,则判断框内应填入　　　　　. 

答案:n>7?

解析:模拟程序的运行,可得S=0,n=1,a=3,执行循环体,S=3,a=5,

不满足条件,执行循环体,n=2;S=8,a=7,

不满足条件,执行循环体,n=3;S=15,a=9,

不满足条件,执行循环体,n=4;S=24,a=11,

不满足条件,执行循环体,n=5;S=35,a=13,

不满足条件,执行循环体,n=6;S=48,a=15,

不满足条件,执行循环体,n=7;S=63,a=17,

不满足条件,执行循环体,n=8;S=80,a=19,

由题意,此时满足条件,退出循环,输出的S结果为80,

则判断框内应填入“n>7?”.

三、解答题(本大题共3小题,共37分)

10.(12分)从某校随机抽取200名学生,获得了他们一周课外阅读时间(单位:h)的数据,整理得到数据的频数分布表和频率分布直方图(如图).

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12 h的概率;

(2)求频率分布直方图中的a,b的值;

(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.

解:(1)由频率分布表可知该周课外阅读时间不少于12h的频数为12+4+4=20,故可估计该周课外阅读时间少于12h的概率为1-=0.9.

(2)由频率分布表可知数据在[4,6)的频数为34,故这一组的频率为0.17,即a=0.085,数据在[8,10)的频数为50,故这一组的频率为0.25,即b=0.125.

(3)数据的平均数为(1×12+3×16+5×34+7×44+9×50+11×24+13×12+15×4+17×4)=7.68(h),故样本中的200名学生该周课外阅读时间的平均数在第四组.

11.(12分)某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示,其中一个数字被污损.

(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.

(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了4名观众的周均学习成语知识的时间y(单位:时)与年龄x(单位:岁),并制作了对照表(如下表所示):

由表中数据分析,x,y呈线性相关关系,试求线性回归方程x+,并预测年龄为60岁的观众周均学习成语知识的时间.

参考公式:.

解:(1)设被污损的数字为a,则a有10种情况.

令88+89+90+91+92>83+83+87+90+a+99,

则a<8,

东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数,有8种情况,所求概率为.

(2)由题意可知=35,=3.5,xiyi=525,=5400,

所以,所以x+.

当x=60时,×60+=5.25(时).

故预测年龄为60岁的观众周均学习成语知识的时间为5.25时.

12.(13分)某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:min)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60]六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40 min的学生评价为“课外体育达标”.

(1)请根据频率分布直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?

(2)现从“课外体育达标”学生中按分层抽样抽取5人,再从这5名学生中随机抽取2人参加体育知识问卷调查,求抽取的这2人课外体育锻炼时间都在[40,50)内的概率.

附参考公式与数据:K2=

解:(1)根据频率分布直方图,得“课外体育达标”的学生数为200×(0.020+0.005)×10=50.

由2×2列联表可知“课外体育达标”的男生人数为30,女生人数为20.

补全2×2列联表如下:

计算K2的观测值

k==≈6.061<6.635,

故在犯错误的概率不超过0.01的前提下不能认为“课外体育达标”与性别有关.

(2)从“课外体育达标”学生中按分层抽样抽取5人,其中课外体育锻炼时间在[40,50)内有5×=4(人),分别记为a,b,c,d;

在[50,60]上有1人,记为E.

从这5人中抽取2人,总的基本事件有ab,ac,ad,aE,bc,bd,bE,cd,cE,dE共10种,其中2人都在[40,50)内的基本事件有ab,ac,ad,bc,bd,cd共6种,故所求的概率为=0.6.