2022年河北省邯郸市中考数学三模试卷（含答案解析）

这是一份2022年河北省邯郸市中考数学三模试卷（含答案解析），共23页。试卷主要包含了5，−4C，若BC=75，则GH的长为，【答案】D，00025=2，【答案】B，【答案】C，【答案】A等内容，欢迎下载使用。
2022年河北省邯郸市中考数学三模试卷

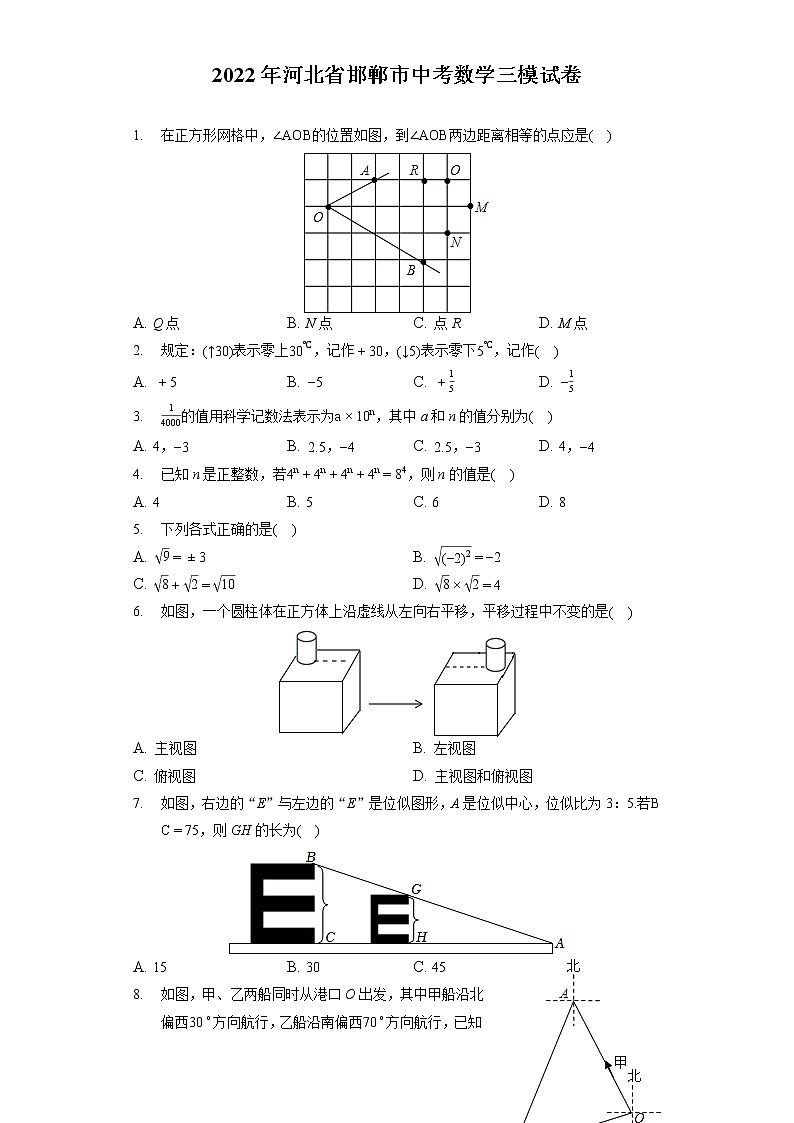
1. 在正方形网格中，∠AOB的位置如图，到∠AOB两边距离相等的点应是( )
A. Q点 B. N点 C. 点R D. M点
2. 规定：(↑30)表示零上30℃，记作+30，(↓5)表示零下5℃，记作( )
A. +5 B. −5 C. +15 D. −15
3. 14000的值用科学记数法表示为a×10n，其中a和n的值分别为( )
A. 4，−3 B. 2.5，−4 C. 2.5，−3 D. 4，−4
4. 已知n是正整数，若4n+4n+4n+4n=84，则n的值是( )
A. 4 B. 5 C. 6 D. 8
5. 下列各式正确的是( )
A. 9=±3 B. (−2)2=−2
C. 8+2=10 D. 8×2=4
6. 如图，一个圆柱体在正方体上沿虚线从左向右平移，平移过程中不变的是( )
A. 主视图 B. 左视图
C. 俯视图 D. 主视图和俯视图
7. 如图，右边的“E”与左边的“E”是位似图形，A是位似中心，位似比为3：5.若BC=75，则GH的长为( )
A. 15 B. 30 C. 45 D. 60
8. 如图，甲、乙两船同时从港口O出发，其中甲船沿北偏西30∘方向航行，乙船沿南偏西70∘方向航行，已知两船的航行速度相同，如果1小时后甲、乙两船分别到达点A、B处，那么点B位于点A的( )


A. 南偏西40∘ B. 南偏西30∘ C. 南偏西20∘ D. 南偏西10∘
9. 如图，数轴上的点A、B分别表示数1、−2x+3.则表示数−x+2的点P与线段AB的位置关系是( )
A. P在线段AB上 B. P在线段AB的延长线上
C. P在线段AB的反向延长线上 D. 不能确定
10. 某班级共有41人，在一次体质测试中，有1人未参加集体测试，老师对集体测试的成绩按40人进行了统计，得到测试成绩分数的平均数是88，中位数是85.缺席集体测试的同学后面进行了补测，成绩为88分，关于该班级41人的体质测试成绩，下列说法正确的是( )
A. 平均数不变，中位数变大 B. 平均数不变，中位数无法确定
C. 平均数变大，中位数变大 D. 平均数不变，中位数变小
11. 在证明勾股定理时，甲、乙两位同学分别设计了方案：
甲：如图，用四个全等的直角三角形拼成，其中四边形ABDE和四边形CFGH均是正方形，通过用两种方法表示正方形ABDE的面积来进行证明；
乙：两个全等的直角三角板ABC和直角三角板DEF，顶点F在BC边上，顶点C、D重合，通过用两种方法表示四边形ACBE的面积来进行证明．

对于甲、乙两种方案，下列判断正确的是( )
A. 甲、乙均对 B. 甲对、乙不对 C. 甲不对，乙对 D. 甲、乙均不对
12. 若运算的结果为整式，则“□”中的式子可能是( )
A. y−x B. y+x C. 2x D. 1x
13. 如图，直线AB，CD交于点O，若AB，CD是等边△MNP的两条对称轴，且点P在直线CD上(不与点O重合)，则点M，N中必有一个在( )

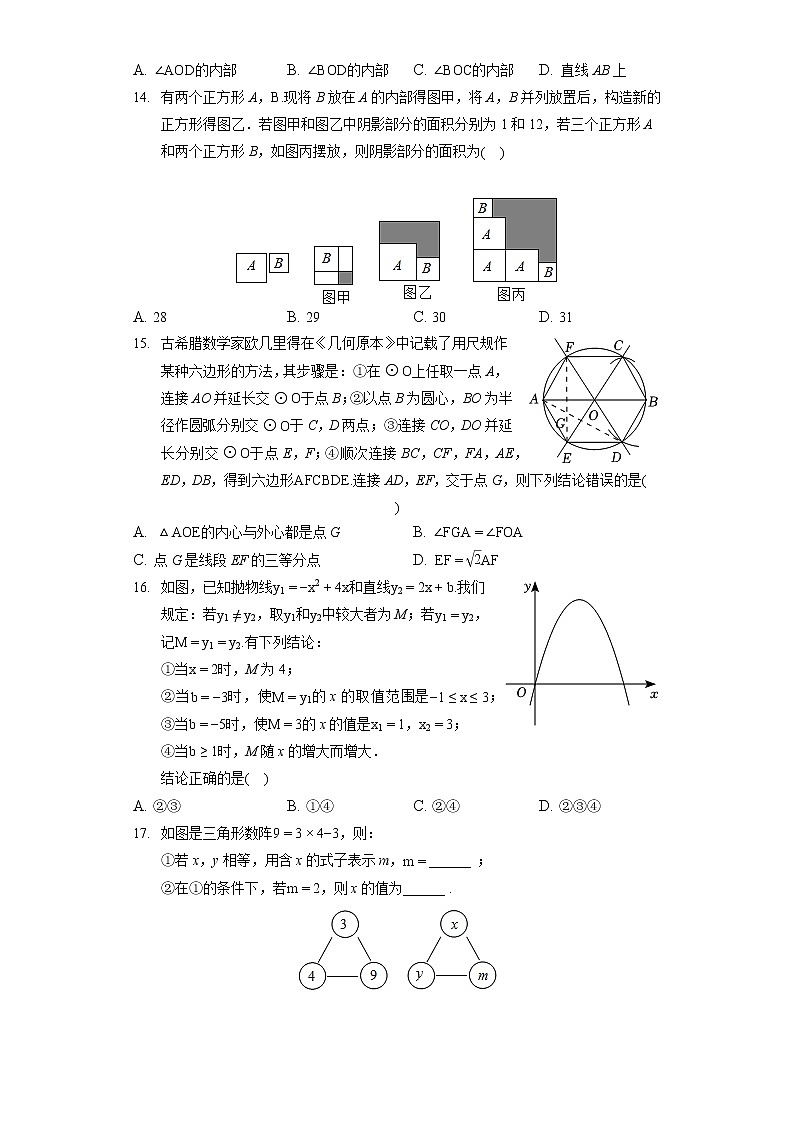
A. ∠AOD的内部 B. ∠BOD的内部 C. ∠BOC的内部 D. 直线AB上
14. 有两个正方形A，B.现将B放在A的内部得图甲，将A，B并列放置后，构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和12，若三个正方形A和两个正方形B，如图丙摆放，则阴影部分的面积为( )

A. 28 B. 29 C. 30 D. 31
15. 古希腊数学家欧几里得在《几何原本》中记载了用尺规作某种六边形的方法，其步骤是：①在⊙O上任取一点A，连接AO并延长交⊙O于点B；②以点B为圆心，BO为半径作圆弧分别交⊙O于C，D两点；③连接CO，DO并延长分别交⊙O于点E，F；④顺次连接BC，CF，FA，AE，ED，DB，得到六边形AFCBDE.连接AD，EF，交于点G，则下列结论错误的是( )
A. △AOE的内心与外心都是点G B. ∠FGA=∠FOA
C. 点G是线段EF的三等分点 D. EF=2AF
16. 如图，已知抛物线y1=−x2+4x和直线y2=2x+b.我们规定：若y1≠y2，取y1和y2中较大者为M；若y1=y2，记M=y1=y2.有下列结论：
①当x=2时，M为4；
②当b=−3时，使M=y1的x的取值范围是−1≤x≤3；
③当b=−5时，使M=3的x的值是x1=1，x2=3；
④当b≥1时，M随x的增大而增大．
结论正确的是( )
A. ②③ B. ①④ C. ②④ D. ②③④
17. 如图是三角形数阵9=3×4−3，则：
①若x，y相等，用含x的式子表示m，m=______ ；
②在①的条件下，若m=2，则x的值为______ .

18. 如图，⊙O与正五边形ABCDE的边AB，CD分别相切于点A，D.
(1)连接OA，则∠OAE的度数为______；
(2)若△ADP内接于⊙O，则∠APD的度数为______.
19. 如图，矩形ABCO在平面直角坐标系xOy中，点A(−5,0)，点C(0,6)，已知双曲线L1：y=k1x(xb)，得图甲中阴影部分的面积为(a−b)2=a²−2ab+b²=1，可解得a−b=1，图乙中阴影部分的面积为(a+b)2−(a2+b2)=2ab=12，可得(a+b)²=(a−b)²+4ab=1+2×12=25，可得a+b=5，所以图丙中阴影部分的面积为(2a+b)²−(3a²+2b²)=a²+4ab−b²=(a+b)(a−b)+4ab，代入就可计算出结果．
此题考查了灵活利用乘法公式求图形面积问题的能力，关键是能根据图形列出对应的算式．

15.【答案】D
【解析】解：在正六边形AEDBCF中，∠AOF=∠AOE=∠EOD=60∘，
∵OF=OA=OE=OD，
∴△AOF，△AOE，△EOD都是等边三角形，
∴AF=AE=OE=OF，OA=AE=ED=OD，
∴四边形AEOF，四边形AODE都是菱形，
∴AD⊥OE，EF⊥OA，
∴△AOE的内心与外心都是点G，故A正确，
∵∠EAF=120∘，∠EAD=30∘，
∴∠FAD=90∘，
∵∠AFE=30∘，
∴∠AGF=∠AOF=60∘，故B正确，
∵∠GAE=∠GEA=30∘，
∴GA=GE，
∵FG=2AG，
∴FG=2GE，
∴点G是线段F的三等分点，故C正确，
∵AF=AE，∠FAE=120∘，
∴EF=3AF，故D错误，
故选：D.
A、正确．证明△AOE是等边三角形，EF⊥OA，AD⊥OE，可得结论．
B、正确．证明∠AGF=∠AOF=60∘，可得结论．
C、正确．证明FG=2GE，可得结论．
D、错误．证明EF=3AF，可得结论．
本题考查作图-复杂作图，等边三角形的判定和性质，菱形的判定和性质，三角形的内心，外心等知识，解题的关键是证明四边形AEOF，四边形AODE都是菱形，属于中考常考题型．

16.【答案】C
【解析】解：①当x=2时，y1=4，y2=4+b，无法判断4与4+b的大小，故①错误．
②如图1中，b=−3时，

由y=−x2+4xy=2x−3，解得x=−1y=−5或x=3y=3，
∴两个函数图象的交点坐标为(−1,−5)和(3,3)，
观察图象可知，使M>y2的x的取值范围是−11时，直线y=2x+b与抛物线没有交点，由此即可判断．
本题考查二次函数的性质，一次函数的性质等知识，解题的关键是理解题意，学会用转化的思想思考问题，属于中考常考题型．

17.【答案】x2−x2或−1
【解析】解：①由数阵可知：
最上方数字×左下角数字-最上方数字=右下角数字，
因此，m=xy−x，
又x=y，
所以，m=x2−x.
②∵m=2，
∴x2−x=2.
解得：x=2或x=−1.
故答案为：①m=x2−x；②2或−1.
①根据圆圈中的数据，可以发现数字的变化特点，从而可以求得：最上方数字×左下角数字-最上方数字=右下角数字；
②代入m的值，解方程即可．
本题主要考查了规律型：数字的变化类和解一元二次方程，是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．

18.【答案】18∘72∘或108∘
【解析】解：(1)如图，连接OB，OD，
∵五边形ABCDE是正五边形，
∴∠BAE=∠CDE=180∘−360∘5=108∘.
∵AB、DE与⊙O相切，
∴∠BAO=∠ODC=90∘，
∴∠OAE=∠BAE−∠BAO=18∘，
故答案为：18∘；
(2)如图，∵五边形ABCDE是正五边形，
∴∠B=∠C=180∘−360∘5=108∘.
∵AB、DE与⊙O相切，
∴∠BAO=∠ODC=90∘，
∴∠AOD=540∘−90∘−90∘−108∘−108∘=144∘，
∴∠APD=12∠AOD=74∘，
∴∠AP′D=180∘−72∘=108∘，
故∠APD的度数为72∘或108∘，
故答案为：72∘或108∘.
(1)如图，连接OB，OD根据五边形的性质得到∠BAE=∠CDE=180∘−360∘5=108∘.根据切线的性质得到∠BAO=∠ODC=90∘，于是得到结论；
(2)根据正五边形的性质得到∠B=∠C=180∘−360∘5=108∘.根据切线的性质得到∠BAO=∠ODC=90∘，求得∠AOD=540∘−90∘−90∘−108∘−108∘=144∘，根据圆周角定理即可得到结论．
本题主要考查了切线的性质、正五边形的性质、多边形的内角和公式、熟练掌握切线的性质是解决本题的关键．

19.【答案】−6156
【解析】解：(1)∵y=k1x(x