2021-2022学年贵州省黔西南州望谟六中学初中数学毕业考试模拟冲刺卷含解析

这是一份2021-2022学年贵州省黔西南州望谟六中学初中数学毕业考试模拟冲刺卷含解析，共24页。试卷主要包含了平面直角坐标系中的点P，已知抛物线c，已知∠BAC=45等内容，欢迎下载使用。

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
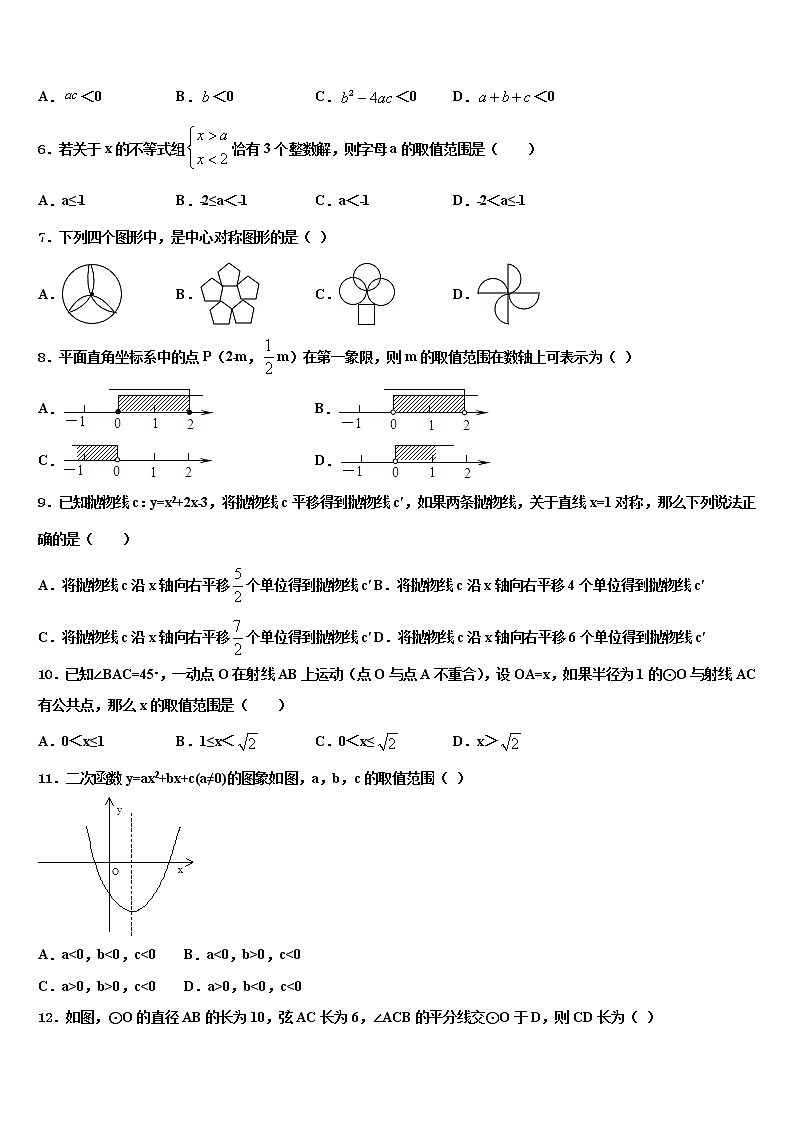
1．已知平面内不同的两点A（a+2，4）和B（3，2a+2）到x轴的距离相等，则a的值为( )
A．﹣3B．﹣5C．1或﹣3D．1或﹣5
2．化简的结果是（ ）
A．﹣ B．﹣ C．﹣ D．﹣
3．如图：将一个矩形纸片，沿着折叠，使点分别落在点处.若，则的度数为（ ）
A．B．C．D．
4．如图，点C、D是线段AB上的两点，点D是线段AC的中点．若AB=10cm，BC=4cm，则线段DB的长等于（ ）
A．2cmB．3cmC．6cmD．7cm
5．已知二次函数的图象如图所示，则下列说法正确的是（ ）
A．＜0B．＜0C．＜0D．＜0
6．若关于x的不等式组恰有3个整数解，则字母a的取值范围是（ ）
A．a≤﹣1B．﹣2≤a＜﹣1C．a＜﹣1D．﹣2＜a≤﹣1
7．下列四个图形中，是中心对称图形的是（ ）
A．B．C．D．
8．平面直角坐标系中的点P（2﹣m，m）在第一象限，则m的取值范围在数轴上可表示为（ ）
A．B．
C．D．
9．已知抛物线c：y=x2+2x﹣3，将抛物线c平移得到抛物线c′，如果两条抛物线，关于直线x=1对称，那么下列说法正确的是（ ）
A．将抛物线c沿x轴向右平移个单位得到抛物线c′B．将抛物线c沿x轴向右平移4个单位得到抛物线c′
C．将抛物线c沿x轴向右平移个单位得到抛物线c′D．将抛物线c沿x轴向右平移6个单位得到抛物线c′
10．已知∠BAC=45。，一动点O在射线AB上运动（点O与点A不重合），设OA=x，如果半径为1的⊙O与射线AC有公共点，那么x的取值范围是（ ）
A．0＜x≤1B．1≤x＜C．0＜x≤D．x＞
11．二次函数y=ax2+bx+c(a≠0)的图象如图，a，b，c的取值范围（ ）
A．a<0，b<0，c<0 B．a<0，b>0，c<0
C．a>0，b>0，c<0 D．a>0，b<0，c<0
12．如图，⊙O的直径AB的长为10，弦AC长为6，∠ACB的平分线交⊙O于D，则CD长为（ ）
A．7B．C．D．9
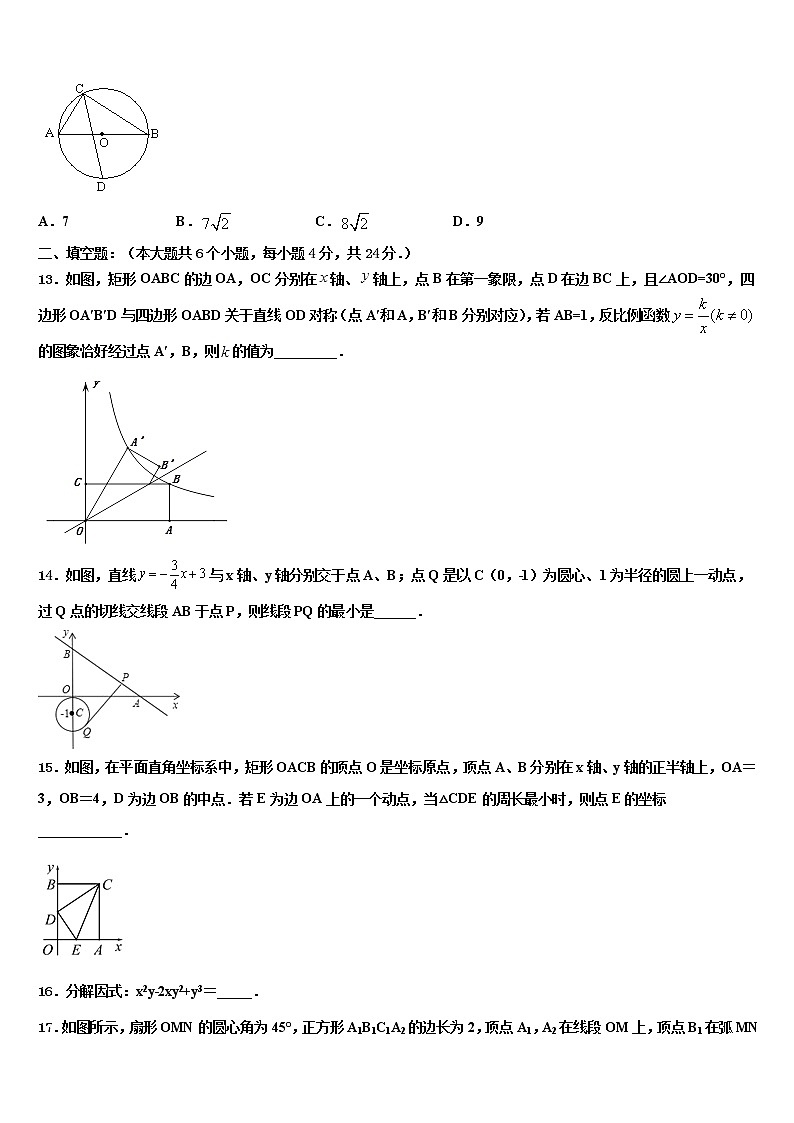
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．如图，矩形OABC的边OA，OC分别在轴、轴上，点B在第一象限，点D在边BC上，且∠AOD=30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，B′和B分别对应），若AB=1，反比例函数的图象恰好经过点A′，B，则的值为_________．
14．如图，直线与x轴、y轴分别交于点A、B；点Q是以C（0，﹣1）为圆心、1为半径的圆上一动点，过Q点的切线交线段AB于点P，则线段PQ的最小是______．
15．如图，在平面直角坐标系中，矩形OACB的顶点O是坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA＝3，OB＝4，D为边OB的中点．若E为边OA上的一个动点，当△CDE的周长最小时，则点E的坐标____________．
16．分解因式：x2y﹣2xy2+y3＝_____．
17．如图所示，扇形OMN的圆心角为45°，正方形A1B1C1A2的边长为2，顶点A1，A2在线段OM上，顶点B1在弧MN上，顶点C1在线段ON上，在边A2C1上取点B2，以A2B2为边长继续作正方形A2B2C2A3，使得点C2在线段ON上，点A3在线段OM上，……，依次规律，继续作正方形，则A2018M=__________．
18．如图，学校环保社成员想测量斜坡CD旁一棵树AB的高度，他们先在点C处测得树顶B的仰角为60°，然后在坡顶D测得树顶B的仰角为30°，已知DE⊥EA，斜坡CD的长度为30m，DE的长为15m，则树AB的高度是_____m．
三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）先化简，再求值：（1﹣）÷，其中x是不等式组的整数解
20．（6分）为了解朝阳社区岁居民最喜欢的支付方式，某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查（每人只能选择其中一项），并将调查数据整理后绘成如下两幅不完整的统计图．请根据图中信息解答下列问题：
求参与问卷调查的总人数．补全条形统计图．该社区中岁的居民约8000人，估算这些人中最喜欢微信支付方式的人数．
21．（6分）如图，在△ABC中，
（1）求作：∠BAD=∠C，AD交BC于D．（用尺规作图法，保留作图痕迹，不要求写作法）．
（2）在（1）条件下，求证：AB2=BD•BC．
22．（8分）如图，在Rt△ABC中，∠ACB＝90°，CD 是斜边AB上的高
（1）△ACD与△ABC相似吗？为什么？
（2）AC2＝AB•AD 成立吗？为什么？
23．（8分）某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y=﹣2x+1．设这种产品每天的销售利润为W元．
（1）该农户想要每天获得150元得销售利润，销售价应定为每千克多少元？
（2）如果物价部门规定这种农产品的销售价不高于每千克28元，销售价定为每千克多少元时，每天的销售利润最大？最大利润是多少元？
24．（10分）如图，已知∠ABC=90°，AB=BC．直线l与以BC为直径的圆O相切于点C．点F是圆O上异于B、C的动点，直线BF与l相交于点E，过点F作AF的垂线交直线BC于点D．
如果BE=15，CE=9，求EF的长；证明：①△CDF∽△BAF；②CD=CE；探求动点F在什么位置时，相应的点D位于线段BC的延长线上，且使BC=CD，请说明你的理由．
25．（10分）中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成，已知墙长为18米(如图所示)，设这个苗圃园垂直于墙的一边的长为x米.
(1)若苗圃园的面积为72平方米，求x；
(2)若平行于墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗?如果有，求出最大值和最小值；如果没有，请说明理由；
(3)当这个苗圃园的面积不小于100平方米时，直接写出x的取值范围.
26．（12分）我市某外资企业生产的一批产品上市后30天内全部售完，该企业对这批产品上市后每天的销售情况进行了跟踪调查．其中，国内市场的日销售量y1（万件）与时间t（t为整数，单位：天）的部分对应值如下表所示．而国外市场的日销售量y2（万件）与时间t（t为整数，单位：天）的关系如图所示．
（1）请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律，写出y1与t的函数关系式及自变量t的取值范围；
（2）分别探求该产品在国外市场上市20天前（不含第20天）与20天后（含第20天）的日销售量y2与时间t所符合的函数关系式，并写出相应自变量t的取值范围；
（3）设国内、外市场的日销售总量为y万件，写出y与时间t的函数关系式，并判断上市第几天国内、外市场的日销售总量y最大，并求出此时的最大值．
27．（12分）在平面直角坐标系中，O为原点，点A（8，0）、点B（0，4），点C、D分别是边OA、AB的中点．将△ACD绕点A顺时针方向旋转，得△AC′D′，记旋转角为α．
（I）如图①，连接BD′，当BD′∥OA时，求点D′的坐标；
（II）如图②，当α＝60°时，求点C′的坐标；
（III）当点B，D′，C′共线时，求点C′的坐标（直接写出结果即可）．
参考答案
一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、A
【解析】
分析：根据点A（a＋2，4）和B（3，2a＋2）到x轴的距离相等，得到4＝|2a＋2|，即可解答．
详解：∵点A（a＋2，4）和B（3，2a＋2）到x轴的距离相等，
∴4＝|2a＋2|，a＋2≠3，
解得：a＝−3，
故选A．
点睛：考查点的坐标的相关知识；用到的知识点为：到x轴和y轴的距离相等的点的横纵坐标相等或互为相反数．
2、C
【解析】
试题解析：原式=．
故选C.
考点：二次根式的乘除法．
3、B
【解析】
根据折叠前后对应角相等可知．
解：设∠ABE=x，
根据折叠前后角相等可知，∠C1BE=∠CBE=50°+x，
所以50°+x+x=90°，
解得x=20°．
故选B．
“点睛”本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
4、D
【解析】
【分析】先求AC,再根据点D是线段AC的中点，求出CD，再求BD.
【详解】因为，AB=10cm，BC=4cm，
所以，AC=AB-BC=10-4=6（cm）
因为，点D是线段AC的中点，
所以，CD=3cm,
所以，BD=BC+CD=3+4=7（cm）
故选D
【点睛】本题考核知识点：线段的中点，和差.解题关键点：利用线段的中点求出线段长度.
5、B
【解析】
根据抛物线的开口方向确定a，根据抛物线与y轴的交点确定c，根据对称轴确定b，根据抛物线与x轴的交点确定b2-4ac，根据x=1时，y＞0，确定a+b+c的符号．
【详解】
解：∵抛物线开口向上，
∴a＞0，
∵抛物线交于y轴的正半轴，
∴c＞0，
∴ac＞0，A错误；
∵-＞0，a＞0，
∴b＜0，∴B正确；
∵抛物线与x轴有两个交点，
∴b2-4ac＞0，C错误；
当x=1时，y＞0，
∴a+b+c＞0，D错误；
故选B．
【点睛】
本题考查的是二次函数图象与系数的关系，二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．
6、B
【解析】
根据“同大取大，同小取小，大小小大取中间，大大小小无解”即可求出字母a的取值范围.
【详解】
解：∵x的不等式组恰有3个整数解，
∴整数解为1，0，-1，
∴-2≤a＜-1.
故选B.
【点睛】
本题考查了一元一次不等式组的解法，先分别解两个不等式，求出它们的解集，再求两个不等式解集的公共部分.
7、D
【解析】
试题分析：根据中心对称图形的定义，结合选项所给图形进行判断即可．
解：A、不是中心对称图形，故本选项错误；
B、不是中心对称图形，故本选项错误；
C、不是中心对称图形，故本选项错误；
D、是中心对称图形，故本选项正确；
故选D．
考点：中心对称图形．
8、B
【解析】
根据第二象限中点的特征可得： ，
解得： .
在数轴上表示为：
故选B.
考点：(1)、不等式组；(2)、第一象限中点的特征
9、B
【解析】
∵抛物线C：y=x2+2x﹣3=（x+1）2﹣4，
∴抛物线对称轴为x=﹣1．
∴抛物线与y轴的交点为A（0，﹣3）．
则与A点以对称轴对称的点是B（2，﹣3）．
若将抛物线C平移到C′，并且C，C′关于直线x=1对称，就是要将B点平移后以对称轴x=1与A点对称．
则B点平移后坐标应为（4，﹣3），
因此将抛物线C向右平移4个单位．
故选B．
10、C
【解析】
如下图，设⊙O与射线AC相切于点D，连接OD，
∴∠ADO=90°，
∵∠BAC=45°，
∴△ADO是等腰直角三角形，
∴AD=DO=1，
∴OA=，此时⊙O与射线AC有唯一公共点点D，若⊙O再向右移动，则⊙O与射线AC就没有公共点了，
∴x的取值范围是.
故选C.
11、D
【解析】
试题分析：根据二次函数的图象依次分析各项即可。
由抛物线开口向上，可得，
再由对称轴是，可得，
由图象与y轴的交点再x轴下方，可得，
故选D.
考点：本题考查的是二次函数的性质
点评：解答本题的关键是熟练掌握二次函数的性质：的正负决定抛物线开口方向，对称轴是，C的正负决定与Y轴的交点位置。
12、B
【解析】
作DF⊥CA，交CA的延长线于点F，作DG⊥CB于点G，连接DA，DB．由CD平分∠ACB，根据角平分线的性质得出DF=DG，由HL证明△AFD≌△BGD，△CDF≌△CDG，得出CF=7，又△CDF是等腰直角三角形，从而求出CD=．
【详解】
解：作DF⊥CA，垂足F在CA的延长线上，作DG⊥CB于点G，连接DA，DB．
∵CD平分∠ACB，
∴∠ACD=∠BCD
∴DF=DG，弧AD=弧BD，
∴DA=DB．
∵∠AFD=∠BGD=90°，
∴△AFD≌△BGD，
∴AF=BG．
易证△CDF≌△CDG，
∴CF=CG．
∵AC=6，BC=8，
∴AF=1，（也可以：设AF=BG=x，BC=8，AC=6，得8-x=6+x，解x=1）
∴CF=7，
∵△CDF是等腰直角三角形，（这里由CFDG是正方形也可得）．
∴CD=．
故选B．
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、
【解析】
解：∵四边形ABCO是矩形，AB=1，
∴设B（m，1），
∴OA=BC=m，
∵四边形OA′B′D与四边形OABD关于直线OD对称，
∴OA′=OA=m，∠A′OD=∠AOD=30°，
∴∠A′OA=60°，
过A′作A′E⊥OA于E，
∴OE=m，A′E=m，
∴A′（m，m），
∵反比例函数y=（k≠0）的图象恰好经过点A′，B，
∴m•m=m，
∴m=，
∴k=．
【点睛】
本题考查反比例函数图象上点的坐标特征；矩形的性质，利用数形结合思想解题是关键．
14、
【解析】
解：过点C作CP⊥直线AB于点P，过点P作⊙C的切线PQ，切点为Q，此时PQ最小，连接CQ，如图所示．
当x=0时，y=3，∴点B的坐标为（0，3）；
当y=0时，x=4，∴点A的坐标为（4，0），∴OA=4，OB=3，∴AB==5，∴sinB=．
∵C（0，﹣1），∴BC=3﹣（﹣1）=4，∴CP=BC•sinB=．
∵PQ为⊙C的切线，∴在Rt△CQP中，CQ=1，∠CQP=90°，∴PQ==．
故答案为．
15、 (1，0)
【解析】
分析：由于C、D是定点，则CD是定值，如果的周长最小，即有最小值．为此，作点D关于x轴的对称点D′，当点E在线段CD′上时的周长最小．
详解：
如图,作点D关于x轴的对称点D′,连接CD′与x轴交于点E，连接DE.
若在边OA上任取点E′与点E不重合,连接CE′、DE′、D′E′
由DE′+CE′=D′E′+CE′>CD′=D′E+CE=DE+CE，
可知△CDE的周长最小，
∵在矩形OACB中，OA=3，OB=4，D为OB的中点，
∴BC=3,D′O=DO=2,D′B=6，
∵OE∥BC，
∴Rt△D′OE∽Rt△D′BC,有
∴OE=1，
∴点E的坐标为(1,0).
故答案为：(1,0).
点睛：考查轴对称-最短路线问题, 坐标与图形性质，相似三角形的判定与性质等,找出点E的位置是解题的关键.
16、y（x﹣y）2
【解析】
原式提取公因式，再利用完全平方公式分解即可
【详解】
x2y﹣2xy2+y3＝y（x2-2xy+y2）=y（x-y）2.
【点睛】
本题考查了提公因式法与公式法的综合运用，熟练掌握运算法则是解本题的关键．
17、．
【解析】
探究规律，利用规律即可解决问题.
【详解】
∵∠MON=45°，
∴△C2B2C2为等腰直角三角形，
∴C2B2=B2C2=A2B2．
∵正方形A2B2C2A2的边长为2，
∴OA3=AA3=A2B2=A2C2=2．OA2=4，OM=OB2=，
同理，可得出：OAn=An-2An=An-2An-2=，
∴OA2028=A2028A2027=，
∴A2028M=2-．
故答案为2-．
【点睛】
本题考查规律型问题，解题的关键是学会探究规律的方法，学会利用规律解决问题，属于中考常考题型．
18、1
【解析】
先根据CD=20米，DE=10m得出∠DCE=30°，故可得出∠DCB=90°，再由∠BDF=30°可知∠DBE=60°，由DF∥AE可得出∠BGF=∠BCA=60°，故∠GBF=30°，所以∠DBC=30°，再由锐角三角函数的定义即可得出结论．
【详解】
解：作DF⊥AB于F，交BC于G．则四边形DEAF是矩形，
∴DE=AF=15m，
∵DF∥AE，
∴∠BGF=∠BCA=60°，
∵∠BGF=∠GDB+∠GBD=60°，∠GDB=30°，
∴∠GDB=∠GBD=30°，
∴GD=GB，
在Rt△DCE中，∵CD=2DE，
∴∠DCE=30°，
∴∠DCB=90°，
∵∠DGC=∠BGF，∠DCG=∠BFG=90°
∴△DGC≌△BGF，
∴BF=DC=30m，
∴AB=30+15=1（m），
故答案为1．
【点睛】
本题考查的是解直角三角形的应用-仰角俯角问题，熟记锐角三角函数的定义是解答此题的关键．
三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、x=3时，原式=
【解析】
原式括号中两项通分并利用同分母分式的减法法则计算,再利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分得到最简结果,求出不等式组的解集,找出解集中的整数计算得出到x的值,代入计算即可求出值.
【详解】
解：原式=÷
=×
=，
解不等式组得，2＜x＜，
∵x取整数，
∴x=3，
当x=3时，原式=．
【点睛】
本题主要考查分式额化简求值及一元一次不等式组的整数解．
20、（1）参与问卷调查的总人数为500人；（2）补全条形统计图见解析；（3）这些人中最喜欢微信支付方式的人数约为2800人．
【解析】
（1）根据喜欢支付宝支付的人数÷其所占各种支付方式的比例=参与问卷调查的总人数，即可求出结论；
（2）根据喜欢现金支付的人数（41～60岁）=参与问卷调查的总人数×现金支付所占各种支付方式的比例-15，即可求出喜欢现金支付的人数（41～60岁），再将条形统计图补充完整即可得出结论；
（3）根据喜欢微信支付方式的人数=社区居民人数×微信支付所占各种支付方式的比例，即可求出结论．
【详解】
（1）（人．
答：参与问卷调查的总人数为500人．
（2）（人．
补全条形统计图，如图所示．
（3）（人．
答：这些人中最喜欢微信支付方式的人数约为2800人．
【点睛】
本题考查了条形统计图、扇形统计图以及用样本估计总体，解题的关键是：（1）观察统计图找出数据，再列式计算；（2）通过计算求出喜欢现金支付的人数（41～60岁）；（3）根据样本的比例×总人数，估算出喜欢微信支付方式的人数．
21、（1）作图见解析；（2）证明见解析；
【解析】
（1）①以C为圆心，任意长为半径画弧，交CB、CA于E、F；②以A为圆心，CE长为半径画弧，交AB于G；③以G为圆心，EF长为半径画弧，两弧交于H；④连接AH并延长交BC于D，则∠BAD=∠C；（2）证明△ABD∽△CBA，然后根据相似三角形的性质得到结论．
【详解】
（1）如图，∠BAD为所作；
（2）∵∠BAD=∠C，∠B=∠B
∴△ABD∽△CBA，
∴AB：BC=BD：AB，
∴AB2=BD•BC．
【点睛】
本题考查了基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线； 过一点作已知直线的垂线）．也考查了相似三角形的判定与性质．
22、（1）△ACD 与△ABC相似；（2）AC2＝AB•AD成立.
【解析】
（1）求出∠ADC＝∠ACB＝90°，根据相似三角形的判定推出即可；
（2）根据相似三角形的性质得出比例式，再进行变形即可．
【详解】
解：（1）△ACD 与△ABC相似，
理由是：∵在 Rt△ABC 中，∠ACB＝90°，CD 是斜边AB上的高，
∴∠ADC＝∠ACB＝90°，
∵∠A＝∠A，
∴△ACD∽∠ABC；
（2）AC2＝AB•AD成立，理由是：
∵△ACD∽∠ABC，
∴＝，
∴AC2＝AB•AD．
【点睛】
本题考查了相似三角形的性质和判定，能根据相似三角形的判定定理推出△ACD∽△ABC 是解此题的关键．
23、（1）该农户想要每天获得150元得销售利润，销售价应定为每千克25元或35元；（2）192元.
【解析】
（1）直接利用每件利润×销量=总利润进而得出等式求出答案；
（2）直接利用每件利润×销量=总利润进而得出函数关系式，利用二次函数增减性求出答案．
【详解】
（1）根据题意得：（x﹣20）（﹣2x+1）=150，
解得：x1=25，x2=35，
答：该农户想要每天获得150元得销售利润，销售价应定为每千克25元或35元；
（2）由题意得：W=（x﹣20）（﹣2x+1）=﹣2（x﹣30）2+200，
∵a=﹣2，
∴抛物线开口向下，当x＜30时，y随x的增大而增大，
又由于这种农产品的销售价不高于每千克28元
∴当x=28时，W最大=﹣2×（28﹣30）2+200=192（元）．
∴销售价定为每千克28元时，每天的销售利润最大，最大利润是192元.
【点睛】
此题主要考查了一元二次方程的应用以及二次函数的应用，正确应用二次函数增减性是解题关键．
24、（1） （2）证明见解析（3）F在直径BC下方的圆弧上，且
【解析】
（1）由直线l与以BC为直径的圆O相切于点C，即可得∠BCE=90°，∠BFC=∠CFE=90°，则可证得△CEF∽△BEC，然后根据相似三角形的对应边成比例，即可求得EF的长；
（2）①由∠FCD+∠FBC=90°，∠ABF+∠FBC=90°，根据同角的余角相等，即可得∠ABF=∠FCD，同理可得∠AFB=∠CFD，则可证得△CDF∽△BAF；
②由△CDF∽△BAF与△CEF∽△BCF，根据相似三角形的对应边成比例，易证得，又由AB=BC，即可证得CD=CE；
（3）由CE=CD，可得BC= CD=CE，然后在Rt△BCE中，求得tan∠CBE的值，即可求得∠CBE的度数，则可得F在⊙O的下半圆上，且.
【详解】
（1）解：∵直线l与以BC为直径的圆O相切于点C．
∴∠BCE=90°，
又∵BC为直径，
∴∠BFC=∠CFE=90°，
∵∠FEC=∠CEB，
∴△CEF∽△BEC，
∴，
∵BE=15，CE=9，
即：，
解得：EF= ；
（2）证明：①∵∠FCD+∠FBC=90°，∠ABF+∠FBC=90°，
∴∠ABF=∠FCD，
同理：∠AFB=∠CFD，
∴△CDF∽△BAF；
②∵△CDF∽△BAF，
∴，
又∵∠FCE=∠CBF，∠BFC=∠CFE=90°，
∴△CEF∽△BCF，
∴，
∴，
又∵AB=BC，
∴CE=CD；
（3）解：∵CE=CD，
∴BC=CD=CE，
在Rt△BCE中，tan∠CBE=，
∴∠CBE=30°，
故 为60°，
∴F在直径BC下方的圆弧上，且．
【点睛】
考查了相似三角形的判定与性质，圆的切线的性质，圆周角的性质以及三角函数的性质等知识．此题综合性很强，解题的关键是方程思想与数形结合思想的应用．
25、 (1) x=2；(2)苗圃园的面积最大为12.5平方米，最小为5平方米；(3) 6≤x≤4.
【解析】
（1）根据题意得方程求解即可；
（2）设苗圃园的面积为y，根据题意得到二次函数解析式y=x（31-2x）=-2x2+31x，根据二次函数的性质求解即可；
（3）由题意得不等式，即可得到结论.
【详解】
解：(1)苗圃园与墙平行的一边长为(31－2x)米．依题意可列方程
x(31－2x)＝72，即x2－15x＋36＝1．
解得x1＝3，x2＝2．
又∵31－2x≤3，即x≥6，
∴x=2
(2)依题意，得8≤31－2x≤3．解得6≤x≤4．
面积S＝x(31－2x)＝－2(x－)2＋(6≤x≤4)．
①当x＝时，S有最大值，S最大＝；
②当x＝4时，S有最小值，S最小＝4×(31－22)＝5．
(3)令x(31－2x)＝41，得x2－15x＋51＝1．
解得x1＝5，x2＝1
∴x的取值范围是5≤x≤4．
26、（1）y1=﹣t（t﹣30）（0≤t≤30）；（2）∴y2=；（3）上市第20天，国内、外市场的日销售总量y最大，最大值为80万件．
【解析】
(1)根据题意得出y1与t之间是二次函数关系，然后利用待定系数法求出函数解析式；
(2)利用待定系数法分别求出两个函数解析式，从而得出答案；
(3)分0≤t＜20、t=20和20≤t≤30三种情况根据y=y1+y2求出函数解析式，然后根据二次函数的性质得出最值，从而得出整体的最值．
【详解】
解：(1)由图表数据观察可知y1与t之间是二次函数关系，
设y1=a（t﹣0）（t﹣30）
再代入t=5，y1=25可得a=﹣
∴y1=﹣t（t﹣30）（0≤t≤30）
(2)由函数图象可知y2与t之间是分段的一次函数由图象可知：
0≤t＜20时，y2=2t，当20≤t≤30时，y2=﹣4t+120，
∴y2=，
(3)当0≤t＜20时，y=y1+y2=﹣t（t﹣30）+2t=80﹣（t﹣20）2 ，
可知抛物线开口向下，t的取值范围在对称轴左侧，y随t的增大而增大，所以最大值小于当t=20时的值80，
当20≤t≤30时，y=y1+y2=﹣t（t﹣30）﹣4t+120=125﹣（t﹣5）2 ，
可知抛物线开口向下，t的取值范围在对称轴右侧，y随t的增大而减小，所以最大值为当t=20时的值80，
故上市第20天，国内、外市场的日销售总量y最大，最大值为80万件．
27、（I）（10，4）或（6，4）（II）C′（6，2）（III）①C′（8，4）②
C′（，﹣）
【解析】
（I）如图①，当OB∥AC′，四边形OBC′A是平行四边形，只要证明B、C′、D′共线即可解决问题，再根据对称性确定D″的坐标；
（II）如图②，当α=60°时，作C′K⊥AC于K．解直角三角形求出OK，C′K即可解决问题；
（III）分两种情形分别求解即可解决问题；
【详解】
解:（I）如图①，
∵A（8，0），B（0，4），
∴OB=4，OA=8，
∵AC=OC=AC′=4，
∴当OB∥AC′，四边形OBC′A是平行四边形，
∵∠AOB=90°，
∴四边形OBC′A是矩形，
∴∠AC′B=90°，∵∠AC′D′=90°，
∴B、C′、D′共线，
∴BD′∥OA，
∵AC=CO， BD=AD，
∴CD=C′D′=OB=2，
∴D′（10，4），
根据对称性可知，点D″在线段BC′上时，D″（6，4）也满足条件．
综上所述，满足条件的点D坐标（10，4）或（6，4）．
（II）如图②，当α=60°时，作C′K⊥AC于K．
在Rt△AC′K中，∵∠KAC′=60°，AC′=4，
∴AK=2，C′K=2，
∴OK=6，
∴C′（6，2）．
（III）①如图③中，当B、C′、D′共线时，由（Ⅰ）可知，C′（8，4）．
②如图④中，当B、C′、D′共线时，BD′交OA于F，易证△BOF≌△AC′F，
∴OF=FC′，设OF=FC′=x，
在Rt△ABC′中，BC′==8，
在RT△BOF中，OB=4，OF=x，BF=8﹣x，
∴（8﹣x）2=42+x2，
解得x=3，
∴OF=FC′=3，BF=5，作C′K⊥OA于K，
∵OB∥KC′，
∴==，
∴==，
∴KC′=，KF=，
∴OK=，
∴C′（，﹣）．
【点睛】
本题考查三角形综合题、旋转变换、矩形的判定和性质、平行线的性质、勾股定理等知识，解题的关键是灵活应用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．