2021-2022学年湖南省怀化中学方县中考数学四模试卷含解析

这是一份2021-2022学年湖南省怀化中学方县中考数学四模试卷含解析，共25页。试卷主要包含了考生必须保证答题卡的整洁等内容，欢迎下载使用。
2021-2022中考数学模拟试卷
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．如图，△ABC纸片中，∠A＝56,∠C＝88°．沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD．则∠BDE的度数为（ ）

A．76° B．74° C．72° D．70°
2．如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，其顶点坐标为A（﹣1，﹣3），与x轴的一个交点为B（﹣3，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：①abc＞0；②不等式ax2+（b﹣m）x+c﹣n＜0的解集为﹣3＜x＜﹣1；③抛物线与x轴的另一个交点是（3，0）；④方程ax2+bx+c+3=0有两个相等的实数根；其中正确的是（　　）

A．①③ B．②③ C．③④ D．②④
3．如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为（ ）

A．1 B．2 C．3 D．4
4．如图是由5个大小相同的正方体组成的几何体，则该几何体的左视图是（　　）

A． B．
C． D．
5．如图，AB∥CD，FE⊥DB，垂足为E，∠1=60°，则∠2的度数是（　　）

A．60° B．50° C．40° D．30°
6．甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟，在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t（分）之间的关系如图所示，下列结论：
①甲步行的速度为60米/分；
②乙走完全程用了32分钟；
③乙用16分钟追上甲；
④乙到达终点时，甲离终点还有300米
其中正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个
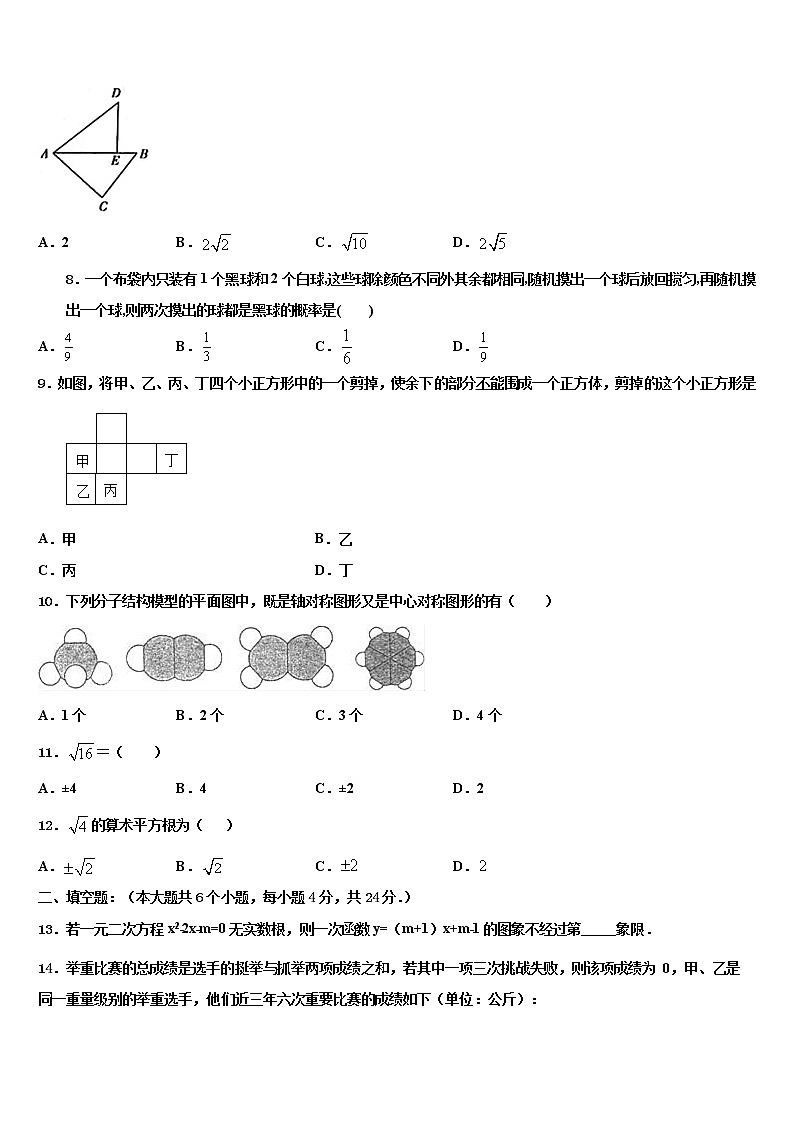
7．如图所示，在△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则BD两点间的距离为（ ）

A．2 B． C． D．
8．一个布袋内只装有1个黑球和2个白球,这些球除颜色不同外其余都相同,随机摸出一个球后放回搅匀,再随机摸出一个球,则两次摸出的球都是黑球的概率是( )
A． B． C． D．
9．如图，将甲、乙、丙、丁四个小正方形中的一个剪掉，使余下的部分不能围成一个正方体，剪掉的这个小正方形是

A．甲 B．乙
C．丙 D．丁
10．下列分子结构模型的平面图中，既是轴对称图形又是中心对称图形的有（　　）

A．1个 B．2个 C．3个 D．4个
11．＝（　　）
A．±4 B．4 C．±2 D．2
12．的算术平方根为（ ）
A． B． C． D．
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．若一元二次方程x2﹣2x﹣m=0无实数根，则一次函数y=（m+1）x+m﹣1的图象不经过第_____象限．
14．举重比赛的总成绩是选手的挺举与抓举两项成绩之和，若其中一项三次挑战失败，则该项成绩为 0，甲、乙是同一重量级别的举重选手，他们近三年六次重要比赛的成绩如下（单位：公斤）：

如果你是教练，要选派一名选手参加国际比赛，那么你会选择_____（填“甲” 或“乙”），理由是___________．
15．如图△ABC中，AB=AC=8，∠BAC=30°，现将△ABC绕点A逆时针旋转30°得到△ACD，延长AD、BC交于点E，则DE的长是_____．

16．分式有意义时，x的取值范围是_____．
17．某商场将一款品牌时装按标价打九折出售，可获利80%，这款商品的标价为1000元，则进价为 ________元。
18．若圆锥的地面半径为，侧面积为，则圆锥的母线是__________．
三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）凯里市某文具店某种型号的计算器每只进价12元，售价20元，多买优惠，优势方法是：凡是一次买10只以上的，每多买一只，所买的全部计算器每只就降价0.1元，例如：某人买18只计算器，于是每只降价0.1×（18﹣10）=0.8（元），因此所买的18只计算器都按每只19.2元的价格购买，但是每只计算器的最低售价为16元．求一次至少购买多少只计算器，才能以最低价购买？求写出该文具店一次销售x（x＞10）只时，所获利润y（元）与x（只）之间的函数关系式，并写出自变量x的取值范围；一天，甲顾客购买了46只，乙顾客购买了50只，店主发现卖46只赚的钱反而比卖50只赚的钱多，请你说明发生这一现象的原因；当10＜x≤50时，为了获得最大利润，店家一次应卖多少只？这时的售价是多少？
20．（6分）如图，在梯形中，,,,,点为边上一动点，作⊥,垂足在边上，以点为圆心，为半径画圆，交射线于点.
（1）当圆过点时，求圆的半径；
（2）分别联结和，当时，以点为圆心，为半径的圆与圆相交，试求圆的半径的取值范围；
（3）将劣弧沿直线翻折交于点,试通过计算说明线段和的比值为定值，并求出次定值.

21．（6分）吴京同学根据学习函数的经验，对一个新函数y＝的图象和性质进行了如下探究，请帮他把探究过程补充完整该函数的自变量x的取值范围是　 　．列表：
x
…
﹣2
﹣1
0
1
2
3
4
5
6
…
y
…

m
﹣1

﹣5
n
﹣1


…
表中m＝　 　，n＝　 　．描点、连线
在下面的格点图中，建立适当的平面直角坐标系xOy中，描出上表中各对对应值为坐标的点（其中x为横坐标，y为纵坐标），并根据描出的点画出该函数的图象：
观察所画出的函数图象，写出该函数的两条性质：
①　 　；
②　 　．
22．（8分）为响应“学雷锋、树新风、做文明中学生”号召，某校开展了志愿者服务活动，活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项，活动期间，随机抽取了部分学生对志愿者服务情况进行调查，结果发现，被调查的每名学生都参与了活动，最少的参与了1项，最多的参与了5项，根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图．
被随机抽取的学生共有多少名？在扇形统计图中，求活动数为3项的学生所对应的扇形圆心角的度数，并补全折线统计图；该校共有学生2000人，估计其中参与了4项或5项活动的学生共有多少人？
23．（8分）某校诗词知识竞赛培训活动中，在相同条件下对甲、乙两名学生进行了10次测验，他们的10次成绩如下（单位：分）：整理、分析过程如下，请补充完整．

（1）按如下分数段整理、描述这两组数据：
成绩x
学生
70≤x≤74
75≤x≤79
80≤x≤84
85≤x≤89
90≤x≤94
95≤x≤100
甲
______
______
______
______
______
______
乙
1
1
4
2
1
1
（2）两组数据的极差、平均数、中位数、众数、方差如下表所示：
学生
极差
平均数
中位数
众数
方差
甲
______
83.7
______
86
13.21
乙
24
83.7
82
______
46.21
（3）若从甲、乙两人中选择一人参加知识竞赛，你会选______（填“甲”或“乙），理由为______．
24．（10分）如图所示，平行四边形形ABCD中，过对角线BD中点O的直线分别交AB，CD边于点E，F．
（1）求证：四边形BEDF是平行四边形；
（2）请添加一个条件使四边形BEDF为菱形．

25．（10分）某农场用2台大收割机和5台小收割机同时工作2小时共收割小麦3.6公顷，3台大收割机和2台小收割机同时工作5小时共收割小麦8公顷.1台大收割机和1台小收割机每小时各收割小麦多少公顷？
26．（12分）如图，在矩形ABCD中，AD＝4，点E在边AD上，连接CE，以CE为边向右上方作正方形CEFG，作FH⊥AD，垂足为H，连接AF.
(1)求证：FH＝ED；
(2)当AE为何值时，△AEF的面积最大？

27．（12分）如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=1OD，OE=1OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．

（1）求证：DE⊥AG；
（1）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°）得到正方形OE′F′G′，如图1．
①在旋转过程中，当∠OAG′是直角时，求α的度数；
②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．



参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、B
【解析】
直接利用三角形内角和定理得出∠ABC的度数，再利用翻折变换的性质得出∠BDE的度数．
【详解】
解：∵∠A=56°，∠C=88°，
∴∠ABC=180°-56°-88°=36°，
∵沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，
∴∠CBD=∠DBE=18°，∠C=∠DEB=88°，
∴∠BDE=180°-18°-88°=74°．
故选：B．
【点睛】
此题主要考查了三角形内角和定理，正确掌握三角形内角和定理是解题关键．
2、D
【解析】
①错误．由题意a＞1．b＞1，c＜1，abc＜1；
②正确．因为y1=ax2+bx+c（a≠1）图象与直线y2=mx+n（m≠1）交于A，B两点，当ax2+bx+c＜mx+n时，-3＜x＜-1；即不等式ax2+（b-m）x+c-n＜1的解集为-3＜x＜-1；故②正确；
③错误．抛物线与x轴的另一个交点是（1，1）；
④正确．抛物线y1=ax2+bx+c（a≠1）图象与直线y=-3只有一个交点，方程ax2+bx+c+3=1有两个相等的实数根，故④正确．
【详解】
解：∵抛物线开口向上，∴a＞1，
∵抛物线交y轴于负半轴，∴c＜1，
∵对称轴在y轴左边，∴- ＜1，
∴b＞1，
∴abc＜1，故①错误．
∵y1=ax2+bx+c（a≠1）图象与直线y2=mx+n（m≠1）交于A，B两点，
当ax2+bx+c＜mx+n时，-3＜x＜-1；
即不等式ax2+（b-m）x+c-n＜1的解集为-3＜x＜-1；故②正确，
抛物线与x轴的另一个交点是（1，1），故③错误，
∵抛物线y1=ax2+bx+c（a≠1）图象与直线y=-3只有一个交点，
∴方程ax2+bx+c+3=1有两个相等的实数根，故④正确．
故选：D．
【点睛】
本题考查二次函数的性质、二次函数与不等式，二次函数与一元二次方程等知识，解题的关键是灵活运用所学知识解决问题，学会利用数形结合的思想解决问题．
3、C
【解析】
∵∠ACD=∠B，∠A=∠A，
∴△ACD∽△ABC，
∴，
∴，
∴，
∴S△ABC=4，
∴S△BCD= S△ABC- S△ACD=4-1=1．
故选C
考点：相似三角形的判定与性质.
4、B
【解析】
找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．
【详解】
解：从左面看易得下面一层有2个正方形，上面一层左边有1个正方形．
故选：B．
【点睛】
本题考查了三视图的知识，左视图是从物体的左面看得到的视图．
5、D
【解析】
由EF⊥BD，∠1=60°，结合三角形内角和为180°即可求出∠D的度数，再由“两直线平行，同位角相等”即可得出结论．
【详解】
解：在△DEF中，∠1=60°，∠DEF=90°，
∴∠D=180°-∠DEF-∠1=30°．
∵AB∥CD，
∴∠2=∠D=30°．
故选D．
【点睛】
本题考查平行线的性质以及三角形内角和为180°,解题关键是根据平行线的性质，找出相等、互余或互补的角．
6、A
【解析】
【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否正确，从而可以解答本题．
【详解】由图可得，
甲步行的速度为：240÷4=60米/分，故①正确，
乙走完全程用的时间为：2400÷（16×60÷12）=30（分钟），故②错误，
乙追上甲用的时间为：16﹣4=12（分钟），故③错误，
乙到达终点时，甲离终点距离是：2400﹣（4+30）×60=360米，故④错误，
故选A．
【点睛】本题考查了函数图象，弄清题意，读懂图象，从中找到必要的信息是解题的关键.
7、C
【解析】
解：连接BD．在△ABC中，∵∠C=90°，AC=4，BC=3，∴AB=2．∵将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，∴AE=4，DE=3，∴BE=2．在Rt△BED中，BD=．故选C．

点睛：本题考查了勾股定理和旋转的基本性质，解决此类问题的关键是掌握旋转的基本性质，特别是线段之间的关系．题目整体较为简单，适合随堂训练．
8、D
【解析】
试题分析：列表如下


黑

白1

白2

黑

（黑，黑）

（白1，黑）

（白2，黑）

白1

（黑，白1）

（白1，白1）

（白2，白1）

白2

（黑，白2）

（白1，白2）

（白2，白2）

由表格可知，随机摸出一个球后放回搅匀，再随机摸出一个球所以的结果有9种，两次摸出的球都是黑球的结果有1种，所以两次摸出的球都是黑球的概率是．故答案选D．
考点：用列表法求概率．
9、D
【解析】
解：将如图所示的图形剪去一个小正方形，使余下的部分不能围成一个正方体，编号为甲乙丙丁的小正方形中剪去的是丁．故选D．
10、C
【解析】
根据轴对称图形与中心对称图形的概念求解．
【详解】
解：A是轴对称图形，不是中心对称图形；B，C，D是轴对称图形，也是中心对称图形．
故选:C．
【点睛】
掌握中心对称图形与轴对称图形的概念：轴对称图形：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形；中心对称图形：在同一平面内，如果把一个图形绕某一点旋转180°，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形．
11、B
【解析】
表示16的算术平方根，为正数，再根据二次根式的性质化简．
【详解】
解：，
故选B．
【点睛】
本题考查了算术平方根，本题难点是平方根与算术平方根的区别与联系，一个正数算术平方根有一个，而平方根有两个．
12、B
【解析】
分析：先求得的值，再继续求所求数的算术平方根即可．
详解：∵=2，
而2的算术平方根是，
∴的算术平方根是，
故选B．
点睛：此题主要考查了算术平方根的定义，解题时应先明确是求哪个数的算术平方根，否则容易出现选A的错误．

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、一
【解析】
∵一元二次方程x2-2x-m=0无实数根，
∴△=4+4m＜0，解得m＜-1，
∴m+1＜0，m-1＜0，
∴一次函数y=（m+1）x+m-1的图象经过二三四象限，不经过第一象限．
故答案是：一．
14、乙 乙的比赛成绩比较稳定．
【解析】
观察表格中的数据可知：甲的比赛成绩波动幅度较大，故甲的比赛成绩不稳定；乙的比赛成绩波动幅度较小，故乙的比赛成绩比较稳定，据此可得结论．
【详解】
观察表格中的数据可得，甲的比赛成绩波动幅度较大，故甲的比赛成绩不稳定； 乙的比赛成绩波动幅度较小，故乙的比赛成绩比较稳定；
所以要选派一名选手参加国际比赛，应该选择乙，理由是乙的比赛成绩比较稳定．
故答案为乙，乙的比赛成绩比较稳定．
【点睛】
本题主要考查了方差，方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
15、
【解析】
过点作于，根据三角形的性质及三角形内角和定理可计算
再由旋转可得，，根据三角形外角和性质计算，根据含角的直角三角形的三边关系得和的长度，进而得到的长度，然后利用得到与的长度，于是可得.
【详解】
如图，过点作于，
∵，
∴．
∵将绕点逆时针旋转，使点落在点处，此时点落在点处，
∴
∵
∴
在中，∵
∴
∴，
在中，∵，
∴，
∴．
故答案为．
【点睛】
本题考查三角形性质的综合应用，要熟练掌握等腰三角形的性质，含角的直角三角形的三边关系，旋转图形的性质．
16、x＜1
【解析】
要使代数式有意义时，必有1﹣x＞2，可解得x的范围．
【详解】
根据题意得：1﹣x＞2，
解得：x＜1．
故答案为x＜1．
【点睛】
考查了分式和二次根式有意义的条件．二次根式有意义，被开方数为非负数，分式有意义，分母不为2．
17、500
【解析】
设该品牌时装的进价为x元，根据题意列出方程，求出方程的解得到x的值，即可得到结果.
【详解】
解：设该品牌时装的进价为x元，根据题意得：1000×90%-x=80%x，解得：x=500，则该品牌时装的进价为500元.
故答案为：500.
【点睛】
本题考查了一元一次方程的应用，找出题中的等量关系是解本题的关键.
18、13
【解析】
试题解析：圆锥的侧面积=×底面半径×母线长，把相应数值代入即可求解．
设母线长为R，则：
解得:
故答案为13.

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、（1）1；（3）；（3）理由见解析，店家一次应卖45只，最低售价为16.5元，此时利润最大．
【解析】
试题分析：（1）设一次购买x只，由于凡是一次买10只以上的，每多买一只，所买的全部计算器每只就降低0.10元，而最低价为每只16元，因此得到30﹣0.1（x﹣10）=16，解方程即可求解；
（3）由于根据（1）得到x≤1，又一次销售x（x＞10）只，因此得到自变量x的取值范围，然后根据已知条件可以得到y与x的函数关系式；
（3）首先把函数变为y==，然后可以得到函数的增减性，再结合已知条件即可解决问题．
试题解析：（1）设一次购买x只，则30﹣0.1（x﹣10）=16，解得：x=1．
答：一次至少买1只，才能以最低价购买；
（3）当10＜x≤1时，y=[30﹣0.1（x﹣10）﹣13]x=，当x＞1时，y=（16﹣13）x=4x；
综上所述：；
（3）y==，①当10＜x≤45时，y随x的增大而增大，即当卖的只数越多时，利润更大．
②当45＜x≤1时，y随x的增大而减小，即当卖的只数越多时，利润变小．
且当x=46时，y1=303.4，当x=1时，y3=3．∴y1＞y3．
即出现了卖46只赚的钱比卖1只赚的钱多的现象．
当x=45时，最低售价为30﹣0.1（45﹣10）=16.5（元），此时利润最大．故店家一次应卖45只，最低售价为16.5元，此时利润最大．
考点：二次函数的应用；二次函数的最值；最值问题；分段函数；分类讨论．
20、（1）x=1 （2） （1）
【解析】
(1)作AM⊥BC、连接AP，由等腰梯形性质知BM=4、AM=1，据此知tanB=tanC= ，从而可设PH=1k，则CH=4k、PC=5k，再表示出PA的长，根据PA=PH建立关于k的方程，解之可得；
(2)由PH=PE=1k、CH=4k、PC=5k及BC=9知BE=9−8k，由△ABE∽△CEH得 ，据此求得k的值，从而得出圆P的半径，再根据两圆间的位置关系求解可得；
(1)在圆P上取点F关于EH的对称点G，连接EG，作PQ⊥EG、HN⊥BC，先证△EPQ≌△PHN得EQ=PN，由PH=1k、HC=4k、PC=5k知sinC= 、cosC= ，据此得出NC= k、HN=k及PN=PC−NC=k，继而表示出EF、EH的长，从而出答案．
【详解】
(1)作AM⊥BC于点M，连接AP，如图1，

∵梯形ABCD中，AD//BC，且AB=DC=5、AD=1、BC=9，
∴BM=4、AM=1，
∴tanB=tanC=，
∵PH⊥DC，
∴设PH=1k，则CH=4k、PC=5k，
∵BC=9，
∴PM=BC−BM−PC=5−5k，
∴AP=AM+PM=9+(5−5k) ，
∵PA=PH，
∴9+(5−5k) =9k，
解得：k=1或k=，
当k= 时，CP=5k= >9，舍去；
∴k=1，
则圆P的半径为1．
(2)如图2，

由(1)知，PH=PE=1k、CH=4k、PC=5k，
∵BC=9，
∴BE=BC−PE−PC=9−8k，
∵△ABE∽△CEH，
∴ ，即 ，
解得：k= ，
则PH= ，即圆P的半径为，
∵圆B与圆P相交，且BE=9−8k= ，
∴