2021学年3 三角形的中位线课堂教学课件ppt

这是一份2021学年3 三角形的中位线课堂教学课件ppt，共15页。

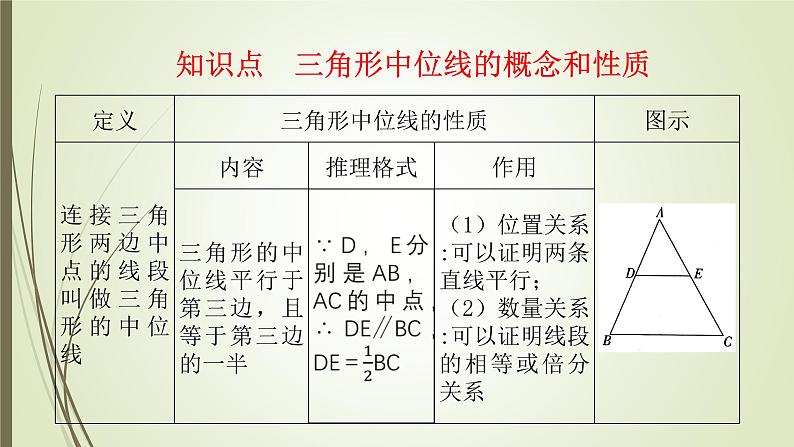
知识点 三角形中位线的概念和性质
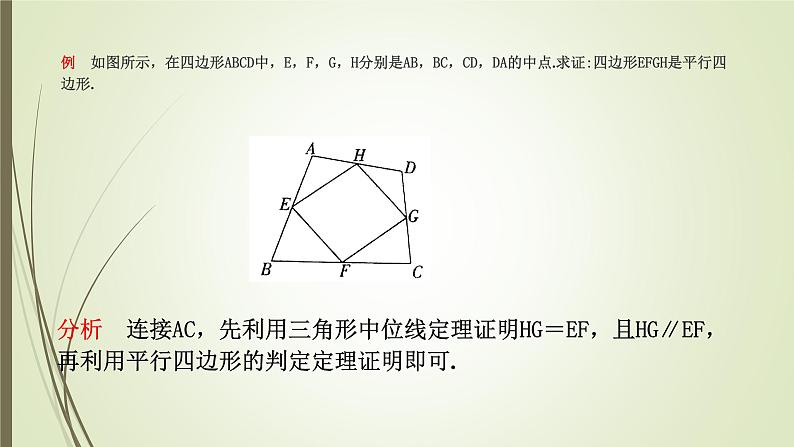
例 如图所示，在四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点.求证:四边形EFGH是平行四边形.
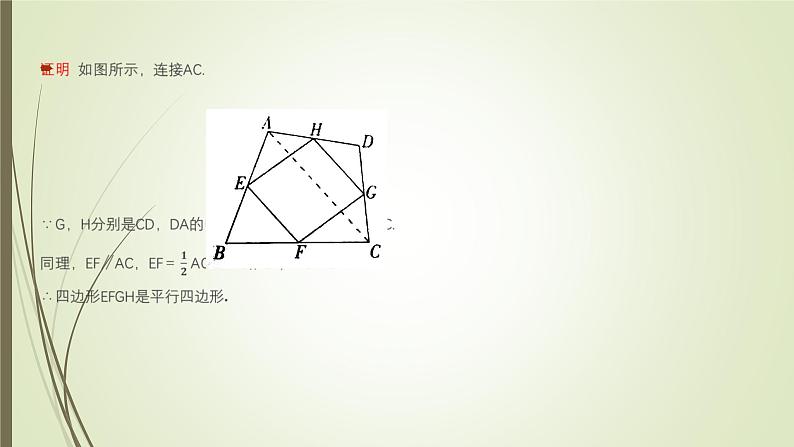
分析 连接AC，先利用三角形中位线定理证明HG＝EF，且HG∥EF，再利用平行四边形的判定定理证明即可.
方法归纳 当题目中出现线段的中点时，一般连接中点，考虑用三角形的中位线定理来解决，本题还可以再连接BD，利用两组对边分别平行的四边形是平行四边形来解决.
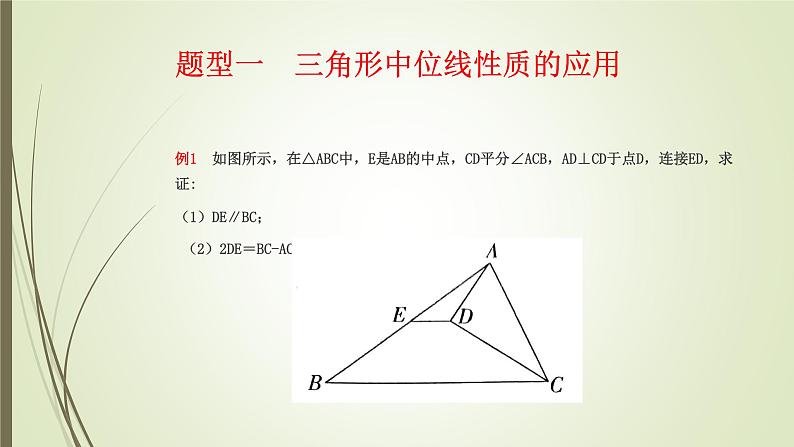
题型一 三角形中位线性质的应用
例1 如图所示，在△ABC中，E是AB的中点，CD平分∠ACB，AD⊥CD于点D，连接ED，求证:（1）DE∥BC； （2）2DE＝BC-AC.
分析 （1）延长AD交BC于点F，根据△ACD≌△FCD得到AC＝CF，AD＝DF，故可得出DE∥BC.（2）根据AC＝CF可得出BF＝BC-CF＝BC-AC，由三角形中位线定理即可得出结论.
点拨 当问题中有中点，且证明线段平行或2倍关系时，我们通常考虑问题能不能应用三角形中位线定理解决.
题型二 构造三角形的中位线解题
例2 如图所示，在四边形ABCD中，对角线AC、BD相交于点O，且AC＝BD，E、F分别是AB、CD的中点，EF分别交BD、AC于点G、H.求证:OG＝OH.
分析 取BC边的中点M，连接EM，FM，首先根据三角形的中位线定理得到△EMF是等腰三角形，然后根据等边对等角得到∠MEF＝∠MFE，再根据平行线的性质得到∠OGH＝∠OHG，最后根据等角对等边即可证得结论.
点拨 已知三角形一边的中点时，常作辅助线构造出三角形的中位线.