湖南省怀化市新晃县2021-2022学年八年级下学期期末质量检测数学试题（乡镇）（含答案）

新晃县2022年上期乡镇中学期末质量检测试卷

八年级数学

考生注意：1.本试卷三道大题。考试时间120分钟，满分150分。

2.本试卷分答题卷和答题卡，请在答题卡上作答。

一、选择题（每小题4分，共40分，每个小题都给出四个选项，只有唯一一个是正确的，请选出正确的选项）

1、点（，3）所在的位置是（）

A．第一象限     B．第二象限   C．第三象限  D．第四象限

2、下列四组数据不能作为直角三角形的三边长的是（）

A．3，4，5      B．，， C．6，8，10     D．2，4，6

3、一个边形的内角和是720°，则等于（）

A．4  B．5   C．6   D．7

4、下列函数中，正比例函数是（）

A.   B.  C.  D. .

5、在下列图形中，既是中心对称图形，又是轴对称图形的是（）

A．B． C． D．

6、如图，在平行四边形ABCD中，∠ABC的角平分线交边AD于点E，∠C＝130°，则∠AEB的度数是（）

A．20°    B．25°    C．30°    D．35°

7、一次函数的图象如图，则下列说法正确的是（）

A．                 B．

C．随的增大而增大    D．时，

8、“早发现，早报告，早隔离，早治疗”是我国抗击“新冠肺炎”的宝贵经验，这个经验中“早”字出现的频率是（　　）

A． B． C． D．

9、一个三角形的周长是36cm，则以这个三角形各边中点为顶点的三角形的周长是（）

A. 6cm B. 12cm C. 18cm D. 36cm

10、在四边形ABCD中，AB＝DC，AD＝BC.请再添加一个条件，使四边形ABCD是矩形．添加的条件不能是（）

A. AC⊥BD B. ∠A＝90° C. ∠C＝∠D        D. AC＝BD

二、填空题（每小题4分，共24分）

11、点 P（3，）关于轴的对称点坐标是.

12、一次函数的图象不经过第象限.

13、在Rt△ABC中，∠C=90°，∠A=60°，AB=10，则AC=.

14、八年级甲班的50位同学中，1月份出生的频率是0.3，这个班1月份出生的同学有人.

15、如图，在菱形ABCD中，若AC=12，BD=16，则菱形ABCD边长是________．

16、甲、乙两人在一次跨栏比赛中，路程s（m）与时间t（s）的函数关系如图所示，根据图形，下列说法：

①这次比赛的赛程是110米；

②甲先到达终点；

③乙在这次比赛中的平均速度为m/s；

④乙的平均速度比甲快。

其中正确的是（填序号）.

三、解答题（共86分）

17、（8分）已知点M(，)是轴上的点.

（1）求的值.

（2）若将点M向左平移2个单位得到点N，写出N点的坐标.

18、（8分）已知正比例函数的图象经过点A（，5）.

（1）求这个函数表达式。

（2）点B（2，10）、C（，15）是否在这个函数的图象上？

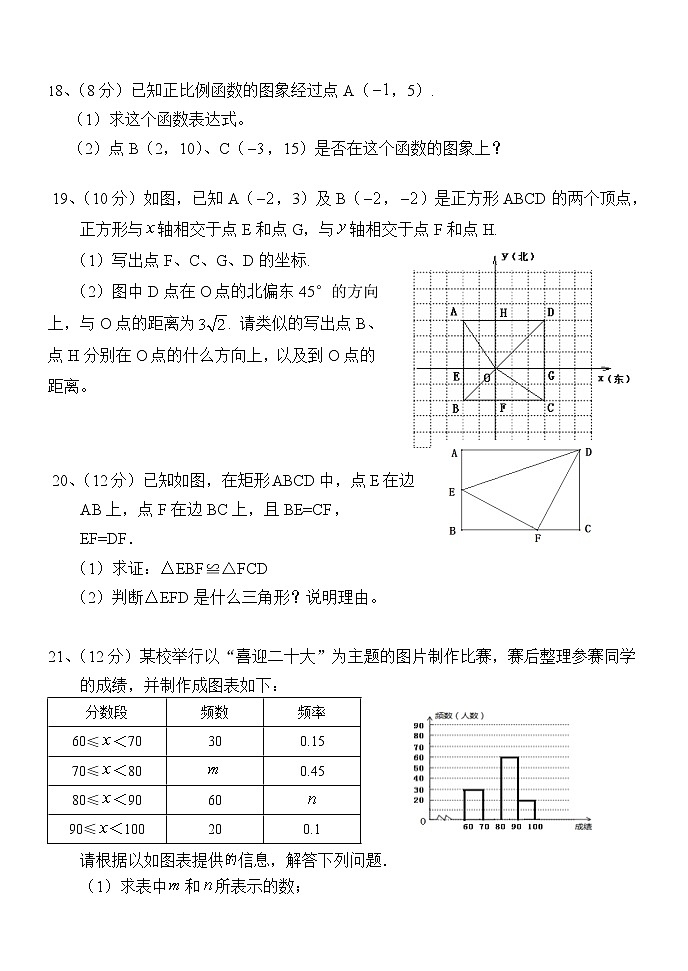
19、（10分）如图，已知A（，3）及B（，）是正方形ABCD的两个顶点，正方形与轴相交于点E和点G，与轴相交于点F和点H.

   （1）写出点F、C、G、D的坐标.

（2）图中D点在O点的北偏东45°的方向上，与O点的距离为. 请类似的写出点B、点H分别在O点的什么方向上，以及到O点的距离。

20、（12分）已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF， EF=DF．

（1）求证：△EBF≌△FCD

（2）判断△EFD是什么三角形？说明理由。
 

21、（12分）某校举行以“喜迎二十大”为主题的图片制作比赛，赛后整理参赛同学的成绩，并制作成图表如下：

请根据以如图表提供信息，解答下列问题．

（1）求表中和所表示的数；

（2）请在图中补全频数分布直方图；

（3）若比赛成绩不低于80分可以获奖，则获奖率为多少？

22、（12分）如图，已知一次函数的图象经过点A（，）和B（4，4），与轴交于点C，与轴交于点D．

（1）求一次函数的表达式；

（2）求C、D点的坐标，并根据函数图象，直接写出当＜＜0时，的取值范围．

23、（12分）如图，在矩形ABCD中，过对角线AC的中点O作垂线EF交边BC，AD分别为点E，F，连接AE，CF.

(1)求证：四边形AECF是菱形；

(2)若AD＝8，AB＝4，求CF长．

24、（12分）由于疫情的影响，“摆地摊”成为了很多人经济来源的一种形式．某摊主从市场得知如下信息：

该摊主计划购进A．B商品共100件进行销售，设购进A商品件，A．B商品全部销售完后获得利润为元．

（1）求出与之间的函数关系式；

（2）若该摊主用不超过2000元资金一次性购进A．B两种商品，则如何进货，才能使得获利最大？并求出最大利润．

新晃县2022年上期乡镇中学期末质量检测试卷

八年级数学参考答案及评分标准

一、选择题  BDCDC BBDCA

二、填空题11、（-3，-4）；12、二；13、.5；14、15；15、10；16、①②③

三、解答题

17、（1）2020；（4分）（2）（-2，-4）（4分）

18、（1）；（4分）（2） B不在，C在（4分）

19、（1）F（0，-2）、C（3，-2）、G（3，0）、D（3，3）；（4分）

（2）点B在O点的西偏南45°的方向上，与O点的距离为；点H在O点的正北方向上，与O点的距离为3.（6分）

20、（1）证明：四边形ABCD是矩形，∴（2分）

在Rt△EBF和Rt△FCD中
 

∴Rt△EBF≌Rt△FCD（HL）（6分）

（2）△EFD是等腰直角三角形（2分），说理正确（4分）

21、（1）=90，= 0.3（4分）；（2）画图正确（4分）；（3）40%.（4分）

22、（1）设一次函数的解析式为，（1分）得

  （3分）解之得  （5分）

 ∴一次函数的表达式为（6分）

（2）时，∴D点为（0，-2），（2）分）时，，∴C点为（，0）（4分）.当﹣5＜＜0时，的取值范围是．（6分）

23（1）证明：∵四边形ABCD是矩形，∴AD∥BC，∠AFO＝∠CEO.

∵点O为AC的中点，∴AO＝OC.

在△AFO和△CEO中，

,

∴△AFO≌△CEO(AAS)，∴OE＝OF，

∴四边形AECF是平行四边形．

∵EF⊥AC，

∴平行四边形AECF是菱形．（6分）

（2）解：∵四边形ABCD是矩形，∴∠B＝90°.

由(1)知四边形AECF是菱形，

∴设AE＝CE＝CF＝x.则BE＝8－x.

在Rt△ABE中，，即，解得x＝5，

∴CF＝5.（6分）

24、（1）解：（6分）

（2）解：由题意可得：35x+5（100﹣x）≤2000，解得：x≤50，

又∵x≥0，∴0≤x≤50，

∵y＝7x+300，7＞0，

∴y随x的增大而增大，

∴当x＝50时，可获得最大利润，最大利润为：y＝7×50+300＝650（元），

100﹣x＝100﹣50＝50（件）．

所当购进A种商品50件，B种商品50件时，可使得A、B商品全部销售完后获得的利润最大，最大利润650元．（6分）