2021济南高三下学期5月高考模拟针对训练（三模）数学含答案

www.ks5u.com绝密★启用并使用完毕前

2021年5月高考针对性训练

数学试题

本试卷共4页，22题，全卷满分150分。考试用时120分钟。

注意事项：

1.答卷前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知复数z＝(其中i为虚数单位)，则z在复平面内所对应的点在

A.第一象限       B.第二象限      C.第三象限     D.第四象限

2.(x＋)6的展开式中，含x4项的系数为

A.4     B.6     C.10     D.15

3.△ABC中，“sinA＝”是“A＝”的

A.充要条件    B.充分不必要条件    C.必要不充分条件    D.既不充分也不必要条件

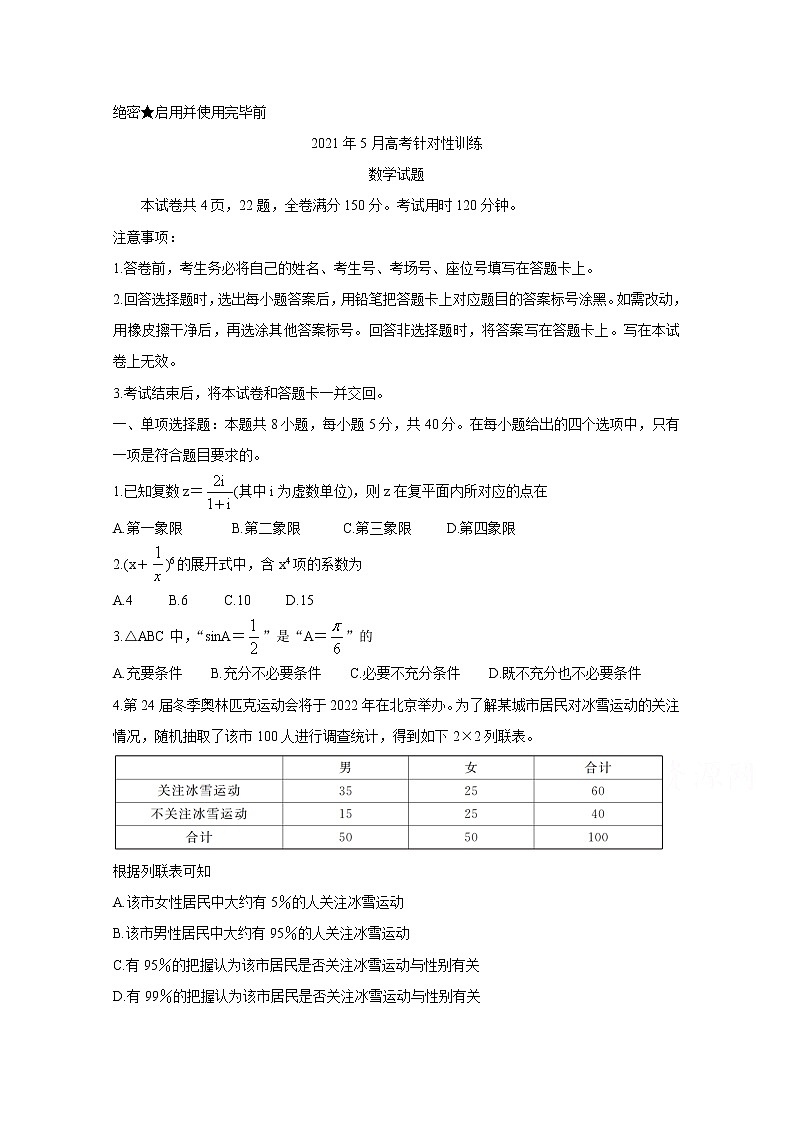
4.第24届冬季奥林匹克运动会将于2022年在北京举办。为了解某城市居民对冰雪运动的关注情况，随机抽取了该市100人进行调查统计，得到如下2×2列联表。

根据列联表可知

A.该市女性居民中大约有5％的人关注冰雪运动

B.该市男性居民中大约有95％的人关注冰雪运动

C.有95％的把握认为该市居民是否关注冰雪运动与性别有关

D.有99％的把握认为该市居民是否关注冰雪运动与性别有关

参考公式：，其中n＝a＋b＋c＋d。

附表：

5.将函数f(x)＝sinx＋cosx的图象向右平移个单位后，得到函数g(x)的图象，则下列关于g(x)的说法正确的是

A.最小正周期为π                     B.最小值为－1

C.图象关于点(，0)中心对称         D.图象关于直线x＝对称

6.已知抛物线x2＝2py(p>0)，过焦点F的直线与抛物线交于A，B两点(点A在第一象限)。若直线AB的斜率为，点A的纵坐标为，则p的值为

A.     B.12     C.1     D.2

7.苏格兰数学家纳皮尔发明了对数表，这一发明为当时天文学家处理“大数运算”提供了巨大的便利。已知正整数N的31次方是一个35位数，则由下面的对数表，可得N的值为

A.12     B.13     C.14     D.15

8.已知正四面体ABCD的棱长为2，平面α与棱AB，CD均平行，则α截此正四面体所得截面面积的最大值为

A.1     B.2     C.3     D.2

二、多项选择题：本题共4小题，每小题5分，共20分。在每小题给出的四个选项中，有多项符合题目要求。全部选对的得5分，部分选对的得2分，有选错的得0分。

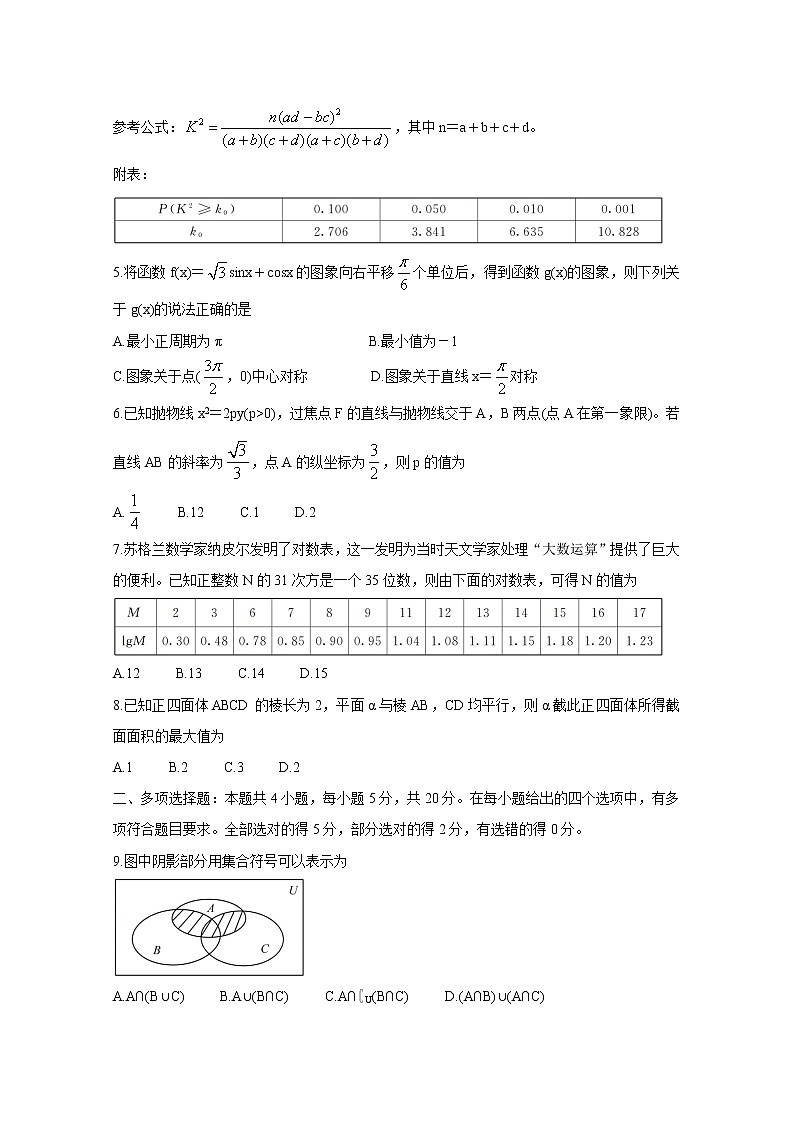
9.图中阴影部分用集合符号可以表示为

A.A∩(B∪C)     B.A∪(B∩C)     C.A∩∁U(B∩C)     D.(A∩B)∪(A∩C)

10.已知函数f(x)＝，则下列说法正确的是

A.f(x)为奇函数              B.f(x)为减函数

C.f(x)有且只有一个零点      D.f(x)的值域为[－1，1)

11.已知数列{an}中，a1＝1，an·an＋1＝2n，n∈N＋，则下列说法正确的是

A.a4＝4    B.{a2n}是等比数列    C.a2n－a2n－1＝2n－1    D.a2n－1＋a2n＝2n＋1

12.已知F1，F2分别为双曲线x2－＝1的左、右焦点，过F2且倾斜角为θ的直线与双曲线的右支交于A，B两点，记△AF1F2的内切圆O1的半径为r1，△BF1F2的内切圆O2的半径为r2，圆O1的面积为S1，圆O2的面积为S2，则

A.θ的取值范围是(，)       B.直线O1O2与x轴垂直

C.若r1＋r2＝2，则|AB|＝6         D.S1＋S2的取值范围是[2π，)

三、填空题：本题共4小题，每小题5分，共20分。

13.已知平面向量a，b，满足|b|＝，(a－b)⊥b，则a·b的值为            。

14.习近平总书记在党史学习教育动员大会上强调：“回望过往的奋斗路，眺望前方的奋进路，必须把党的历史学习好、总结好，把党的成功经验传承好、发扬好。”某党小组为响应习总书记号召，重温百年奋斗的恢弘史诗，以信仰之光照亮前行之路，组织开展党史学习教育知识竞赛活动，其中7名党员在这次活动中的成绩统计如图所示。则这7个成绩的中位数所对应的党员是            。

15.已知一个圆锥的侧面积是底面面积的2倍，则该圆锥的母线与其底面所成的角的大小为            。

16.已知函数f(x)＝ex－a－eln(ex＋a)，若关于x的不等式f(x)≥0恒成立，则实数a的取值范围为            。

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

17.(10分)

在△ABC中，角A，B，C的对边分别为a，b，c，已知△ABC恰好满足下列四个条件中的三个：①cosA＝；②cosB＝－；③a＝；④b＝1。

(1)请指出这三个条件(不必说明理由)；

(2)求边c。

18.(12分)

已知等差数列{an}的前n项和为Sn，且满足a2＝4，S5＝30。

(1)求{an}的通项公式；

(2)若bn＝，求数列{bn}的前n项和Tn。

19.(12分)

如图1，在等腰梯形ABCD中，E为CD的中点，AB＝BC＝CE，将△ADE，△BCE分别沿AE，BE折起，使平面ADE⊥平面ABE，平面BCE⊥平面ABE，得到图2。

(1)证明：AB∥CD；

(2)记平面ADE与平面BCE的交线为l，求二面角D－l－C的大小。

20.(12分)

已知函数fn(x)＝1＋x＋(n∈N＋)。

(1)证明：f3(x)单调递增且有唯一零点；

(2)已知f2n－1(x)单调递增且有唯一零点，判断f2n(x)的零点个数。

21.(12分)

已知椭圆C：的离心率为，且经过点H(－2，1)。

(1)求椭圆C的方程；

(2)过点P(－3，0)的直线与椭圆C相交于A，B两点，直线HA，HB分别交x轴于M，N两点，点G(－2，0)，若，，求证：为定值。

22.(12分)

某企业对生产设备进行优化升级，升级后的设备控制系统由2k－1(k∈N＋)个相同的元件组成，每个元件正常工作的概率均为p(0<p<1)，各元件之间相互独立。当控制系统有不少于k个元件正常工作时，设备正常运行，否则设备停止运行，记设备正常运行的概率为pk(例如：p2表示控制系统由3个元件组成时设备正常运行的概率；p3表示控制系统由5个元件组成时设备正常运行的概率)。

(1)若每个元件正常工作的概率p＝。

(i)当k＝2时，求控制系统中正常工作的元件个数X的分布列和期望；

(ii)计算p3。

(2)已知设备升级前，单位时间的产量为a件，每件产品的利润为1元，设备升级后，在正常运行状态下，单位时间的产量是原来的4倍，且出现了高端产品，每件产品成为高端产品的概率为，每件高端产品的利润是2元。请用pk表示出设备升级后单位时间内的利润y(单位：元)，在确保控制系统中元件总数为奇数的前提下，分析该设备能否通过增加控制系统中元件的个数来提高利润。