2021东北师大附中高三下学期第四次模拟考试数学（理）含答案

这是一份2021东北师大附中高三下学期第四次模拟考试数学（理）含答案，文件包含答案docx、试题docx等2份试卷配套教学资源，其中试卷共11页， 欢迎下载使用。
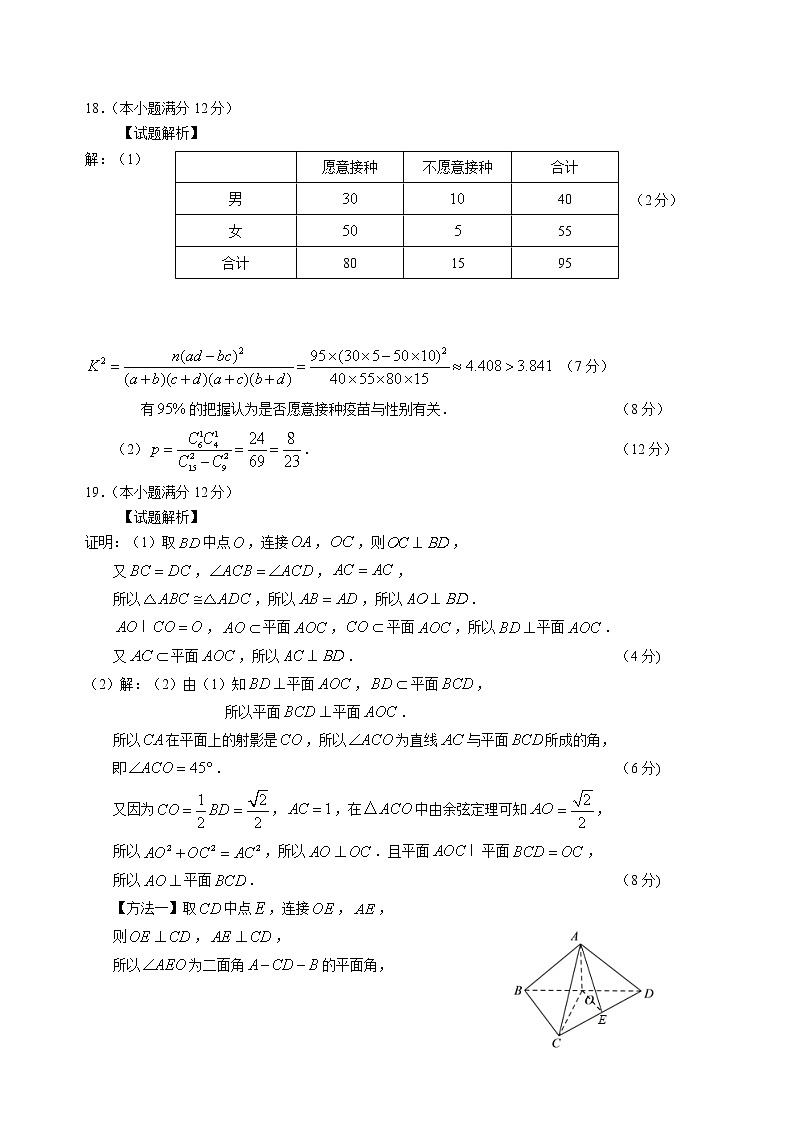
切磋砥砺足千日  紫电龙光助鹰扬东北师大附中 2018级高三年级 第四次模拟考试数学（理）学科试卷 本试卷共23题，共150分，共6页．注意事项：1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内．2．选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚．3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效．4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑．5．保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀．一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合，则 A．B． C． D．2．已知是两条不同的直线，是平面，，，则“”是“”的 A．充要条件      B．充分不必要条件 C．必要不充分条件    D．既不充分也不必要条件3．执行如图所示的程序框图，若输出的是，则判断框内的条件可以是 A．  B．  C．  D．4．若在上是减函数，则的最大值是 A．   B．   C．   D．5．若双曲线：的一条渐近线被以焦点为圆心的   圆所截得的弦长为，则 A．1   B．   C．   D．26．函数的图象大致为A．     B．     C．     D．7．某高中高一、高二、高三年级的人数分别为1200、900、900人．现按照分层抽样的方法抽取300名学生，调查学生每周平均参加体育运动的时间．样本数据（单位：小时）整理后得到如右图所示的频率分布直方图．下列说法错误的是A．每个年级抽取的人数分别为120、90、90人B．估计高一年级每周平均体育运动时间不足小时的人数约为人C．估计该校学生每周平均体育运动时间不少于小时的人数约为人D．估计该校学生每周平均体育运动时间不少于小时的百分比为8．已知的面积是（其中为的边长），则的形状   为 A．等边三角形      B．是直角三角形但不是等腰三角形  C．是等腰三角形但不是直角三角形  D．等腰直角三角形9．已知，则 A．   B．   C．   D． 10．人们很早以前就开始探索高次方程的数值求解问题．牛顿（Issac Newton,1643-1727）在《流数法》一书中给出了牛顿法—用“作切线”的方法求方程的近似解．如图，方程的根就是函数的零点，取初始值，在处的切线与轴的交点为，在处的切线与轴的交点为，一直继续下去，得到，它们越来越接近．若，则用牛顿法得到的的近似值约为 A．1.438   B．1.417   C．1.416    D．1.37511．已知，若方程有三个不同的解，且，    则的取值范围是 A．  B．  C．   D． 12．已知，，，则A． B．  C．   D．二、填空题：本题共4小题，每小题5分，共20分．13．已知为虚数单位，复数满足，则         ．14．若实数，满足约束条件，则的最大值为         ． 15．如图，在同一个平面内，向量与的夹角为，且，   向量与的夹角为，且，． 若=+（，），则         ． 16．如图①，用一个平面去截圆锥，得到的截口曲线是椭圆．许多人从纯几何的角度出发对这个问题进行过研究，其中比利时数学家Germinal dandelin(1794-1847)的方法非常巧妙，极具创造性．在圆锥内放两个大小不同的球，使得它们分别与圆锥的侧面，截面相切，两个球分别与截面相切于，在截口曲线上任取一点，过作圆锥的母线，分别与两个球相切于，由球和圆的几何性质，可以知道，，，于是．由的产生方法可知，它们之间的距离是定值，由椭圆定义可知，截口曲线是以为焦点的椭圆． 如图②，一个半径为的球放在桌面上，桌面上方有一个点光源，则球在桌面上的投影是椭圆．已知是椭圆的长轴，垂直于桌面且与球相切，，则椭圆的离心率为         ． 三、解答题：共70分．解答应写出文字说明、解答过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17.（12分）设等差数列公差为，等比数列公比为，已知，．（1）求数列和的通项公式； （2）求数列的前项和． 18．（12分） 近日，为进一步做好新冠肺炎疫情防控工作，某社区以网上调查问卷形式对辖区内部分居民做了新冠疫苗免费接种的宣传和调查．调查数据如下：共份有效问卷，名男性中有名不愿意接种疫苗，名女性中有名不愿意接种疫苗． （1）根据所给数据，完成下面的列联表，并根据列联表，判断是否有的把握认为是否愿意接种疫苗与性别有关？  愿意接种不愿意接种合计男   女   合计        （2）从不愿意接种的份调查问卷中得到拒绝接种新冠疫苗的原因：有份身体原因不能接种；有份认为新冠肺炎已得到控制，无需接种；有份担心疫苗的有效性；有份担心疫苗的安全性．求从这份问卷中随机选出份，在已知至少有一份担心疫苗安全性的条件下，另一份是担心疫苗有效性的概率．附：0.050    0.010     0.005  3.841    6.635     7.879     19．（12分） 如图，在三棱锥中，，，． （1）证明：； （2）若直线与平面所成的角为，，求二面角的余弦值．   20．（12分） 如图，已知抛物线的焦点为，四点都在抛物线上，直线与直线相交于点，且直线斜率为． （1）求和的值； （2）证明直线过定点，并求出该定点．21．（12分） 已知函数有两个极值点． （1）求的取值范围； （2）证明：．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，按所做的第一题计分．22. [选修：坐标系与参数方程]（10分）平面直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为. （1）写出曲线的极坐标方程和曲线的直角坐标方程； （2）若射线：平分曲线，且与曲线交于点（异于点），曲线上的点满足，求的面积.23. [选修：不等式选讲]（10分） 已知函数. （1）求的最大值； （2）已知，且，求证：.