2021新余高三下学期第二次模拟考试数学（理）试题含答案

新余市2020-2021学年度高三二模考试

数学试题卷（理科）

说明：1．本卷共有三个大题，23个小题，全卷满分150分,考试时间120分钟．

2．本卷分为试题卷和答题卷，答案要求写在答题卷上，在试题卷上作答不给分．

一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

1．已知集合，集合，则（   ）

A.      B．    C．   D．

2．若复数，（i为虚数单位），则的共轭复数为（   ）

A.           B．        C．       D．

3．某工厂生产了10000根钢管，其钢管内径(单位：)服从正态分布，工作人员通过抽样的方式统计出，钢管内径高于的占钢管总数的，则这批钢管内径在到之间的钢管根数约为（   ）

A.         B．            C．        D．

4．已知双曲线的一条渐近线方程为，且经过点，则双曲线的方程是（   ）

A.      B.     C.   D.

5．已知，则的大小关系（    ）

A.      B.     C.   D.

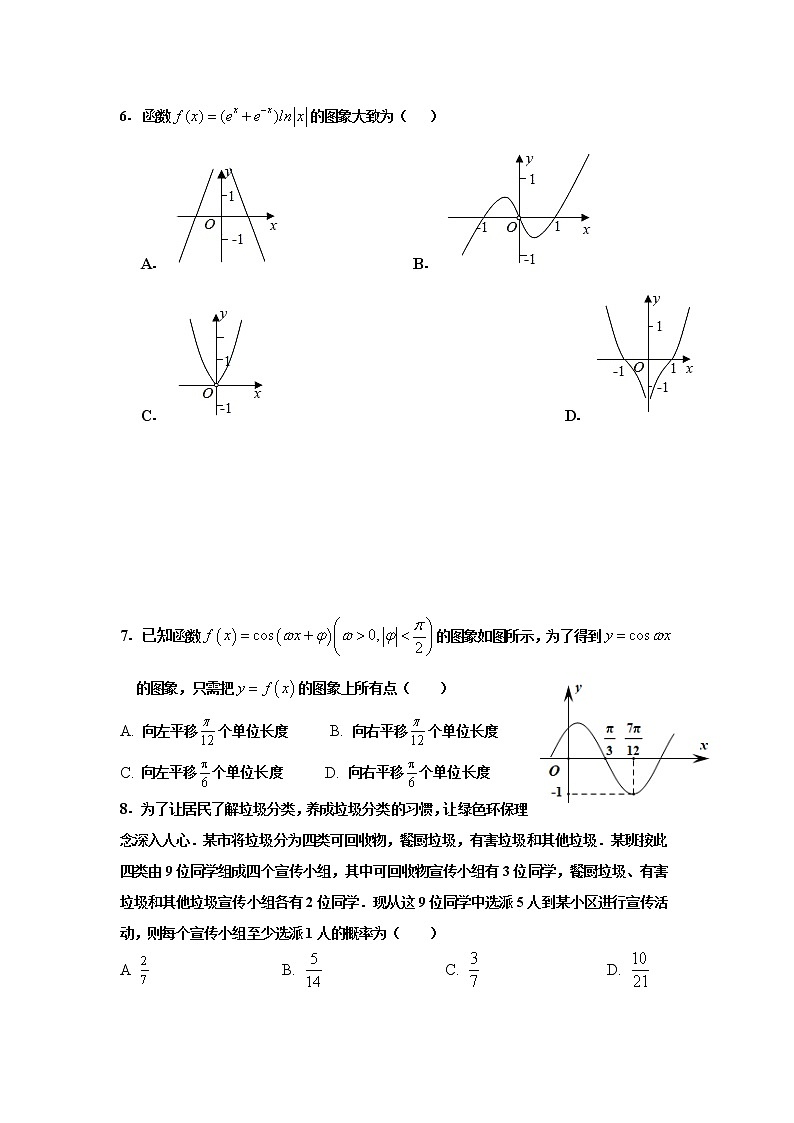
6．函数的图象大致为（   ）

A． B． 

C． D．

7．已知函数的图象如图所示，为了得到的图象，只需把的图象上所有点（    ）

A. 向左平移个单位长度      B. 向右平移个单位长度

C. 向左平移个单位长度      D. 向右平移个单位长度

8．为了让居民了解垃圾分类，养成垃圾分类的习惯，让绿色环保理念深入人心．某市将垃圾分为四类可回收物，餐厨垃圾，有害垃圾和其他垃圾．某班按此四类由9位同学组成四个宣传小组，其中可回收物宣传小组有3位同学，餐厨垃圾、有害垃圾和其他垃圾宣传小组各有2位同学．现从这9位同学中选派5人到某小区进行宣传活动，则每个宣传小组至少选派1人的概率为（    ）

A  B.  C.  D.

9．已知等差数列的第5项是展开式中的常数项，则该数列的前9项的和为（　  ）

A．           B．         C．         D．

10．如图，已知圆A，圆D的半径均为，，，均是边长为4的等边三角形.设点P为圆D上的一动点，的最大值为（　  ）

A. 18 B. 24 C. 36 D. 48

11．已知是椭圆：的左焦点，椭圆上一点关于原点的对称点为，若的周长为.则离心率（    ）

A.           B．           C.             D.

12．对于函数与，若存在，使，则称，是函数与图象的一对“隐对称点”.已知函数，，函数与的图象恰好存在两对“隐对称点”，则实数的取值范围为（    ）

A.      B．       C．      D．

二、填空题（本大题共4小题，每题5分，共20分.请将正确答案填在答题卷相应位置.）

13．已知向量，，，若，则实数＝______．

14．已知实数，满足约束条件，则的最大值为_______．

15．数列满足(，且)，，对于任意有恒成立，则的取值范围是___________.

16．在三棱锥中，则三棱锥外接球的表面积为______．     

三、解答题（本大题共6小题，共70分,解答应写出必要的文字说明、证明过程及演算步骤）

17．（本小题满分 12 分）

在中, 内角的对边分别为，,

点为边上一点, .

（1）求;   

（2）求的面积.

18．（本小题满分 12 分）

甲、乙两队进行排球比赛，每场比赛采用“5局3胜制”（即有一支球队先胜3局即获胜，比赛结束）．比赛排名釆用积分制，积分规则如下：比赛中，以或取胜的球队积3分，负队积0分；以取胜的球队积2分，负队积1分．已知甲、乙两队比赛，甲每局获胜的概率为．

（1）甲､乙两队比赛1场后，求甲队的积分X的概率分布列和数学期望；

（2）甲､乙两队比赛2场后，求两队积分相等的概率.

19．（本小题满分 12 分）

如图 在斜三棱柱中，是边长为的正三角形，侧棱，顶点在面的射影为边的中点 .

（1）求证：面面；

（2）求面与面所成锐二面角的余弦值.

20．（本小题满分 12 分）

已知抛物线上一点，圆，过点引圆的两条切线，与抛物线分别交于，两点，与圆的切点分别为， .

（1）当时，求所在直线的方程；

（2）记线段 的中点的横坐标为，求的取值范围.

21．（本小题满分 12 分）

已知函数.

（1）求曲线在点处的切线方程；

（2）时，判断函数存在极值点的个数，并说明理由.

选考题：（本小题满分 10 分）.

请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.

22．选修4-4：坐标系与参数方程

在平面直角坐标系中，曲线的参数方程为（为参数，且，），以坐标原点为极点，轴的正半轴为极轴建立极坐标系.

（1）求曲线的极坐标方程；

（2）设曲线的极坐标方程为，若直线与曲线交于两点，直线与曲线交于两点，在第一象限，求.

23．[选修4-5：不等式选讲]（本小题满分10分）

已知不等式的解集为．

（1）求m，n的值；

（2）若，，求证：．

数学（理科）答案

一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

1. B     2.A．   3.C      4.C.       5．C        6. D

7.A     8.D     .9.D.     10. C.      11．A.      12.D.

二、填空题（本大题共4小题，每题5分，共20分.请将正确答案填在答题卷相应位置.）

13.﹣3        14..      15．      16.        

三、解答题（本大题共6小题，共70分,解答应写出必要的文字说明、证明过程及演算步骤）

17．（本小题满分 12 分）

解：（1）已知，

用正弦定理得:

（2）在中用余弦定理得

又

18．（本小题满分 12 分）

解：（1）依题意，X的所有可能取值为0，1，2，3，且

，

，

，

，.....................................................4分

所以X的概率分布列为

所以......................................................6分

（2）记“甲､乙比赛两场后，两队积分相等”为事件A.

设第i场甲､乙两队积分分别为，则，.

因为两队积分相等，所以，

即，所以............................................9分

所以

答：甲､乙比赛两场后，两队积分相等的概率为............................................12分

19．（本小题满分 12 分）

【解析】

【详解】（1）证明：且为中点，，

又面，面，所以，

，故面，

而面，因此，面面；..........................................5分

（2）平面，，以点为坐标原点，、、所在直线分别为、、轴建立如下图所示的空间直角坐标系，

因为，，所以，

由条件可得、、，从而，，

设面的法向量为，由，得，

取，则，，可得，

易知面的一个法向量，.....................................................................10分

，

故面与面所成锐二面角的余弦值为...........................................12分

20．（本小题满分 12 分）

解：（1）由条件知M(4,0)，以线段PM为直径的圆的方程为，

而，两圆相减得：，即为所在直线的方程；............................................................................................................................................5分

（2）由题意知切线PA、PB的斜率存在，分别设，于是切线PA、PB的方程分别为，。设,则点M(4,0)到切线PA的距离为，两边平方整理得：，

同理可得，.........................................................7分

于是可知是方程的两个实根，则又所以，联立消，整理得，显然，韦达定理可知所以

同理：于是.......................................................................................................10分

的取值范围............................................................................................................12分

21．（本小题满分 12 分）

解：（1）由，而则曲线在点处的切线方程为

化为：...............................................................................................................................4分

(2)由于，..........................5分

令

其中，又图像为开口向下的抛物线，

所以必定存在使，且易知：时，即故在上单调递增；时，即故在上单调递减，

又因为，则可知必有，所以时，，单调递增；时，，单调递减，则是函数极大值点，............................................................................................................................................10分

取知则，那么，由零点存在性定理知必有，使得，且时，，单调递减；时，，单调递增，则是函数极小值点，

（用极限说明零点存在性请酌情给分）

综上所述：时，函数存在极值点的个数为2个。.........................................12分

选考题：（本小题满分 10 分）.

请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.

22．选修4-4：坐标系与参数方程

在平面直角坐标系中，曲线的参数方程为（为参数，且，），以坐标原点为极点，轴的正半轴为极轴建立极坐标系.

（1）求曲线的极坐标方程；

（2）设曲线的极坐标方程为，若直线与曲线交于两点，直线与曲线交于两点，在第一象限，求.

【答案】（1）；（2）

【详解】

⑴化简曲线的参数方程得，（为参数，且，）

消去参数得曲线的普通方程.  ...............................................3分

化成极坐标方程为，

                       .............................5分

⑵ 易知直线极坐标方程为，代入.    得：，

而在第一象限，在第三象限，因此：......................................10分

23．[选修4-5：不等式选讲]（本小题满分10分）

已知不等式的解集为．

（1）求m，n的值；

（2）若，，求证：．

【解答】（Ⅰ）解：原不等式化为或或，

解得﹣1＜x≤0或0＜x＜1或1≤x＜5，

取并集，可得原不等式的解集为（﹣1，5），

又不等式|x|+|x﹣1|＜x+4的解集为（m，n），

∴m＝﹣1，n＝5；                                  ...........................................5分

（Ⅱ）证明：由（Ⅰ）及（n﹣1）x+y+m＝0，可得（5﹣1）x+y﹣1＝0，即4x+y＝1，

∴＝5+，

当且仅当x＝，y＝时取“＝”．

∴x+y≥9xy．                                   ...........................................10分