2021上饶高三下学期3月第二次高考模拟考试（二模）数学（理）试题含答案

这是一份2021上饶高三下学期3月第二次高考模拟考试（二模）数学（理）试题含答案，文件包含上饶市2021届二模理科数学答案docx、上饶市2021届二模理科数学试卷docx等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
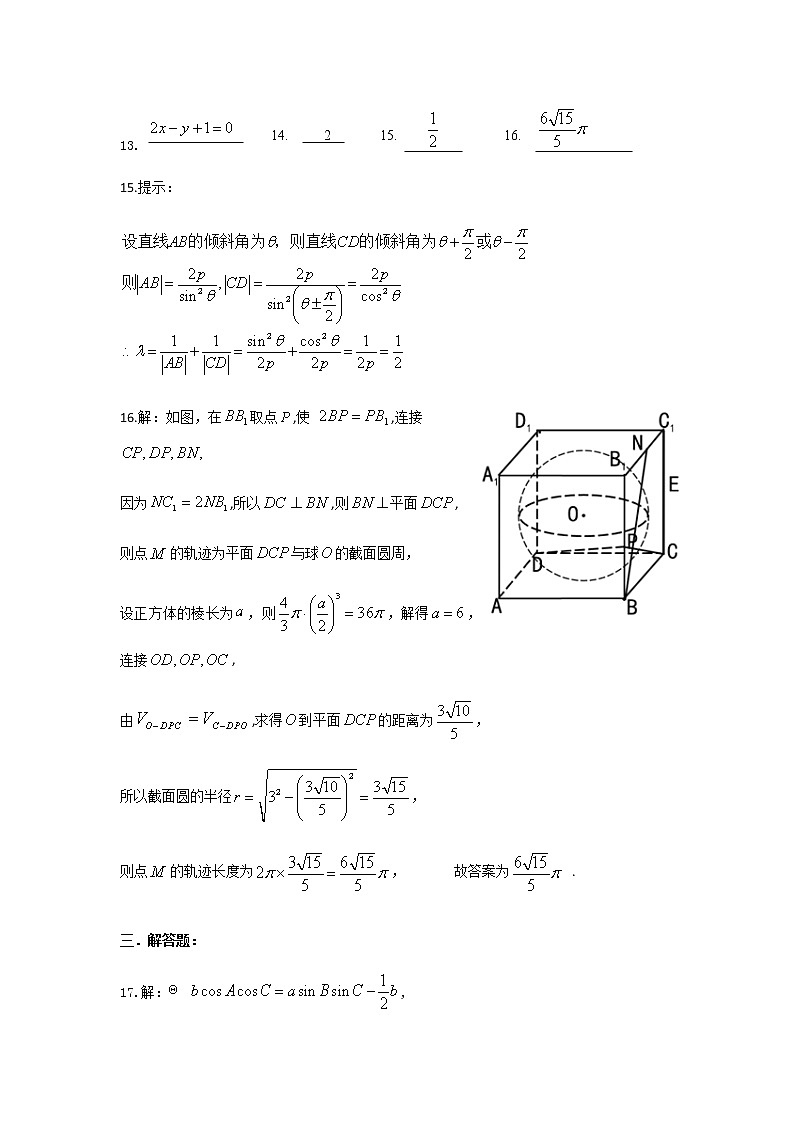
上饶市2021届第二次高考模拟考试数学（理科）答案 一、选择题123456789101112ADCDDCDDBBDA提示：因为点在平面内绕点作圆周运动，并且始终保持，所以，又因为，为定值，所以也是定值，所以点在某个定球面上运动，故A正确；作出简图如下，所以，故B正确；易知C正确；当AB在平面内时，直线与平面所成角最小，等于，所以直线与平面 所成角的余弦值的最大值为1，故D不正确.提示：解：如图所示，根据题意可设，则，,二．填空题     14.     2       15.             16.        15.提示：16.解：如图，在取点,使 ,连接因为,所以,则平面,则点的轨迹为平面与球的截面圆周，设正方体的棱长为，则，解得，连接,由,求得到平面的距离为，所以截面圆的半径，则点的轨迹长度为，       故答案为 .三．解答题：17.解： ,, ……………………………1分因为.所以，即，…………3分因为，所以，即，因为.所以. …………………………………………6分（1）若选①，②，   ………………………………8分即，              ………………………………10分所以的面积  .………………12分（2）若选②，③由,得                       又                     ………………………………9分所以的面积.………………12分（3）若选①，③由,得， ………………………8分              即，      ………………………………10分所以的面积. ………………12分解：（1）根据题意，学员1，2，4，6恰有两项不合格，从中任意抽出人，所有可能的情况如下：项目学员补测编号项数（1）（2）②③⑤3（1）（4）②③④⑤4（1）（6）③④⑤3（2）（4）②④⑤3（2）（6）②③④⑤4（4）（6）②③④3由表可知，全部6种可能的情况中，有4种情况补测项目种类不超过，故所求概率为；……………………………………………………………4分（2）由题意可知，学员甲在每轮测试(或补测)中通过的概率为：①由题意，若学员甲没通过“科二”考试，当且仅当其第1轮考试与次补测均未能完成项测试，相应概率为，故学员甲能通过“科二”考试的概率为，……………………………………8分②根据题意，当且仅当该学员通过第一轮考试，或未通过第一次考试但通过第轮补测时，，其他情况时均有，…………………………10分故的分布列为：故………………………………………………12分解：（1）∵正△ABC的边长为3，且，△ADE中，∠DAE＝60°，由余弦定理，得DE，∵AE2+DE2＝4＝AD2，∴DE⊥AE．……………………………………………………3分折叠后，仍有A1E⊥DE．∵二面角A1﹣DE﹣B成直二面角，∴平面A1DE⊥平面BCDE，又∵平面A1DE∩平面BCDE＝DE，A1E⊂平面A1DE，A1E⊥DE，∴A1E⊥平面BCED；…………………………………6分（2）假设在线段BC上存在点P，使直线PA1与平面A1EC所成的角为60°．如图，建立空间直角坐标系. 作，设则，，故，又………………………………………………8分，又平面A1EC的法向量…………………………………10分所以存在这样的点P，且.……………………………………………12分（1） 因为动点P在曲线C上运动且保持的值不变，且点G在曲线C上，的轨迹是以A、B为焦点的椭圆，………………………………………………3分且，所以曲线C的方程为…………………………………………………5分（2）设，，，得， …………………………………………………………7分由于点M在椭圆上，故               整理得同理可得……………………………………10分是方程的两个根…………………………………12分.解：（1），定义域为..…………………………1分由，解得，可得解得.      …………………………2分由，解得，可得解得.                    …………………………3分的单调递增区间为，单调递减区间为.                       …………………………4分（2）由已知，，令，则.，当时，；当时，，在上单调递增，在上单调递减，即在上单调递增，在上单调递减. …………………………6分①当时，即时，， ，使得，当时，；当时，，在上单调递增，上单调递减. ， .又 ，由零点存在性定理可得，此时在上仅有一个零点.   ……………………8分                                             ②若时，，又在上单调递增，在上单调递减，而， ，，使得，，且当、时，；当时，.在和上单调递减，在上单调递增.，.，.又，由零点存在性定理可得，在和内各有一个零点，即此时在上有两个零点.                  ……………………11分 综上所述，当时，在上仅有一个零点；当时，在上有两个零点.                                     ……………………12分 22.（本小题满分10分）[选修4-4：坐标系与参数方程]解：（1）曲线，…………………………3分曲线………………………………5分（没注明扣1分）（2） 由 得.……………………………6分    由得………………………………7分               又，当时，……………………………10分23.（1）若，不等式即，则或或，解得或或，故原不等式的解集为；……………………………………………………5分（2）由，得，设，，在平面直角坐标系中做出的大致图像，如图所示，结合图像分析，可知当，即时，、的图像有三个不同的交点，故函数恰有三个零点时，实数的取值范围是.…………………10分