2021宝鸡金台区高二下学期期中考试数学（文）试题选修1-2含答案

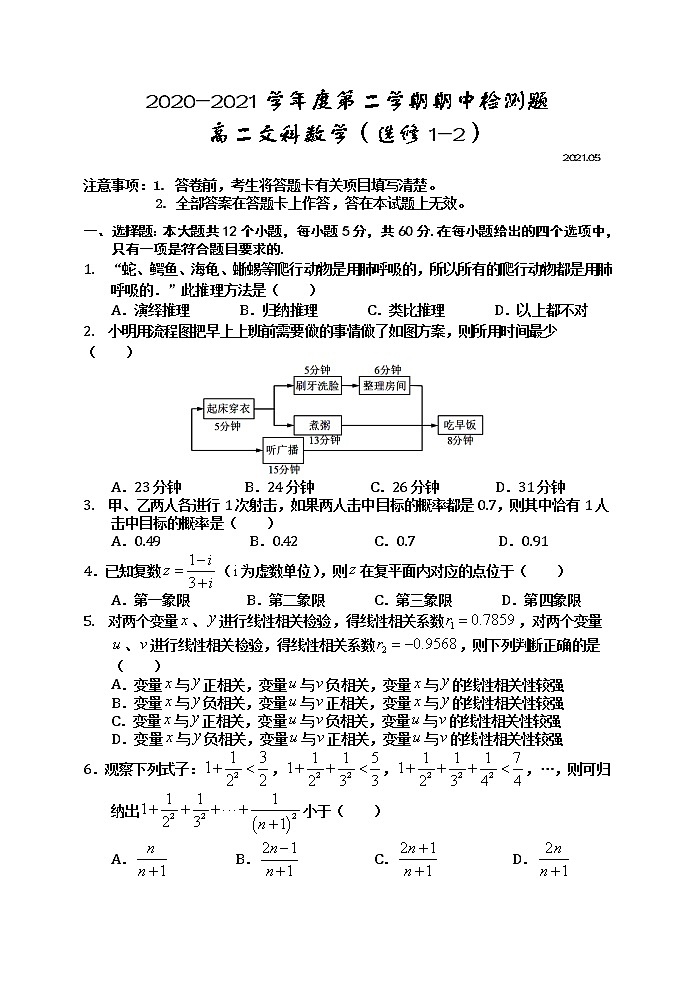
2020-2021学年度第二学期期中检测题

高二文科数学（选修1-2）

              2021.05

注意事项：1. 答卷前，考生将答题卡有关项目填写清楚。

          2. 全部答案在答题卡上作答，答在本试题上无效。

一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1.  “蛇、鳄鱼、海龟、蜥蜴等爬行动物是用肺呼吸的，所以所有的爬行动物都是用肺呼吸的．”此推理方法是（    ）

A．演绎推理       B．归纳推理       C．类比推理       D．以上都不对

2.  小明用流程图把早上上班前需要做的事情做了如图方案，则所用时间最少（    ）

A．23分钟         B．24分钟        C．26分钟        D．31分钟

3.  甲、乙两人各进行1次射击，如果两人击中目标的概率都是0.7，则其中恰有1人击中目标的概率是（    ）

A．0.49 B．0.42    C．0.7 D．0.91

4．已知复数（为虚数单位），则在复平面内对应的点位于（    ）

A．第一象限        B．第二象限       C．第三象限       D．第四象限

5.  对两个变量、进行线性相关检验，得线性相关系数，对两个变量、进行线性相关检验，得线性相关系数，则下列判断正确的是（    ）

A．变量与正相关，变量与负相关，变量与的线性相关性较强

B．变量与负相关，变量与正相关，变量与的线性相关性较强

C．变量与正相关，变量与负相关，变量与的线性相关性较强

D．变量与负相关，变量与正相关，变量与的线性相关性较强

6．观察下列式子：，，，…，则可归纳出小于（    ）

A． B． C． D．

7．否定“自然数中恰有一个偶数”的正确的反设为（   ）

A．都是奇数 B．都是偶数

C．至少有两个偶数         D．中或都是奇数或至少有两个偶数

8．为迎接学校的文艺汇演，某班准备编排一个小品，需要甲、乙、丙、丁四位同学扮演老师、家长、学生、快递员四个角色，他们都能扮演其中任意一个角色，下面是他们选择角色的一些信息：①甲和丙均不扮演快递员，也不扮演家长；②乙不扮演家长；③如果甲不扮演学生，那么丁就不扮演家长．若这些信息都是正确的，由此推断丙同学选择扮演的角色是（    ）

A．老师          B．家长         C．学生            D．快递员

9. 已知，，则等于（    ）

A． B． C． D．

10．宋元时期，中国数学鼎盛时期中杰出的数学家有“秦﹝九韶﹞、李﹝冶﹞、杨﹝辉﹞、朱﹝世杰﹞四大家”，朱世杰就是其中之一．朱世杰是一位平民数学家和数学教育家．朱世杰平生勤力研习《九章算术》，旁通其它各种算法，成为元代著名数学家．他全面继承了前人数学成果，既吸收了北方的天元术，又吸收了南方的正负开方术、各种日用算法及通俗歌诀，在此基础上进行了创造性的研究，写成以总结和普及当时各种数学知识为宗旨的《算学启蒙》，其中有关于“松竹并生”的问题：松长四尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．如图，是源于其思想的一个程序框图．若输入的分别为，，则输出的（    ）

A．2               B．3

C．4               D．5

11．如图所示，个连续自然数按规律排列如下：

根据规律，从2014到2016的箭头方向依次为（    ）

A．→↑           B．↑→     

C．↓→           D．→↓

12．魏晋时期数学家刘徽首创割圆术，他在《九章算术》方田章圆田术中指出：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣.”这是注述中所用的割圆术是一种无限与有限的转化过程，比如在正数中的“”代表无限次重复，设，则可以利用方程求得，类似地可得到正数（    ）

A．2 B．3 C． D．

二、填空题：本大题共4小题，每小题5分，共20分.（注：16题前三空每空1分，第四空2分）

13．___________．

14．已知由一组样本数据确定的回归直线方程为，且，发现有两组数据与误差较大，去掉这两组数据后，重新求得回归直线的斜率为1，那么当时，的估计值为___________．

15．已知甲在上班途中要经过两个路口，在第一个路口遇到红灯的概率为，两个路口连续遇到红灯的概率为，则甲在第一个路口遇到红灯的条件下，第二个路口遇到红灯的概率为___________．

16．已知数列满足，，且，则________，  ________，________，猜想_________．

三、解答题：本大题共4小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17.（本小题满分17分）

设，用综合法证明：.

18.（本小题满分18分）

这次新冠肺炎疫情，是新中国成立以来在我国发生的传播速度最快、感染范围最广防控难度最大的一次重大突发公共卫生事件.中华民族历史上经历过很多磨难，但从来没有被压垮过，而是愈挫愈勇，不断在磨难中成长，从磨难中奋起.在这次疫情中，全国人民展现出既有责任担当之勇、又有科学防控之智，某市某校学生也运用数学知识展开了对这次疫情的研究，一名同学在疫情初期数据统计中发现，从2020年2月1日至2月7日期间，日期和全国累计报告确诊病例数量（单位：万人）之间的关系如下表：

（1）根据表中的数据，适宜作为确诊病例数量关于日期的回归方程类型，请求出此线性回归方程；（精确到0.01）

（2）预测2月16日全国累计报告确诊病例数.（精确到0.01）

参考数据：①；②. 其中，.

参考公式：对于一组数据，，…，其回归方程中斜率和截距的最小二乘估计公式分别为：①，②.

19.（本小题满分18分）

2019年4月，江苏省发布了高考综合改革实施方案，试行“”高考新模式.为调研新高考模式下，某校学生选择物理或历史与性别是否有关，统计了该校高三年级800名学生的选科情况，部分数据如下表：

（1）根据所给数据完成上述表格，并判断是否有99.9%的把握认为该校学生选择物理或历史与性别有关；

（2）该校为了提高选择历史科目学生的数学学习兴趣，用分层抽样的方法从该类学生中抽取5人，组成数学学习小组.一段时间后，从该小组中抽取2人汇报数学学习心得.求这2人均为男生的概率.

附：

20.（本小题满分17分） 

某同学在研究相邻三个整数的算术平方根之间的关系时，发现以下三个式子均是正确的：①； ②； ③.

（1）已知，，，请从以上三个式子中任选一个，结合此范围验证其正确性(注意不能近似计算)；

（2）请将此规律推广至一般情形，并加以证明.

高二数学文科选修1-2检测试题答案

一、选择题：本大题共12个小题，每小题5分，共60分。

1.B根据教材55页归纳推理的概念改编.

2. C根据教材40页练习2改编.

【详解】根据题干分析，要使所用的时间最少，可设计如下：起床穿衣—煮粥—吃早餐，所用时间为：（分钟）.故选C.

3. B根据教材19页例1改编.

【详解】两人都击中概率，都击不中的概率，∴恰有一人击中的概率．故选：B

4．D根据教材82页B组练习1改编.

【详解】因为，

所以在复平面内对应的点位于第四象限，故选：D

5．C 根据教材第7页相关系数概念改编.

【详解】由线性相关系数知与正相关，

由线性相关系数知与负相关，又，所以，变量与的线性相关性比与的线性相关性强，故选：C.

6．C根据教材57页课后练习题第2题改编.

【详解】由已知式子可知所猜测分式的分母为，分子是第个正奇数，即，

.故选：C.

7．D根据教材66页例4改编.

【详解】因为反证法中的反设就是原命题的否定，

而“自然数中恰有一个偶数”的否定是“中或都是奇数或至少有两个偶数”，

所以否定“自然数中恰有一个偶数”的正确的反设为“中或都是奇数或至少有两个偶数”，故选D.

8．A根据教材演绎推理方法改编.

【详解】因为甲和丙均不扮演快递员，也不扮演家长，乙不扮演家长，因此丁一定扮演家长．如果甲不扮演学生，那么丁就不扮演家长，即丁扮演家长，甲就扮演学生，又每人扮演一个角色，每个角色由一个人扮演，丙不扮演快递员，因此丙同学选择扮演的角色是老师.故选：A

9. D根据教材82页B组练习3改编.

【详解】设，则，

所以，解得，，即.故选：D

10. C根据教材42页例4改编.

【详解】输入的分别为，时，依次执行程序框图可得：

，，不成立，

，，不成立，

，，不成立，

，，成立，输出.故选C

11．B 根据选修1-2教材教师用书测试题改编.

【详解】由题意可知箭头变化的周期为，，故从2014到2016的箭头方向与从到的箭头方向一致，依次为↑→故选：B

12．A根据教材56页类比推理的概念及例5改编.选A

【详解】设，则且，所以，所以，所以，所以或（舍）.所以.故选：A

二、填空题：本大题共4小题，每小题5分，共20分。

13．根据教材81页A组练习3改编.

【详解】.

14．根据教材回归分析的概念改编.

【详解】，，

由题意知：去掉两组数据和后，样本中心点没变，

设重新求得的回归直线方程为，将样本点的中心代入，

解得：，即当时，.

故答案为：.

15．  根据教材17页例题改编.

【详解】设事件A：第一个路口遇到红灯，事件B：第二个路口遇到红灯，

则，，，

故答案为：.

16．根据教材54页例2改编.答案：3    4    5       

【详解】当时，，

当时，；

当时，，

所以，故猜想 .

数学归纳法证明：

当，，显然满足，

假设当时，成立，

则当时，，

故当时，通项公式满足；综上，.

故答案为：；；；.

三、解答题：本大题共4小题，共70分.

17.根据教材60页例3及64页习题3-3第2题改编.

【证明】因为，              ………3分

所以，  ………6分

所以，               ………9分

所以.   ①           ………12分

同理可得：    ②       ………14分

  ③       ………16分

所以

.

所以原不等式成立.                          ………17分

18．根据教材页例题改编.

（1）；（2）6.6万人.

【详解】（1）由已知数据得：，，  ………4分

∴，    ………7分

，            ………10分

所以，关于的回归方程为：；            ………12分

（2）把代入回归方程得：，   ………16分

所以预测2月16日全国累计报告确诊病例数为6.6万人.     ………18分

19．根据教材26页例3改编.

【详解】（1）

………5分

因为，………9分

所以有99.9%的把握认为该校学生选择物理或历史与性别有关.             ………10分

（2）按照分层抽样的方法，抽取男生2人，女生3人.设2名男生和3名女生分别为：，                ………12分

则所有抽取结果有共10种，                               ………16分

均为男生只有一种，所以概率为.      ………18分

20．根据教材62页例5改编.

【详解】（1）验证①式成立：

∵<1.74，∴<2.74.          ………3分

∵>1.41，∴>2.82，            ………6分

∴.                     ………7分

同理可验证②③正确.

说明：若用分析法证明（不用近似计算），也认为是对的.

（2）一般结论为:若n∈N*，则.         ………10分

证明：要证，

只需证，                        ………12分

即证 ，即证，  ………14分

只需证，即证0<1，显然成立，           ………16分

故.                                  ………17分