江苏省无锡市宜兴市2021-2022学年八年级下学期期末数学试题（含答案）

宜兴市初中2022年春学期期终调研试卷

八年级数学2022.06

本试卷分试题和答题卡两部分，所有答案一律写在答题卡上.

考试时间为120分钟，试卷满分150分.

注意事项：

1.答卷前，考生务必用0.5毫米黑色墨水签字笔将自己的姓名、班级、考试号填写在答题卡的相应位置上，并认真核对姓名、班级、考试号是否与本人的相符合.

2.答题必须用0.5毫米黑色墨水签字笔作答，写在答题卡上各题目指定区域内相应的位置，在其他位置答题一律无效.

3.作图必须用2B铅笔作答，并请加黑加粗，描写清楚.

4.卷中除要求近似计算的结果取近似值外，其他均应给出精确结果.

一、选择题（本大题共10小题，每题3分，共计30分.在每小题所给出的四个选项中，恰有一项是符合题目要求的，请把正确选项前的字母代号填涂在答题卡相应位置上.）

1.下列计算正确的是（    ）

A.   B.   C.   D.

2.下面四个图标中，中心对称图形个数是（    ）

A.0个   B.1个   C.2个   D.3个

3.下列说法正确的是（    ）

A.去年某中学有518名考生参加中考，为了了解这些考生的数学成绩，从中抽取50名考生的数学成绩进行统计分析，其中这50名考生是样本

B.某彩票的中奖机会是1%，买100张一定会中奖

C.从装有3个红球和4个黑球的袋子里摸出1个球是红球的概率是

D.对运载火箭的零部件进行检查应采用普查调查方式

4.已知等边三角形的边长为2，则其面积是（    ）

A.   B.   C.   D.4

5.下列命题是真命题的是（    ）

A.对角线相等的四边形是平行四边形

B.对角线互相平分且相等的四边形是矩形

C.对角线互相垂直的四边形是菱形

D.对角线互相垂直平分的四边形是正方形

6.反比例函数的图象与一次函数的图象交于点，则的值是（    ）

A.3   B.-3   C.-1   D.1

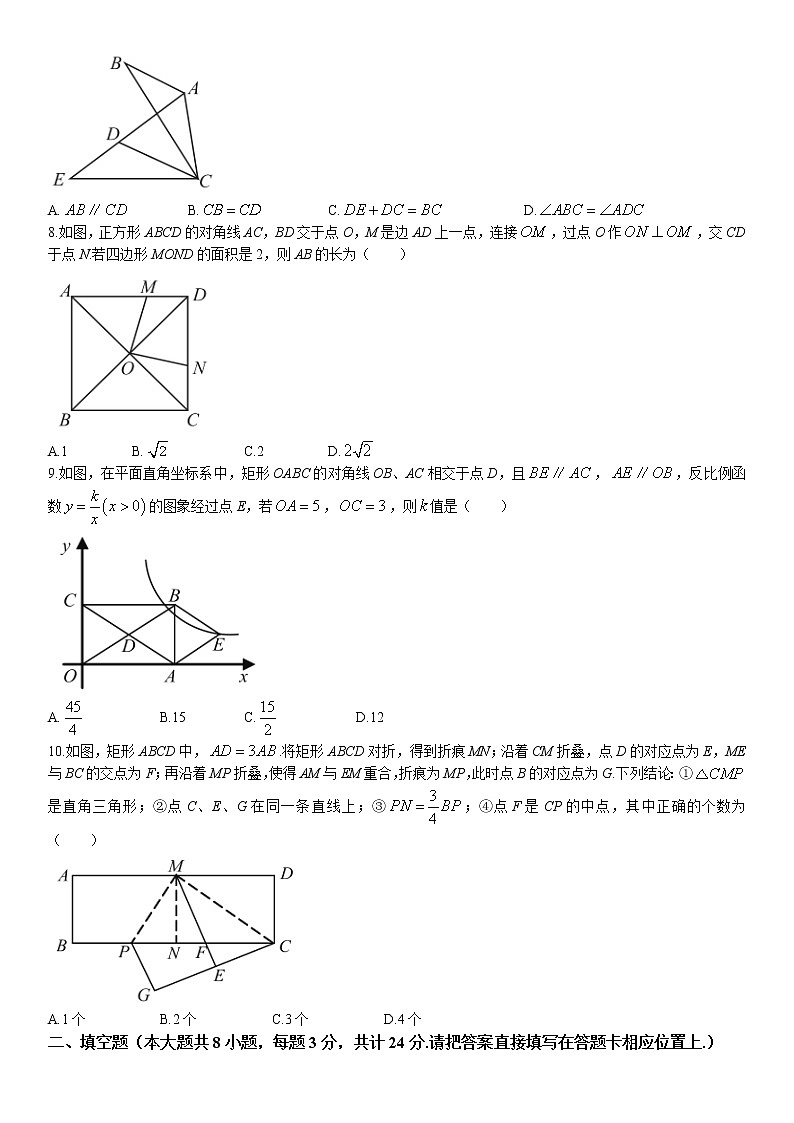
7.如图，在中，，将绕点C逆时针旋转得到，点A，B的对应点分别为D，E，连接AD.当点A，D，E在同一条直线上时，下列结论一定正确的是（    ）

A.   B.   C.   D.

8.如图，正方形ABCD的对角线AC，BD交于点O，M是边AD上一点，连接，过点О作，交CD于点N.若四边形MOND的面积是2，则AB的长为（    ）

A.1   B.   C.2   D.

9.如图，在平面直角坐标系中，矩形OABC的对角线OB、AC相交于点D，且，，反比例函数的图象经过点E，若，，则值是（    ）

A.   B.15   C.   D.12

10.如图，矩形ABCD中，.将矩形ABCD对折，得到折痕MN；沿着CM折叠，点D的对应点为E，ME与BC的交点为F；再沿着MP折叠，使得AM与EM重合，折痕为MP，此时点B的对应点为G.下列结论：①是直角三角形；②点C、E、G在同一条直线上；③；④点F是CP的中点，其中正确的个数为（    ）

A.1个   B.2个   C.3个   D.4个

二、填空题（本大题共8小题，每题3分，共计24分.请把答案直接填写在答题卡相应位置上.）

11.若分式的值为0，则____________.

12.在一个不透明袋子里装有4个黄球和2个红球，这些球除颜色外完全相同.从袋中任意摸出2个球都是红球，则这个事件是____________事件（填“随机”或“必然”或“不可能”）

13.在函数中，自变量的取值范围是_____________.

14.当时，函数的值随增大而增大，则的取值范围是____________.

15.如图，在矩形ABCD中，对角线AC、BD相交于点，，，则的周长为____________.

16.关于的分式方程的解为正整数，则满足条件的整数的值为____________.

17.如图，过原点的直线交反比例函数图象于P、Q点，过点Р分别作x轴，y轴的垂线，交反比例函数的图象于A、B点，已知，则图中阴影部分的面积为_____________；且当时，的值为_____________.

18.如图，正方形ABCD中，，连接AC，的平分线交AD于点E，在AB上截取，连接DF，分别交CE，AC于点G，H，点Р是线段GC上的动点，于点Q，连接PH，则__________；的最小值是___________.

三、解答题（本大题共10小题，共计96分.解答需写出必要的文字说明或演算步骤.）

19.计算：（本题满分8分）

（1）；

（2）

20.（本题满分8分）

（1）先化简，再求值：，其中，

（2）解分式方程：.

21.（本题满分10分）

国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》指出，要加强中小学生作业、睡眠、手机、读物、体质管理.某校数学社团成员采用随机抽样的方法，抽取了八年级部分学生，对他们一周内平均每天的睡眠时间t（单位：h）进行了调查，将数据整理后得到下列不完整的统计图表：

请根据图表信息回答下列问题：

（1）频数分布表中，___________，___________；

（2）扇形统计图中，C组所在扇形的圆心角的度数是____________；

（3）请估算该校1200名八年级学生中睡眠不足7小时的人数；

（4）研究表明，初中生每天睡眠时长低于7小时，会严重影响学习效率.请你根据以上调查统计结果，向学校提出一条合理化的建议.

22.（本题满分10分）

如图，在中，点E、F为对角线BD的三等分点，连结AE，CF，AF，CE.

（1）求证：；

（2）求证：四边形AECF为平行四边形.

23.（本题满分10分）

如图，正比例函数的图象与反比例函数的图象有一个交点为.

（1）求反比例函数函数表达式；

（2）根据图象，直接写出当-时，反比例函数的取值范围；

（3）根据图象，直接写出当时，自变量的取值范围.

24.（本题满分10分）

（1）如图1，点A、B都在边长为1的网格纸的格点上，仅用无刻度的直尺按要求画图.画出以AB为一边的平行四边形ABCD，使其四个顶点都在格点上，且；并直接写出平行四边形ABCD的周长=_____________，面积=_____________.

（2）如图2，已知，用无刻度的直尺和圆规在AB上作一点P，使得.（不写作法，保留作图痕迹）

25.（本题满分10分）

国庆节前，某超市为了满足人们的购物需求，计划购进甲、乙两种水果进行销售.经了解，乙种水果的进价比甲种水果的进价多5元，售价如下表所示：

已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.

（1）求甲、乙两种水果的进价；

（2）若超市购进这两种水果共150千克，其中甲种水果的重量不低于乙种水果重量的2倍，则超市应如何进货才能获得最大利润，最大利润是多少?

26.（本题满分10分）

如图，正方形ABCD中，在边CD的右侧作等腰三角形DCE，使，记为，连接AE，过点D作，垂足为G，交EC的延长线于点F，连接AF，作于H.

（1）①求的大小（用的代数式表示）；

②判断的形状，并说明理由.

（2）当，时，求CH的长.

27.（本题满分10分）

如图，在平面直角坐标系中，菱形ABCD的顶点D在第二象限，其余顶点都在第一象限，轴，，.过点A作，垂足为E，.反比例函数的图象经过点E，与边AB交于点F，连接OE，OF，EF.

（1）求的值

（2）若，求反比例函数关系式.

28.（本题满分10分）

已知结论：在直角三角形中，30°角所对的直角边是斜边的一半，请利用这个结论进行下列探究活动.如图，在中，，，，D为AB中点，P从A点出发，沿AC以每秒1个单位长度的速度向C运动，设Р点运动时间为t秒.连接PD，把沿PD翻折得到，连接CE.

（1）当时，__________.

（2）当以A、P、E、D为顶点的四边形是平行四边形时，求出t的值.

（3）在Р点运动过程中，是否存在以B、C、E、D为顶点的四边形是平行四边形?若存在，请求出t的值；若不存在，请说明理由.

2021-2022学年初二数学第二学期期末参考答案与评分标准

一、选择题（本大题共10小题，每小题3分，共30分.）

1.D  2.C  3.D  4.A  5.B  6.B  7.A  8.D  9.A  10.C

二、填空题（本大题共8小题，每小题3分，共24分.）

11.3  12.随机 13.14.15.9  16.-3  17.6，18.

三、解答题（本大题共8小题，共96分.）

19.（本题满分8分）

解：（1）原式

（2）原式

20.（本题满分8分）

（1）原式

（2）去分母得：

得，解得，

经检验，是分式方程的增根，

故此方程无解.

21.（本题满分10分）

解：（1）0.2，7；

（2）72；

（3）288人；

（4）建议学校尽量让学生在学校完成作业，课后少布置作业.

22.（本题满分10分）

证明：（1）∵四边形ABCD是平行四边形，

∴，，∴，

∵点E、F为对角线BD的三等分点，∴，

在△ABE和△CDF中，

∴△ABE≌△CDF（SAS），

（2）由（1）得△ABE≌△CDF，

∴AE=CF，∠AEB=∠CFD，∴∠AEF=∠CFE，∴AE∥CF，

∴四边形AECF是平行四边形；

23.（本题满分10分）

解：（1）将点代入，得，∴，∴，

∴反比例函数表达式为；

（2）的取值范围是；

（3）或.

24.（本题满分10分）

解：，10

25.（本题满分10分）

解：（1）设甲种水果的进价为元，由题意得：，

解得：，

经检验：是原方程的解；答（略）

（2）设购进甲种水果m千克，则乙种水果千克，利润为y元，由题意知：

，

∵甲种水果的重量不低于乙种水果重量的2倍，

∴，解得：，

∵-1<0，则y随m的增大而减小，

∴当m=100时，y最大，且为-100+1650=1550元，

∴购进甲种水果100千克，则乙种水果50千克，获得最大利润1550元.

26.（本题满分10分）

解：（1）①∵AD=CD=DE，∴∠DEA=∠DAE，

在正方形ABCD中，∠ADC=90°，∠CDE=α，∴∠ADE=90°+α，

∴，

②△AEF是等腰直角三角形，理由如下

∵CD=DE，∠CDE=α，∴，

∵，∴，

又∵DF⊥AE，AD=DE∴DF垂直平分AE∴FA=FE，

∴∠EAF=∠AEF=45°，∴∠AFE=90°，∴△AEF是等腰直角三角形；

（2）连接AC，∵EH⊥CD∴∠EHD=∠EHC=90°，

∵四边形ABCD是正方形，∴，∠ABC=90°，

∴，在Rt△ABC中，，

在Rt△AFC中，∠AFC=90°，，

∴，∴，

在Rt△EHD和Rt△EHC中，，

设，则，∴，

解得：，∴.

27.（本题满分10分）

解：（1）如图，延长EA交x轴于点G，过点F作x轴的垂线，垂足分别为H

∵四边形ABCD是菱形∴CD=AD=AB，CD∥AB

∵AB∥x轴，AE⊥CD∴EG⊥x轴，∠D+∠DAE=90°

∵OA⊥AD∴∠DAE+∠GAO=90°∴∠GAO=∠D

∵OA=OD∴△DEA≌△AGO（AAS）∴DE=AG，AE=OG

设CE=a，则，

在Rt△AED中，由勾股定理得：

∴，

∴，

∵AB∥x轴，AG⊥x轴，FH⊥x轴

∴四边形是矩形∴，

∵E点在双曲线上∴即

∵F点在双曲线上，且F点的纵坐标为4a

∴即∴∴

（2）∵

∴由（1）得

解得：∴∴

28.（本题满分10分）

（1），

（2）∵∠C=90°，∠A=30°，BC=2，∴，

∵D为AB中点，∴，

∵ADEP是平行四边形，∴AD//PE，AD=PE，

∵△APD沿PD翻折得到△EPD，∴AP=PE，

∴，∴.

（3）存在，理由如下：

①当BD为边时，∵∠A=30°，∠ACB=90°，∴∠B=60°，

∵四边形DBCE是平行四边形，

∴CE=BD，CE//BD，DE//BC，

∴∠ECP=∠A=30°，∠CED=∠ADE=∠B=60°，

∵△APD沿PD翻折得到△EPD，

∴∠ADP=∠EDP=30°，AP=PE，

∴∠PAD=∠PDA=30°，∴AP=PD=PE，

∴∠PED=∠PDE=30°，∴∠PEC=∠PED+∠DEC=90°，

∵∠ECP=30°，∴PC=2PE，

∴，即解得：

②当BD为对角线时，∵BC=BD=AD，∠B=60°，

∴△BCD都是等边三角形，∴∠ACD=30°，

∵四边形BCDE是平行四边形，∴平行四边形BCDE为菱形，

∴，，

又∵CD=CD，∴△ACD≌△ECD，

∴AC=CE，∴△ECD是△ACD沿CD翻折得到，

∵△APD沿PD翻折得到△EPD，∴点P与点C重合，

∴

故当或时，以B、C、E、D为顶点的四边形是平行四边形.