浙江省宁波市区慈溪市2021-2022学年八年级下学期数学期末统考试题卷（无答案）

这是一份浙江省宁波市区慈溪市2021-2022学年八年级下学期数学期末统考试题卷（无答案），共4页。试卷主要包含了选择题，解答题（第 17等内容，欢迎下载使用。
慈溪市2021-2022学年八年级下学期数学期末统考试题一、选择题 (每小题 3 分, 共 30 分, 在每小题给出的四个选项中, 只有一项符合题目要求)1. 下列图形是用数学家名字命名的, 其中是中心对称图形的是(    )
A. 赵爽弦图  B. 笛卡尔心形线  C. 彭烈斯三角 D. 斐波那契螺旋线函数中, 自变量的取值范围是(    )
A.    B. 且   C.    D. 且
3. 在中, , 则的度数为(    )
A.      B.       C.       D. 4.反比例函数为常数的图象经过点, 则它的图象还经过点(    )
A.     B.     C.     D. 5.下列一元二次方程中, 没有实数根的是(    )
A.         B.
C.             D. 6.有15名学生参加学校举办的“最强大脑”智力竞赛，比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差，若去掉一个最高分，一个最低分，则一定不会发生变化的统计量是(    )A. 众数       B. 平均数       C. 位位敪     D. 方差
7. 如图, 已知, 下列鸰述不正确的是(    )
A. 当时, 它是菱形
B. 当 时, 它是菱形
C. 当时, 它是矩形
D. 当时, 它是正方形
8. 用反证法证明命题: “在直角三角形中, 至少有一个锐角不大于 ”, 应假设(    )
A. 没有一个锐角不大于           B. 至多有一个锐角大于
C. 两个锐角都不大于             D. 两个锐角都小于
9. 一个同学经过培训后会做某项实验, 回到班级后他先教会了名同学, 然后这 名同学每人又教会了名同学, 这时恰好全班36人都会做这项实验了，根据以上情景, 可列方程为(    )
A.                 B.                    D.
10. 如图, 正方形中, 点为延长线上任一点, 连结, 过点作, 交的延长线于点, 过点作于点. 下列结论: (1) (2) ;(3) ; (4)若, 则.
其中正确的个数为(    )
A. 1       B. 2      C. 3         D. 4
二、填空题（每小题 4 分, 共 24 分)
11. 计算: _________.
12. 甲、乙两支仪仗队的队员人数相同, 平均身高相同, 身高的方差分别为甲 米 则甲、乙两支仪仗队的队员身高较整齐的是_________队. (填 “甲” 或 “乙”)
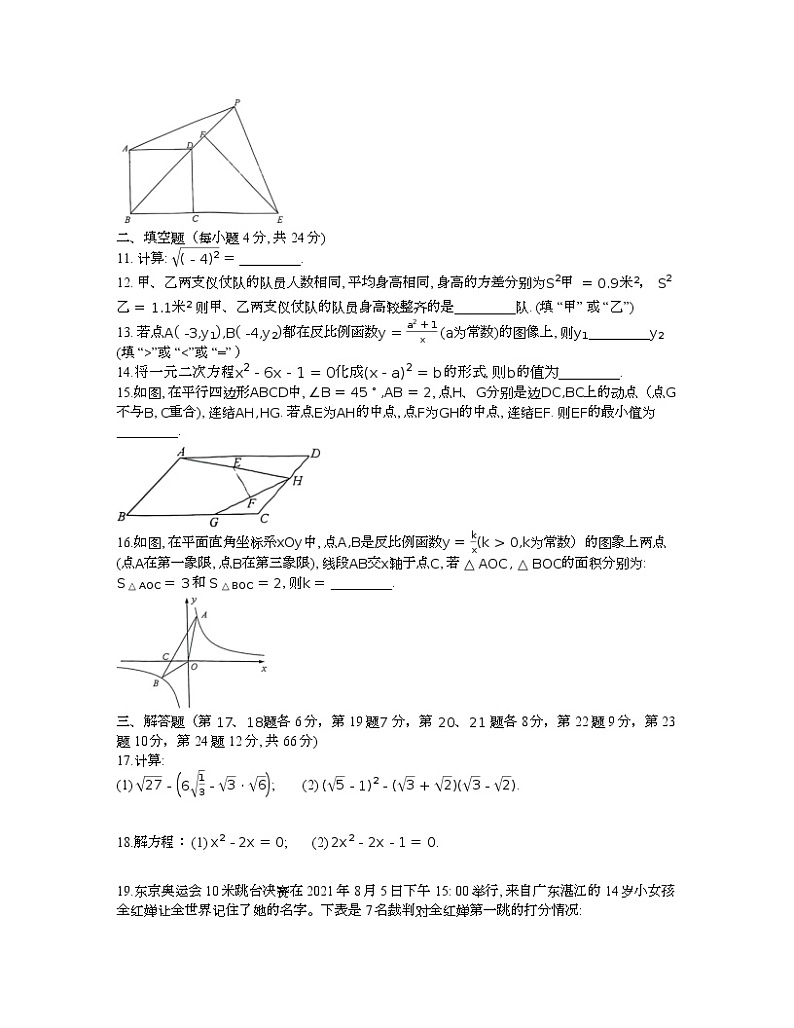
13. 若点都在反比例函数 (为常数)的图像上, 则_________ (填 “>”或 “<”或 “=” ）14.将一元二次方程化成的形式, 则的值为_________.15.如图, 在中, , 点分别是边上的动点（点不与, 重合), 连结. 若点为的中点, 点为的中点, 连结. 则的最小值为_________.16.如图, 在平面直角坐标系中, 点是反比例函数为常数）的图象上两点 (点在第一象限, 点在第三象限), 线段交轴于点, 若的面积分别为: 和 , 则_________.
三、解答题（第 题各 6 分，第 19 题题各8分，第22题9分，第23题10分，第 24 题 12 分, 共 66 分)17.计算:
(1) ;        (2) .  18.解方程： (1) ;       (2) .  19.东京奥运会10米跳台决赛在2021年8月5 日下午15: 00举行, 来自广东湛江的 14岁小女孩全红婵让全世界记住了她的名字。下表是7名裁判对全红婵第一跳的打分情况:难度系数裁判打分 (分)10 (1)  写出7名裁判打分的众数和中位数.
(2) 跳水比赛计分规则规定, 在7个得分中去掉1个最高分和剩下5个得分的平均值为这一跳的完成分, 根据 “最后得分=难度系数 完成分 ”, 那么全红婵第一跳的最后得分多少?  20.并利用网格仅用无刻度的直尺完成作图, 作图要求保留痕迹, 不写作法.
(1) 如图1 , 点均为格点, 请在图中画出，并标出该平行四边形的对城中心O.
(2)如图2，在平行四边形中, 点分别在边, 且格点，在小正方形内部, 连结, 请先判断四边形的形状, 然后作出的平分线.  21.如图, 已知反比例函数为常数的图象交于两点.
(1) 求反比例函数及一次函数的表达式;
(2) 已知点, 过点作平行于轴的直线, 交一次函数图像于点且点在第一象限内，交反比例函数图象于点. 若点到点的距离小于线段结合函数图象直接写出n的取值范围.  22.如图, 在矩形中, , 把边沿对角线平移, 移动后的点分别对应点, 连结.
(1) 求证: 四边形是平行四边形;
(2) 当平行四边形为菱形时, 求边平移的距离.  23.如图, 一条笔直的竹竿斜靠在一道垂直于地面的增面上, 一端在墙面处, 另一端在地处, 墙角记为点.
(1) 若 米, 米.
   1)竹竿的顶端沿墙下滑1米, 那么点将向外移动多少米?
   2)竹竿的顶端从处沿墙下滑的距离与点如果不可能，请说明理由; 如果可能, 请求出移动的距离 (保留根号).
(2) 若, 则顶端下滑的距离与底端请说明理由: 若不等, 请比较顶端下滑的距离与底端外移的距离的大小.  24.如图, 在 中, 于点, 点在线段上, 过点作 于点于点, 线段与线段交于点.
(1) , 求的度数.
(2) . 求证: .
(3) 在(2)的条件下，解答下列问题:
   1)已知, 求的面积.
   2)用等式表示线段的数量关系，并给出证明.