广东省惠州市惠城区2021-2022学年八年级下学期期末考试模拟训练卷（含答案）

这是一份广东省惠州市惠城区2021-2022学年八年级下学期期末考试模拟训练卷（含答案），共17页。试卷主要包含了下列运算正确的是，在平面直角坐标系中，点P等内容，欢迎下载使用。

广东省惠州市惠城区2022年八年级下册期末考试模拟训练卷
满分120分 时间90分钟
一．选择题（共10小题，满分30分，每小题3分）
1．若在实数范围内有意义，则a的取值范围是（　　）
A．a＞﹣2 B．a＜﹣2 C．a≥﹣2 D．a≤﹣2
2．以下列各组数据为边，不能组成直角三角形的是（　　）
A．1.5，2，2.5 B．，， C．30，40，50 D．1，2，
3．某班为了解学生每周“家务劳动”情况，随机调查了7名学生每周的劳动时间，一周内累计参加家务劳动的时间分别为：2小时、3小时、2小时、3小时、2.5小时、3小时、1.5小时，则这组数据的中位数为（　　）
A．1.5小时 B．2小时 C．2.5小时 D．3小时
4．已知三角形的周长是16，它的三条中位线围成的三角形的周长是（　　）
A．16 B．12 C．8 D．4
5．如图，四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（　　）

A．∠ABD＝∠BDC，OA＝OC B．∠ABC＝∠ADC，AB＝CD
C．∠ABC＝∠ADC，AD∥BC D．∠ABD＝∠BDC，∠BAD＝∠DCB
6．下列运算正确的是（　　）
A． B． C． D．
7．一次函数y＝﹣2x+1的图象大致是（　　）
A．B．C．D．
8．在平面直角坐标系中，点P（x，4）到原点O的距离等于5，则x的值是（　　）
A．±3 B． C．﹣3 D．3
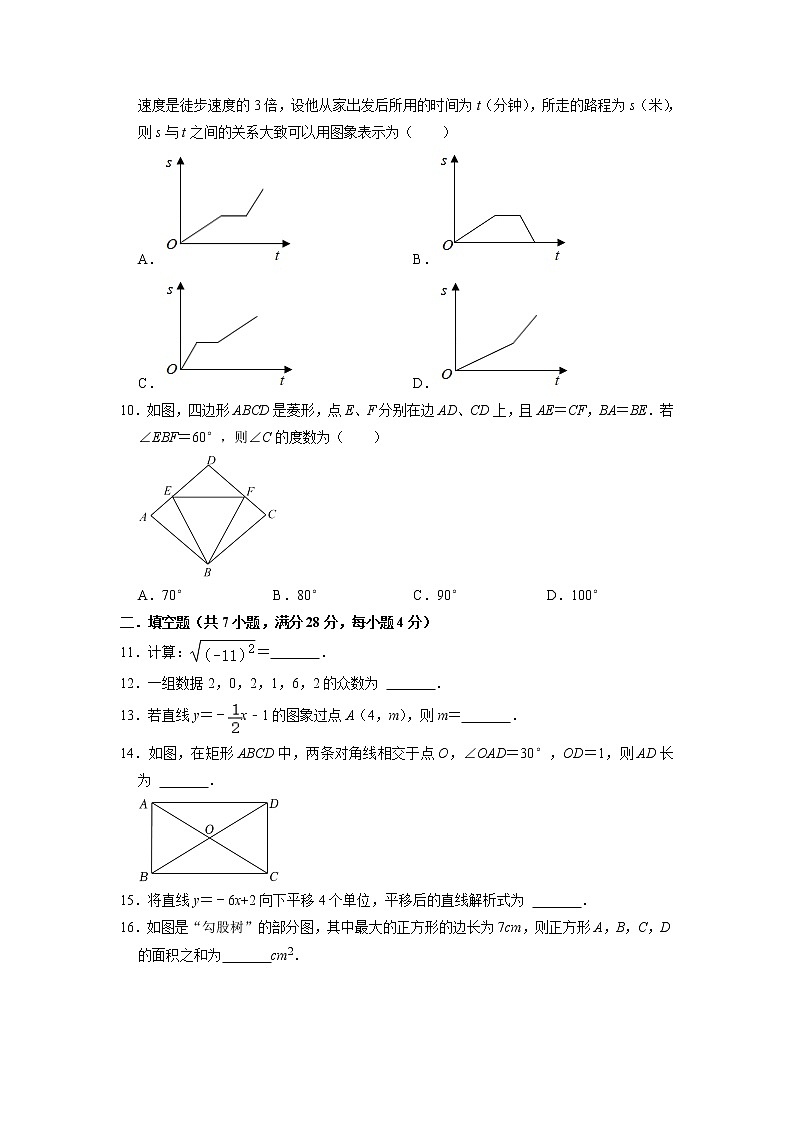
9．小刚从家出发徒步到同学家取自行车，在同学家逗留几分钟后他骑车原路返回，他骑车速度是徒步速度的3倍，设他从家出发后所用的时间为t（分钟），所走的路程为s（米），则s与t之间的关系大致可以用图象表示为（　　）
A． B．
C． D．
10．如图，四边形ABCD是菱形，点E、F分别在边AD、CD上，且AE＝CF，BA＝BE．若∠EBF＝60°，则∠C的度数为（　　）

A．70° B．80° C．90° D．100°
二．填空题（共7小题，满分28分，每小题4分）
11．计算：＝　 　．
12．一组数据2，0，2，1，6，2的众数为 　 　．
13．若直线y＝﹣x﹣1的图象过点A（4，m），则m＝　 　．
14．如图，在矩形ABCD中，两条对角线相交于点O，∠OAD＝30°，OD＝1，则AD长为 　 　．

15．将直线y＝﹣6x+2向下平移4个单位，平移后的直线解析式为 　 　．
16．如图是“勾股树”的部分图，其中最大的正方形的边长为7cm，则正方形A，B，C，D的面积之和为　 　cm2．

17．如图，已知菱形ABCD中，∠ABC＝60°，AB＝8，过线段BD上的一个动点P（不与B、D 重合）分别向直线AB、AD作垂线，垂足分别为E、F．
（1）BD的长是　 　；
（2）连接PC，当PE+PF+PC取得最小值时，此时PB的长是　 　．

三．解答题（共8小题，满分62分）
18．（6分）计算：．



19．（6分）四边形ABCD中，AD＝BC，BE＝DF，AE⊥BD，CF⊥BD，垂足分别为E、F．求证：四边形ABCD是平行四边形．



20．（6分）如图，小旭放风筝时，风筝线断了，风筝挂在了树上．他想知道风筝距地面的高度．于是他先拉住风筝线垂直到地面上，发现风筝线多出1米，然后把风筝线沿直线向后拉开5米，发现风筝线末端刚好接触地面（如图为示意图）．请你帮小旭求出风筝距离地面的高度AB．



21．（8分）21世纪已经进入了中国太空时代，2021年到2022年，我国会通过11次航天发射完成空间站建设，空间站由“天和”核心舱、“问天”和“梦天”两个实验舱，我国空间站的建成将为开展太空实验及更广泛的国际合作提供精彩舞台．校团委以此为契机，组织了“中国梦•航天情”系列活动．下面是八年级甲，乙两个班各项目的成绩（单位：分）：
（1）如果根据三项成绩的平均分计算最后成绩，请通过计算说明甲、乙两班谁将获胜；
（2）如果将知识竞赛、演讲比赛、版面创作按5：3：2的比例确定最后成绩，请通过计算说明甲乙两班谁将获胜．
项目班次
知识竞赛
演讲比赛
版面创作
甲
85
91
88
乙
90
84
87

22．（8分）某地实验中学为活跃班级体育大课间，计划分两次购进一批羽毛球和乒乓球．第一次分别购进羽毛球和乒乓球20盒和15盒，共花费475元；第二次分别购进羽毛球和乒乓球10盒和5盒，共花费225元．若两次购进的羽毛球和乒乓球的价格均分别相同．
（1）羽毛球和乒乓球每盒的价格分别是多少元？
（2）若购买羽毛球和乒乓球共30盒，且乒乓球的数量少于羽毛球数量的3倍，请你给出一种费用最省的方案，并求出该方案所需费用．



23．（8分）如图，在正方形ABCD中，点E为线段BC上一动点（点E不与点B、C重合），点B关于直线AE的对称点为F，作射线EF交CD于H，连接AF．
（1）求证：AF⊥EH；
（2）连接AH，小王通过观察、实验，提出猜想：点E在运动过程中，∠EAH的度数始终保持不变．你帮助小王求出∠EAH的度数．



24．（10分）如图，一次函数y＝x+3的图象l1与x轴相交于点B，与过点A（3，0）的一次函数的图象l2相交于点C（1，m）．
（1）求一次函数图象l2相应的函数表达式；
（2）求△ABC的面积．



25．（10分）（一）阅读下面内容：
＝＝；
＝＝﹣；
＝＝﹣2．
（二）计算：
（1）；
（2）（n为正整数）．
（3）+++…+．























广东省惠州市惠城区2022年八年级下册期末考试模拟训练卷
参考答案
一．选择题（共10小题，满分30分，每小题3分）
1．若在实数范围内有意义，则a的取值范围是（　　）
A．a＞﹣2 B．a＜﹣2 C．a≥﹣2 D．a≤﹣2
【解答】解：∵在实数范围内有意义，
∴2+a≥0，
解得：a≥﹣2．
故选：C．
2．以下列各组数据为边，不能组成直角三角形的是（　　）
A．1.5，2，2.5 B．，， C．30，40，50 D．1，2，
【解答】解：A、1.52+22＝2.52，是直角三角形，不符合题意；
B、（）2+（）2≠（）2，不是直角三角形，符合题意；
C、302+402＝502，是直角三角形，不符合题意；
D、12+（）2＝22，是直角三角形，不符合题意．
故选：B．
3．某班为了解学生每周“家务劳动”情况，随机调查了7名学生每周的劳动时间，一周内累计参加家务劳动的时间分别为：2小时、3小时、2小时、3小时、2.5小时、3小时、1.5小时，则这组数据的中位数为（　　）
A．1.5小时 B．2小时 C．2.5小时 D．3小时
【解答】解：把这些数据从小到大排列为1.5小时、2小时、2小时、2.5小时、3小时、3小时、3小时，排在最中间的数是2.5小时，
故选：C．
4．已知三角形的周长是16，它的三条中位线围成的三角形的周长是（　　）
A．16 B．12 C．8 D．4
【解答】解：∵三角形的周长是16，
∴它的三条中位线围成的三角形的周长是16×＝8．
故选：C．
5．如图，四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（　　）

A．∠ABD＝∠BDC，OA＝OC B．∠ABC＝∠ADC，AB＝CD
C．∠ABC＝∠ADC，AD∥BC D．∠ABD＝∠BDC，∠BAD＝∠DCB
【解答】解：A、∵∠ABD＝∠BDC，OA＝OC，
又∠AOB＝∠COD，
∴△AOB≌△COD，
∴DO＝BO，
∴四边形ABCD是平行四边形，故此选项不合题意；
B、∠ABC＝∠ADC，AB＝CD不能判断四边形ABCD是平行四边形，故此选项符合题意；
C、∵AD∥BC，
∴∠ABC+∠BAD＝180°，
∵∠ABC＝∠ADC，
∴∠ADC+∠BAD＝180°，
∴AB∥CD，
∴四边形ABCD是平行四边形，故此选项不合题意；
D、∵∠ABD＝∠BDC，∠BAD＝∠DCB，
∴∠ADB＝∠CBD，
∴AD∥CB，
∵∠ABD＝∠BDC，
∴AB∥CD，
∴四边形ABCD是平行四边形，故此选项不合题意；
故选：B．

6．下列运算正确的是（　　）
A． B． C． D．
【解答】解：A、与不是同类二次根式，不能合并计算，故此选项不符合题意；
B、5+，故此选项不符合题意；
C、与不是同类二次根式，不能合并计算，故此选项不符合题意；
D、2﹣，正确，故此选项符合题意；
故选：D．
7．一次函数y＝﹣2x+1的图象大致是（　　）
A． B．
C． D．
【解答】解：∵k＝﹣2＜0，b＝1＞0，
∴一次函数y＝2x+1的图象经过一、二、四象限．
故选：C．
8．在平面直角坐标系中，点P（x，4）到原点O的距离等于5，则x的值是（　　）
A．±3 B． C．﹣3 D．3
【解答】解：∵点P（x，4）到原点O的距离等于5，
∴x2+42＝52，
解得：x＝±3，
故选：A．
9．小刚从家出发徒步到同学家取自行车，在同学家逗留几分钟后他骑车原路返回，他骑车速度是徒步速度的3倍，设他从家出发后所用的时间为t（分钟），所走的路程为s（米），则s与t之间的关系大致可以用图象表示为（　　）
A． B．
C． D．
【解答】解：小刚取车的整个过程共分三个阶段：
①徒步从家到同学家，s随时间t的增大而增大；
②在同学家逗留期间，s不变；
③骑车返回途中，速度是徒步速度的3倍，s随t的增大而增大，并且比徒步时的直线更陡；
纵观各选项，只有A选项符合．
故选：A．
10．如图，四边形ABCD是菱形，点E、F分别在边AD、CD上，且AE＝CF，BA＝BE．若∠EBF＝60°，则∠C的度数为（　　）

A．70° B．80° C．90° D．100°
【解答】解：∵四边形ABCD是菱形，
∴AB＝BC，∠A＝∠C，
在△ABE与△CBF中，
，
∴△ABE≌△CBF（SAS），
∴∠ABE＝∠CBF，BE＝BF，
∴BC＝BF，
∴∠C＝∠BFC，
设∠ABE＝∠CBF＝α，
∵∠EBF＝60°，
∴∠ABC＝2α+60°，
∴∠C＝180°﹣∠ABC＝180°﹣2α﹣60°＝120°﹣2α，
∴∠BFC＝∠C＝120°﹣2α，
∵∠C+∠BFC+∠CBF＝180°，
∴120°﹣2α+120°﹣2α+α＝180°，
∴α＝20°，
∴∠C＝80°，
故选：B．
二．填空题（共7小题，满分28分，每小题4分）
11．计算：＝　11　．
【解答】解：＝＝11．
故答案为：11．
12．一组数据2，0，2，1，6，2的众数为 　2　．
【解答】解：这组数据中数据2出现3次，次数最多，
所以这组数据的众数为2，
故答案为：2．
13．若直线y＝﹣x﹣1的图象过点A（4，m），则m＝　﹣3　．
【解答】解：∵直线y＝﹣x﹣1的图象过点A（4，m），
∴m＝﹣×4﹣1＝﹣3．
故答案为：﹣3．
14．如图，在矩形ABCD中，两条对角线相交于点O，∠OAD＝30°，OD＝1，则AD长为 　　．

【解答】解：∵四边形ABCD为矩形，
∴∠BAD＝90°，AO＝OD＝OC＝OB＝1，
∴∠OAD＝∠ODA＝30°，BD＝2OD＝2，
∴∠AOB＝60°，
∴△AOB为等边三角形；
∴AB＝OA＝1，
∴AD＝＝＝．
故答案为：．
15．将直线y＝﹣6x+2向下平移4个单位，平移后的直线解析式为 　y＝﹣6x﹣2　．
【解答】解：将直线y＝﹣6x+2向下平移4个单位，平移后的直线解析式为y＝﹣6x+2﹣4＝﹣6x﹣2，
故答案为：y＝﹣6x﹣2．
16．如图是“勾股树”的部分图，其中最大的正方形的边长为7cm，则正方形A，B，C，D的面积之和为　 　49　cm2．

【解答】解：如图，

∵所有的三角形都是直角三角形，所有的四边形都是正方形，
∴正方形A的面积＝a2，正方形B的面积＝b2，
正方形C的面积＝c2，正方形D的面积＝d2，
又∵a2+b2＝x2，c2+d2＝y2，
∴正方形A、B、C、D的面积和＝（a2+b2）+（c2+d2）＝x2+y2＝72＝49cm2．
故答案为：49．
17．如图，已知菱形ABCD中，∠ABC＝60°，AB＝8，过线段BD上的一个动点P（不与B、D 重合）分别向直线AB、AD作垂线，垂足分别为E、F．
（1）BD的长是　8　；
（2）连接PC，当PE+PF+PC取得最小值时，此时PB的长是　　．

【解答】解：（1）连接AC，交BD与点O，

∵四边形ABCD是菱形，∠ABC＝60°，
∴△ABC为等边三角形，AC＝AB＝8，
根据菱形性质得：AO＝CO＝AC＝4，OB＝OD，AC⊥BD，
根据勾股定理得：BD＝2OB＝2×＝8；

（2）延长FP交BC于点M，则FM⊥BC．

∵PM＝PE，
∴PE+PF＝PF+PM＝FM，
又∵S菱形ABCD＝AC•BD＝BC•FM，
∴×8×8＝8•FM，即FM＝4，
∴要使PE+PF+PC取最小值，只要PC取最小值．
当CP⊥BD，即点P与点O重合时，PE+PF+PC的值最小．
此时PB＝BO＝DO＝BD＝4．
故答案为：8；4．
三．解答题（共8小题，满分62分）
18．（6分）计算：．
【解答】解：
＝3﹣2+1﹣（2﹣1）
＝3﹣2+1﹣1
＝3﹣2．
19．（6分）四边形ABCD中，AD＝BC，BE＝DF，AE⊥BD，CF⊥BD，垂足分别为E、F．求证：四边形ABCD是平行四边形．

【解答】证明：∵BE＝DF，
∴BE﹣EF＝DF﹣EF，
即BF＝DE，
∵AE⊥BD，CF⊥BD，
∴∠AED＝∠CFB＝90°，
在Rt△ADE与Rt△CBF中，
，
∴Rt△ADE≌Rt△CBF（HL），
∴∠ADE＝∠CBF，
∴AD∥BC，
又∵AD＝BC，
∴四边形ABCD是平行四边形．
20．（6分）如图，小旭放风筝时，风筝线断了，风筝挂在了树上．他想知道风筝距地面的高度．于是他先拉住风筝线垂直到地面上，发现风筝线多出1米，然后把风筝线沿直线向后拉开5米，发现风筝线末端刚好接触地面（如图为示意图）．请你帮小旭求出风筝距离地面的高度AB．

【解答】解：设AB＝x，则AC＝x+1，
由图可得，∠ABC＝90°，BC＝5，
∴Rt△ABC中，AB2+BC2＝AC2，
即x2+52＝（x+1）2，
解得x＝12，
答：风筝距离地面的高度AB为12米．
21．（8分）21世纪已经进入了中国太空时代，2021年到2022年，我国会通过11次航天发射完成空间站建设，空间站由“天和”核心舱、“问天”和“梦天”两个实验舱，我国空间站的建成将为开展太空实验及更广泛的国际合作提供精彩舞台．校团委以此为契机，组织了“中国梦•航天情”系列活动．下面是八年级甲，乙两个班各项目的成绩（单位：分）：
（1）如果根据三项成绩的平均分计算最后成绩，请通过计算说明甲、乙两班谁将获胜；
（2）如果将知识竞赛、演讲比赛、版面创作按5：3：2的比例确定最后成绩，请通过计算说明甲乙两班谁将获胜．
项目班次
知识竞赛
演讲比赛
版面创作
甲
85
91
88
乙
90
84
87
【解答】解：（1）甲班的平均分为：（85+91+88）÷3＝88（分），
乙班的平均分为：（90+84+87）÷3＝87（分），
∵88＞87，
∴甲班将获胜；
（2）由题意可得，
甲班的平均分为：＝87.4（分），
乙班的平均分为：＝87.6（分），
∵87.4＜87.6，
∴乙班将获胜．
22．（8分）某地实验中学为活跃班级体育大课间，计划分两次购进一批羽毛球和乒乓球．第一次分别购进羽毛球和乒乓球20盒和15盒，共花费475元；第二次分别购进羽毛球和乒乓球10盒和5盒，共花费225元．若两次购进的羽毛球和乒乓球的价格均分别相同．
（1）羽毛球和乒乓球每盒的价格分别是多少元？
（2）若购买羽毛球和乒乓球共30盒，且乒乓球的数量少于羽毛球数量的3倍，请你给出一种费用最省的方案，并求出该方案所需费用．
【解答】解：（1）设羽毛球每盒的价格是x元，乒乓球每盒的价格是y元，
依题意得：，
解得：．
答：羽毛球每盒的价格是20元，乒乓球每盒的价格是5元．
（2）设购买羽毛球m盒，则购买乒乓球（30﹣m）盒，
依题意得：30﹣m＜3m，
解得：m＞．
设购买羽毛球和乒乓球共30盒所需费用为w元，则w＝20m+5（30﹣m）＝15m+150，
∵15＞0，
∴w随m的增大而增大，
∴当m＝8时，w取得最小值，最小值＝15×8+150＝270，此时30﹣m＝12．
答：当购买羽毛球8盒，乒乓球12盒时费用最低，最低费用为270元．
23．（8分）如图，在正方形ABCD中，点E为线段BC上一动点（点E不与点B、C重合），点B关于直线AE的对称点为F，作射线EF交CD于H，连接AF．
（1）求证：AF⊥EH；
（2）连接AH，小王通过观察、实验，提出猜想：点E在运动过程中，∠EAH的度数始终保持不变．你帮助小王求出∠EAH的度数．

【解答】解：（1）证明：∵点B关于直线AE的对称点为F，
∴AB＝AF，BE＝EF，
又∵AE＝AE，
∴△ABE≌△AFE（SSS），
∴∠AFE＝∠B＝90°，
∴AF⊥EH；
（2）连接AH，如图：

由（1）得AB＝AF，AF⊥EH，
∴AF＝AD，∠D＝∠AFH＝90°，AH＝AH，
∴△AFH≌△ADH（HL），
∴∠FAH＝∠DAH，
又∵∠BAE＝∠FAE，在正方形ABCD中，∠BAD＝90°，
∴∠EAH＝45°．
24．（10分）如图，一次函数y＝x+3的图象l1与x轴相交于点B，与过点A（3，0）的一次函数的图象l2相交于点C（1，m）．
（1）求一次函数图象l2相应的函数表达式；
（2）求△ABC的面积．

【解答】解：（1）∵点C（1，m）在一次函数y＝x+3的图象上，
∴m＝1+3＝4，
∴点C（1，4），
设一次函数图象l2相应的函数表达式为y＝kx+b，
把点A（3，0），C（1，4）代入得，
解得，
∴一次函数图象l2相应的函数表达式y＝﹣2x+6；
（2）∵一次函数y＝x+3的图象l1与x轴交于点B，
∴当y＝0时，0＝x+3，解得x＝﹣3，
∴B（﹣3，0），
∵A（3，0），C（1，4），
∴AB＝6，
∴S△ABC＝×6×4＝12．
25．（10分）（一）阅读下面内容：
＝＝；
＝＝﹣；
＝＝﹣2．
（二）计算：
（1）；
（2）（n为正整数）．
（3）+++…+．
【解答】解：（二）（1）原式＝﹣；
（2）﹣；
（3）原式＝﹣1+﹣+﹣+…+﹣+﹣＝﹣1＝9．