2022年初升高数学衔接讲义(第2套) 第9讲 二次函数与一元二次方程、不等式（教师版+学生版）

这是一份2022年初升高数学衔接讲义(第2套) 第9讲 二次函数与一元二次方程、不等式（教师版+学生版），文件包含2022年初升高数学衔接讲义第2套第9讲二次函数与一元二次方程不等式教师版含解析docx、2022年初升高数学衔接讲义第2套第9讲二次函数与一元二次方程不等式学生版docx等2份学案配套教学资源，其中学案共18页， 欢迎下载使用。
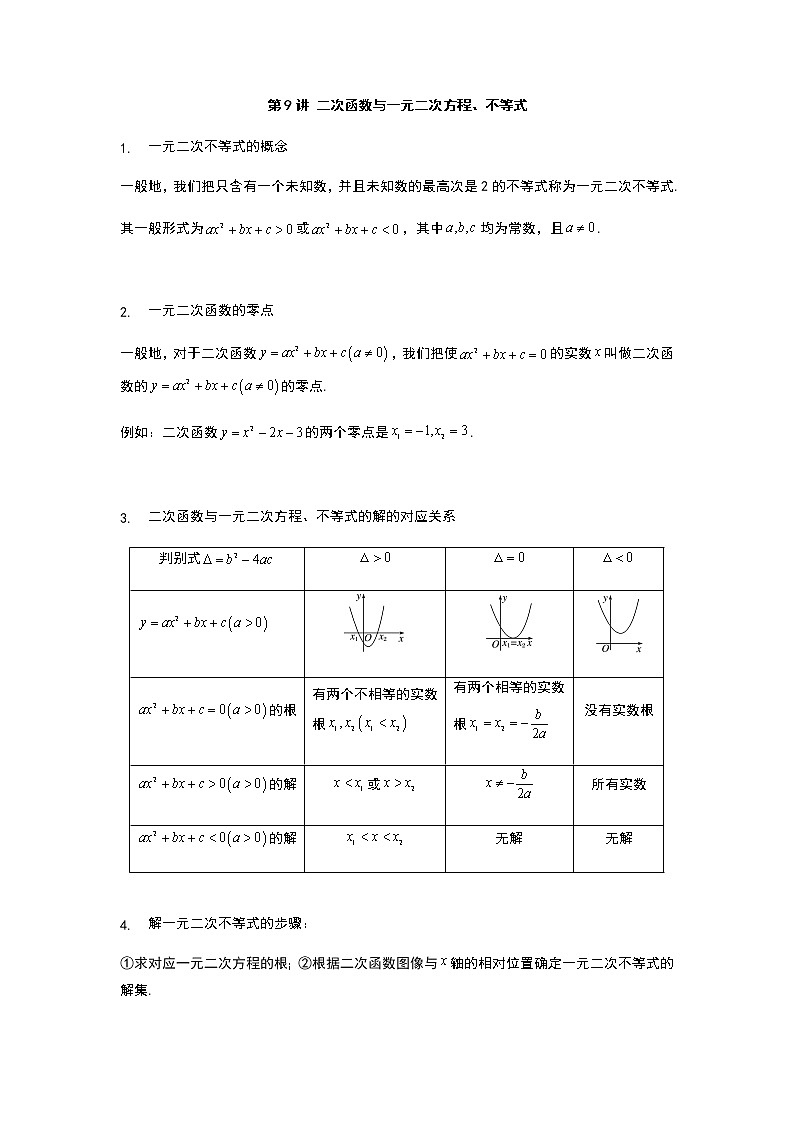
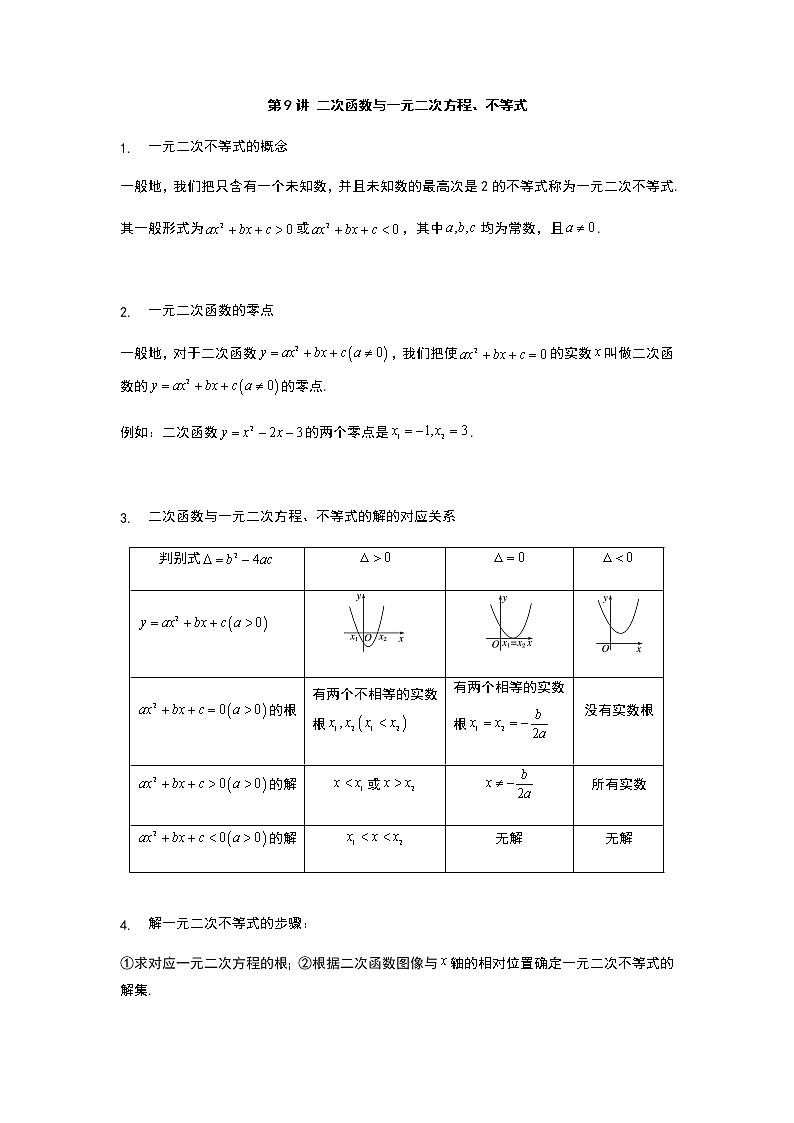
第9讲 二次函数与一元二次方程、不等式    一元二次不等式的概念一般地，我们把只含有一个未知数，并且未知数的最高次是2的不等式称为一元二次不等式.其一般形式为或，其中均为常数，且.     一元二次函数的零点一般地，对于二次函数，我们把使的实数叫做二次函数的的零点.例如：二次函数的两个零点是.     二次函数与一元二次方程、不等式的解的对应关系判别式的根有两个不相等的实数根有两个相等的实数根没有实数根的解或所有实数的解无解无解     解一元二次不等式的步骤：①求对应一元二次方程的根；②根据二次函数图像与轴的相对位置确定一元二次不等式的解集.示意图如下：                     分式不等式的解法：将分式不等式转化为整式不等式，然后再求解！  例1.解下列二次不等式(1)；          (2) ；             (3)【答案】(1)；(2)无解；(3) 例2.应满足什么条件才能使有意义？【答案】【解析】要使有意义，则，解得. 例3.若，解关于的不等式.【答案】见解析【解析】由得，当，即时，解得；当，即时，解得；当，即时，解得. 例4.解下列分式不等式（1）；               (2)；                   (3)  【答案】(1)；(2)；(3).【解析】(1)，，解得；（2），，，，解得；（3），可化为，，解得. 例5.已知二次函数，令，解得.（1）求二次函数的解析式；（2）当关于的不等式恒成立时，求实数的范围.【答案】(1)；(2).【解析】(1)由解得，所以，解得，所以解析式为；(2)由得恒成立，则，解得，所以实数的范围为.  例6. (1)    方程有一个正根和一个负根，求实数的取值范围；(2)    方程有一个根大于1，一个根小于1，求实数的取值范围；(3)    取何实数值时，关于的方程的两个不相等的实根都大于2？(4)    若关于的方程有两实根，且，，求实数的取值范围.【答案】(1)；(2)；(3)；(4).【解析】(1)解法一：令，依题意知或解得；解法二：依题意知，解得；(2)解法一：令，则，解得；解法二：依题意知，，解得；(3)解法一：令，依题意知，解得；解法二：依题意知，，解得；(4)设，依题意知，解得. 例7. (1)    若关于的不等式对任意的实数恒成立,求实数的取值范围；(2)    若不等式对任意实数恒成立，求实数的取值范围；(3)    当时，不等式恒成立，求实数的取值范围；(4)    已知函数，当时恒有，求实数的取值范围；(5)    已知函数，若对于恒成立，求实数的取值范围．【答案】(1)；(2)；(3)；(4)；(5).【解析】(1)当时，不等式化为，不符合题意；当时，要使对任意的实数恒成立，则，解得；(2)由得恒成立，则，解得；(3)设，依题意可知，解得；(4)由时恒有得，设，依题意可知或，解得或，综上所述，；(5)，设，，所以是关于的一次函数，依题意时恒成立，只需，解得.跟踪训练    解下列不等式：（1）；                       (2)；(3) ；                     (4)；(5)；                             (6)；(7)；               (8)【答案】(1)；(2)；(3)；(4)；(5)；(6)；(7)；(8).     二次方程的两根为，若，则不等式的解为          .【答案】     已知，则关于的不等式的解是(    ) A.或      B.或        C.       D.【答案】A【解析】，，由得，，，选A.     若关于的不等式的解中，恰有3个整数，则实数应满足(    ) A.            B.或         C.             D.或 【答案】D【解析】由得，当时，，依题意得；当时，，依题意得，综上所述，或，选D.      在上定义运算：，则满足的实数的取值范围是(    ) A.       B.        C.或          D.【答案】B【解析】依题意得，解得，选B.     若不等式恒成立，则实数的取值范围是          .【答案】【解析】由得恒成立，，恒成立，只需，解得，所以的取值范围是.     若不等式恒成立，则实数的取值范围是          .【答案】【解析】由得恒成立，当，即时，不等式化为恒成立，符合题意；当，即时，依题意得，解得，综上所述，的取值范围是.     若不等式对任意的实数均成立，则实数的取值范围是          .【答案】【解析】当时，不等式化为恒成立，符合题意；当时，则，解得，综上所述，的取值范围是.     当时，方程有两个不相等的实根，求实数的取值范围.【答案】【解析】依题意方程有两个不相等的实根，设，则，解得，所以的取值范围为.