(辅导班专用)人教版数学九年级暑假讲义+课堂小测(提高班)09《旋转》（2份打包，教师版+学生版）

这是一份(辅导班专用)人教版数学九年级暑假讲义+课堂小测(提高班)09《旋转》（2份打包，教师版+学生版），文件包含辅导班专用人教版数学九年级暑假讲义+课堂小测提高班09《旋转》教师版docx、辅导班专用人教版数学九年级暑假讲义+课堂小测提高班09《旋转》学生版docx等2份试卷配套教学资源，其中试卷共49页， 欢迎下载使用。
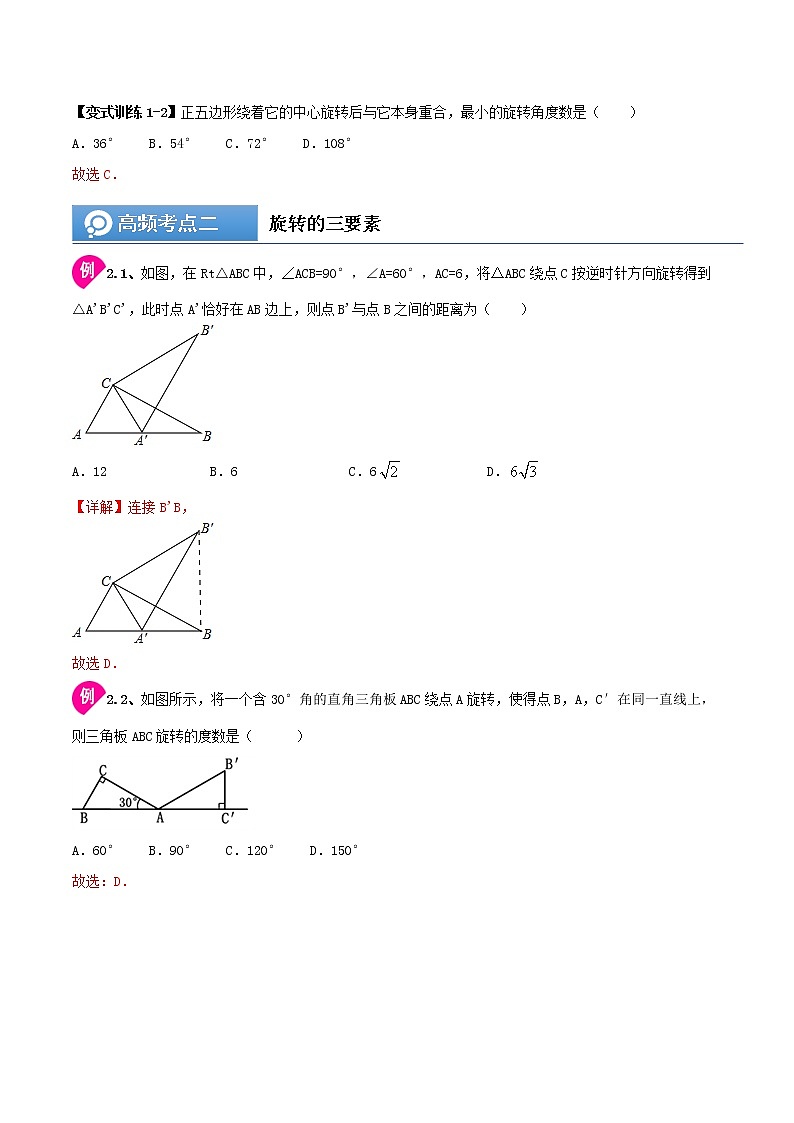
第09讲 （一）旋转的性质如图，将△ABC绕点A逆时针旋转一定的角度，得到△ADE，且AD⊥BC.若∠CAE＝65°，∠E＝60°，则∠BAC的大小为(　　)A.60° B.75° C.85° D.95°知识点一 旋转的基础旋转的概念：把一个平面图形绕着平面内某一点转动一个角度，叫作图形的旋转.点叫作旋转中心，转动的角叫作旋转角.如图形上的点经过旋转变化点，那么这两个点叫作这个旋转的对应点.如图所示，是绕定点逆时针旋转得到的，其中点与点叫作对应点，线段与线段叫作对应线段，与叫作对应角，点叫作旋转中心，（或）的度数叫作旋转的角度.【注意】图形的旋转由旋转中心、旋转方向与旋转的角度所决定.知识点二 旋转的三要素【旋转的三要素】旋转中心、旋转方向和旋转角.知识点三：旋转作图旋转的特征：①对应点到旋转中心的距离相等；②对应点与旋转中心所连线段的夹角等于旋转角；③旋转前、后的图形全等.旋转作图的步骤：①确定旋转中心、旋转方向、旋转角；②找出图形上的关键点；③连接图形上的关键点与旋转中心，然后按旋转方向分别将它们旋转一定的角度，得到关键点的对应点；④按原图的顺序连接这些对应点，即得旋转后的图形.1.1、如图，把△AOB绕点O顺时针旋转得到△COD，则旋转角是（    ）A．∠AOC B．∠AOD C．∠AOB D．∠BOC1.2、如图,将△ABC绕着点C顺时针旋转50°后得到△A'B'C'.若∠A=40°，∠B'=110°，∠BCA'的度数是（　　）A.110° B.80° C.40° D.30°【变式训练1-1】如图，在中，，将在平面内绕点A旋转到的位置，使，则旋转角的度数为　　A．    B．    C．    D．【变式训练1-2】正五边形绕着它的中心旋转后与它本身重合，最小的旋转角度数是（　　）A．36°    B．54°    C．72°    D．108°   2.1、如图，在Rt△ABC中，∠ACB=90°，∠A=60°，AC=6，将△ABC绕点C按逆时针方向旋转得到△A'B'C'，此时点A'恰好在AB边上，则点B'与点B之间的距离为（　　）A．12 B．6 C．6 D．2.2、如图所示，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一直线上，则三角板ABC旋转的度数是（    　）A．60°    B．90°    C．120°    D．150°2.3、如图，将绕直角顶点顺时针旋转，得到，连接若，则的度数是(    )A． B． C． D．【变式训练2-1】如图，将△ABC绕点A顺时针旋转60°得到△ADE，点C的对应点E恰好落在BA的延长线上，DE与BC交于点F，连接BD．下列结论不一定正确的是（　　）A.AD=BD B.AC∥BD C.DF=EF D.∠CBD=∠E【变式训练2-2】如图，将△ABC绕点C顺时针旋转90°得到△EDC．若点A，D，E在同一条直线上，∠ACB=20°，则∠ADC的度数是　　A．55° B．60° C．65° D．70°【变式训练2-3】如图，已知四边形ABCD是边长为4的正方形，E为AB的中点，将△ADE绕点D沿逆时针方向旋转后得到△DCF，连接EF，则EF的长为（　　）A．2 B．2 C．2 D．23、如图，在方格纸中每个小正方形的边长均为个单位，的三个顶点都在小方格的顶点上。（1）在图中作出将向下平移个单位后的图形：（2）在图中作出以为旋转中心，沿顺时针方向旋转后的图形.    【变式训练3-1】在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,3),B(1,1),C(5,1).(1)把△ABC平移后,其中点A移到点A1(4,5),画出平移后得到的△A1B1C1;(2)把△A1B1C1绕点A1按逆时针方向旋转90°,画出旋转后的△A2B2C2. 4、如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连接CE绕点C顺时针旋转110°,得到线段CF,连接BE,DF,若∠E=86°,求∠F的度数.   【变式训练4-1】如图，D是等边三角形ABC内一点，将线段AD绕点A顺时针旋转60°，得到线段AE，连接CD，BE． （1）求证：∠AEB=∠ADC；（2）连接DE，若∠ADC=105°，求∠BED的度数． 1．如图，将矩形 ABCD 绕点 A 顺时针旋转到矩形 AB′C′D′的位置，旋转角为α(0°＜α＜90°)．若∠1＝112°，则∠α的大小是(    )A．68° B．20° C．28° D．22°2．如图，正方形OABC绕着点O逆时针旋转40°得到正方形ODEF，连接AF，则∠OFA的度数是（ ）.A．15° B．20° C．25° D．30°3．如图，将△ABC绕点A按逆时针方向旋转100°，得到△AB1C1，若点B1在线段BC的延长线上，则∠BB1C1的大小为（　　）A．70°    B．80°    C．84°    D．86°4.如图，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，连接AD．下列结论一定正确的是（　　）A．∠ABD＝∠E    B．∠CBE＝∠C    C．AD∥BC    D．AD＝BC5.如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是　　. 6.如图,在△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕点A顺时针旋转得到△ADE(其中点B恰好落在AC延长线上点D处,点C落在点E处),连接BD,则四边形AEDB的面积为　　. 7．如图，在矩形ABCD中，AD=3，将矩形ABCD绕点A逆时针旋转，得到矩形AEFG，点B的对应点E落在CD上，且DE=EF，则AB的长为_____．8．如图，在四边形ABCD中，AB=AD=4，∠A=60°，BC=4，CD=8．（1）求∠ADC的度数；（2）求四边形ABCD的面积．   9．如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）．（1）将△ABC向下平移5个单位后得到△A1B1C1，请画出△A1B1C1；（2）将△ABC绕原点O逆时针旋转90°后得到△A2B2C2，请画出△A2B2C2；（3）判断以O，A1，B为顶点的三角形的形状．（无须说明理由）10.四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．（1）求证：△ADE≌△ABF；（2）若BC=12，DE=5，求△AEF的面积．    1.如图，在正方形ABCD中，M为DC上一点，联结BM，将绕点C顺时针方向旋转得到联结如果，则的度数为　　A．          B．    C．          D．2.如图，将△OAB绕O点逆时针旋转60°得到△OCD，若OA＝4，∠AOB＝35°，则下列结论错误的是(　　)A．∠BDO＝60° B．∠BOC＝25° C．OC＝4 D．BD＝43．如图，△ABC中，AB＝4，AC＝3，BC＝2，将△ABC绕点A顺时针旋转60°得到△AED，则BE长为（　　）A.5 B.4 C.3 D.24．下列各图中，既可经过平移，又可经过旋转，由图形①得到图形②的是（　　）A．    B．    C．    D．5．如图，将△ABC绕着点C顺时针旋转50°后得到△A’B’C．若=40°，=110°，则∠的度数为（ ）A．30°    B．50°    C．80°    D．90°6．如图，△ABC中，∠ACB＝90°，∠ABC＝25°，以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，则旋转角的度数为（　　）A．65° B．60° C．50° D．40°7．如图，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，连接AD．下列结论一定正确的是（　　）A．∠ABD＝∠E    B．∠CBE＝∠C    C．AD∥BC    D．AD＝BC8．如图，在△ABC中，∠C＝90°，∠BAC＝70°，将△ABC绕点A顺时针旋转70°，B、C旋转后的对应点分别是B′和C′，连接BB′，则∠BB′C′的度数是（   ）A．35°    B．40°    C．45°    D．50°9.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=___.10．在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，请解答下列问题：（1）①作出△ABC向左平移4个单位长度后得到的△A1B1C1， 并写出点C1的坐标；②作出△ABC关于原点O对称的△A2B2C2， 并写出点C2的坐标；    （2）已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为（－4，－2），请直接写出直线l的函数解析式.          （二）中心对称如图，在平面直角坐标系中，点A，C在x轴上，点C的坐标为（﹣1，0），AC=2．将Rt△ABC先绕点C顺时针旋转90°，再向右平移3个单位长度，则变换后点A的对应点坐标是（　　）[来源:学.科.网]A.（2，2） B.（1，2） C.（﹣1，2） D.（2，﹣1）知识点一 中心对称与中心对称图形中心对称概念：把一个图形绕着某一点旋转，如图它能够与另一个图形重合，那么就说这两个U形关于这个点对称或中心对称，这个点叫作对称中心（简称中心）.这两个图形再旋转后能重合的对应点叫作关于对称中心的对称点.如图，绕着点旋转后，与完全重合，则称和关于点对称，点是点关于点的对称点.中心对称图形概念：把一个图形绕着某一个点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形叫作中心对称图形，这个点就是它的对称中心.中心对称与中心对称图形的区别与联系： 中心对称中心对称图形区别（1）是针对两个图形而言的.（2）是指两个图形的（位置）关系.（3）对称点在两个图形上.（4）对称中心在两个图形之间.（1）是针对一个图形而言的.（2）是指具有某种性质的一个图形.（3）对称点在一个图形上.（4）对称中心在图形上.联系（1）都是通过把图形旋转重合来定义的.（2）两者可以相互转化，如果把中心对称的两个图形看成一个整体（一个图形），那么这“一个图形”就是中心对称图形；反过来，如果把一个中心对称图形相互对称的两部分看成两个图形，那么这“两个图形”中心对称知识点二 作中心对称图形的方法中心对称图形的性质：①中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平分；②中心对称的两个图形是全等图形.作中心对称图形的一般步骤（重点）：①作出已知图形各顶点（或决定图形形状的关键点）关于中心的对称点——连接关键点和中心，并延长一倍确定关键的对称点.②把各对称点按已知图形的连接方式依次连接起来，则所得到的图形就是已知图形关于对称中心对称的图形.找对称中心的方法和步骤：对于中心对称图形和关于某一点对称的两个图形，它们的对称中心非常重要，找不对称中心是解决先关问题的关键.由中心对称的特征可知，对称中心为对应点连线的中点或两组相对应点连线的交点，因此找对称中心的步骤如下：方法1：连接两个对应点，取对应点连线的中点，则中点为对称中心.方法2：连接两个对应点，在连接两个对应点，两组对应点连线的交点为对称中心.知识点三 关于原点对称的点的坐标规律两个点关于原点对称时，它们的坐标符号相反，即点P（x，y）关于原点O的对称点P’(-x，-y)1.1、下列图形中，既是轴对称图形，又是中心对称图形的是（  ）A． B． C． D．1.2、四组图形中成中心对称的有(　   　)(A)1组    (B)2组    (C)3组    (D)4组1.3、如图，已知长方形的长为10cm，宽为4cm，则图中阴影部分的面积为（　　）A．20cm2    B．15cm2    C．10cm2    D．25cm2【变式训练1-1】如图案中，既是中心对称图形又是轴对称图形的是（　　）A. B. C. D.【变式训练1-2】如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1;④△ABC与△A1B1C1的面积相等,其中正确的有(　　) A.1个         B. 2个        C. 3个        D.4个【变式训练1-3】如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,若AB=3,BC=4,那么阴影部分的面积为(　　) A.4   B.12        C.6        D.32.1、如图，在小正方形组成的网格中，每个小正方形的边长均为1个单位(1)画出三角形ABC向右平移4个单位所得的三角形A1B1C1．(2)若连接AA1、CC1，则这两条线段之间的关系是_______．(3)画出三角形ABC绕点O逆时针旋转180°所得的三角形A2B2C2． 2.2、如图，在边长为1个单位长度的的小正方形网格中.（1）将先向右平移3个单位长度，再向下平移2个单位长度，作出平移后的；（2）请画出，使和关于点成中心对称；（3）直接写出的面积. 【变式训练2-1】如图，△ABC在平面直角坐标系内，顶点的坐标分别为A（﹣4，4），B（﹣2，5），C（﹣2，1）．（1）将△ABC绕点（0，3）旋转180°，得到△A1B1C1，画出旋转后的△A1B1C1；（2）求（1）中的点C旋转到点C1时，点C经过的路径长（结果保留π）．       3.1、若点P（m，2）与点Q（3，n）关于原点对称，则m，n的值分别为（　　）A．，2 B．3， C．， D．3，23.2、如图,已知△ABC的三个顶点坐标分别为点A(-2,3),B(-6,0),C(-1,0).(1)    将△ABC绕坐标原点O旋转180°,得到△A′B′C′,画出图形,并写出点A的对应点A′的坐标;(2)请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.【变式训练3-1】若P(x，3)与点Q(4，y)关于原点对称，则xy的值是(　　)A．12 B．﹣12 C．64 D．﹣64【变式训练3-2】已知点P(x,y)的坐标满足方程(x+3)2+=0,求点P分别关于x轴、y轴、原点的对称点坐标.          【变式训练3-3】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2),请解答下列问题:(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1的坐标;(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出点A2的坐标;(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出点A3的坐标.4、如图,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE.求证:FD=BE.  【变式训练4-1】如图,在△ABC中,AB=AC,△ABC与△DEC关于点C成中心对称,连接AE,BD.(1)线段AE,BD具有怎样的位置关系和大小关系?说明你的理由.(2)如果△ABC的面积为5 cm2,求四边形ABDE的面积.   1．正方形ABCD在直角坐标系中的位置如图所示，将正方形ABCD绕点A按顺时针方向旋转180°后，C点的坐标是(   )A．(2，0) B．(3，0) C．(2，－1) D．(2，1)2．用一条直线 m 将如图 1 的直角铁皮分成面积相等的两部分．图 2、图 3 分别是甲、乙两同学给出的作法，对于两人的作法判断正确的是（    ）A．甲正确，乙不正确 B．甲不正确，乙正确C．甲、乙都正确 D．甲、乙都不正确3.如图,△ABC和△AB′C′成中心对称,A为对称中心,若∠C=90°,∠B=30°,BC=,则BB′长为　. 4.如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,AB=2,则阴影部分的面积之和为　　. 5.下列图标是由我们熟悉的一些基本数学图形组成的,其中既是轴对称图形又是中心对称图形的是　　.(填序号) 6.如图,在4×4的正方形网格中,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是　　. 7.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为　　. 8．如图，在平面直角坐标系中，四边形OABC是正方形，点C（0，4），D是OA中点，将△CDO以C为旋转中心逆时针旋转90°后，再将得到的三角形平移，使点C与点O重合，写出此时点D的对应点坐标：_____．9．抛物线y＝2x2－4x＋5绕它的坐标原点O旋转180°后的二次函数表达式为________．10.下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影.(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.(请将三个小题依次作答在图①、图②、图③中,均只需画出符合条件的一种情形)     11.如图，在平面直角坐标系中，的三个顶点分别是、、.(1)画出关于点成中心对称的△；平移，若点的对应点的坐标为，画出平移后对应的△；(2)△和△关于某一点成中心对称，则对称中心的坐标为　 　．12.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).(1)求对称中心的坐标.(2)写出顶点B,C,B1,C1的坐标.           1．下列图形中，既是中心对称图形，又是轴对称图形的是（    ）A． B． C． D．2．如图，在平面直角坐标系中，的顶点在第一象限，点、的坐标分别为、，，，直线交轴于点，若与关于点成中心对称，则点的坐标为（  ）A． B． C． D．3．已知点P（a+1，）关于原点的对称点在第四象限，则a的取值范围在数轴上表示正确的是（　　）A． B．C． D．4．国产越野车“BJ40”中，哪个数字或字母既是中心对称图形又是轴对称图形(    )A．    B．    C．4    D．05．已知点A(a＋b，4)与点B(－2，a－b)关于原点对称，则a2－b2等于(    )A.8 B.－8 C.5 D.－56．如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 (   )A．2种 B．3种 C．4种 D．5种7．将点P（-2，3）向右平移3个单位得到点P1，点P2与点P1关于原点对称，则P2的坐标是（    ）A．（-5，-3）    B．（1，-3）    C．（-1，-3）    D．（5，-3）8．在平面直角坐标系中，点A的坐标为（a，3），点B的坐标是（4，b），若点A与点B关于原点O对称，则ab=_____．9．若点（，1）与（﹣2，b）关于原点对称，则=_______．10．在边长为1个单位长度的小正方形组成的网格中，建立如图所示的平面直角坐标系△ABC是格点三角形（顶点在网格线的交点上） （1）先作△ABC关于原点O成中心对称的△A1B1C1，再把△A1B1C1向上平移4个单位长度得到△A2B2C2；（2）△A2B2C2与△ABC是否关于某点成中心对称？若是，直接写出对称中心的坐标；若不是，请说明理由.